Contoh Soal Matriks Jawaban +Pembahasan
Soal No.2 (UN 2009)
Diketahui matriks A =

dan B =

.jika A’ adalah transpose matriks A dan AX = B + A’ maka determinan matriks x adalah …
- 46
- 33
- 27
- -33
- -46
PEMBAHASAN :

Jawaban : D
Soal No.3 (SNMPTN DASAR 2011)
jika A adalah matriks 2×2 yang memenuhi

dan

maka hasil kali adalah …





PEMBAHASAN :

Jawaban : C
Soal No.4 (UN 2009)
Diketahui 3 matriks

.Jika A X B
t – C =

dengan B
t adalah transpose matriks B, maka nilai a dan b masing-masing adalah …
- -1 dan 2
- 1 dan -2
- -1 dan -2
- 2 dan -1
- -2 dan 1
PEMBAHASAN :

Jawaban : A
Soal No.5 (SBMPTN 2014 DASAR)
Jika P =

dan

= 2 P
-1dengan P(-1) menyatakan invers matriks P, maka x+y=….
- 0
- 1
- 2
- 3
- 4
PEMBAHASAN :

Jawaban : C
Soal No.6 (UN 2008)
Diketahui matriks P =

dan Q =

Jika P
-1 adalah invers matriks P dan Q
-1 adalah invers matrik Q. Maka determinan matriks P
-1Q
-1 adalah…
- 223
- 1
- -1
- -10
- -223
PEMBAHASAN :

Jawaban : B
Soal No.7 (SNMPTN 2010 DASAR)
Jika M adalah matriks sehingga  , maka determinan matriks M adalah ……
, maka determinan matriks M adalah ……
- 1
- -1
- 0
- -2
- 2
PEMBAHASAN :

Jawaban : A
Soal No.8 (UN 2004)
Diketahui matriks S =

dan M =

. Jika fungsi f(S+M, S-M) adalah …





PEMBAHASAN :

Jawaban : A
Soal No.9 (SNMPTN 2012 DASAR)
Jika A =

, B =

, dan det (AB) = 12 maka nilai x adalah …
- -6
- -3
- 0
- 3
- 6
PEMBAHASAN :

Jawaban : B
Soal No.10 (EBTANAS 2003)
Nilai x
2 + 2xy + y
2 yang memenuhi persamaan

adalah …
- 1
- 3
- 5
- 7
- 9
PEMBAHASAN :

Jawaban : A
Soal No.11 (SBMPTN 2014 DASAR)
Jika matriks A =

, B =

Dan C =

memenuhi A + B = C
t dengan C
t transpos matriks C maka 2x+3y = …
- 3
- 4
- 5
- 6
- 7
PEMBAHASAN :

Jawaban : C
Soal No.12 (EBTANAS 2000)
Diketahui A =

, B =

dan A
2 = xA + yB. Nilai xy =…
- -4
- -1
- – ½
- 1½
- 2
PEMBAHASAN :

Jawaban : B
Soal No.13 (SNMPTN 2014 DASAR)
Jika

dengan b
2 ≠ 2a
2 maka x + y = ….
- -2
- -1
- 0
- 1
- 2
PEMBAHASAN :

Jawaban : C
Soal No.14 (SNMPTN 2012 DASAR)
Jika AB =

dan det (A) =2 maka det (BA
-1) adalah ….
- 8
- 6
- 4
- 2
- 1
PEMBAHASAN :

Jawaban : D
Soal No.15 (SNMPTN 2009 DASAR)
Matriks A =

mempunyai hubungan dengan matriks B =

. Jika matriks C =

dan matriks D mempunyai hubungan serupa seperti A dengan B maka matriks C + D adalah …..





PEMBAHASAN :

Jawaban : D
Soal No.16 (UM UGM 2004)
Jika I matriks satuan dan matriks A =

sehingga A
2 = pA + ql maka p+q sama dengan ….
- 15
- 10
- 5
- -5
- 10
PEMBAHASAN :

Jawaban : D
Soal No.17
Jika diketahui matriks

Jika P + Q = R’ dan R’ merupakan transpose matriks R, Tentukan nilai x+y!
PEMBAHASAN :
Diketahui:
P + Q = C’

Maka diperoleh:
- 6 + x = 3, maka x = -3
- 3 + x – y = 8, maka 3 + (-3) – y = 8
y = -8
Sehingga diperoleh x + y = -3 + (-8) = -11
Soal No.18
Diketahui matriks A =

dan B =

Tentukan matriks 4AB – BA!
PEMBAHASAN :

Soal No.19
Matrik P =

dan Q =.

Matriks (P – kQ) merupakan matriks singular. Tentukan nilai k
PEMBAHASAN :

Karena Matris (P-kQ) singular maka determinan matriks tersebut bernilai 0
|P – k.Q|= 0
Maka :

(k+1)k = 12
k2 + k = 12
k2 + k – 12 = 0
(k+4)(k-3) = 0
Maka nilai yang memenuhi adalah k = -4 dan k = 3
Soal No.20
Diketahui matriks P =

Q =

, jika nilai deteminannya adalah 4, Tentukan nilai -2x + y – z = 0
PEMBAHASAN :
Menentukan matriks PQ


Diketahui determinannya = 4, maka:

8(-2x+y+z)-0=4
Maka
-2x+y+z = 0,5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , maka determinan matriks M adalah ……
, maka determinan matriks M adalah ……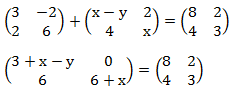
![]()
![]()


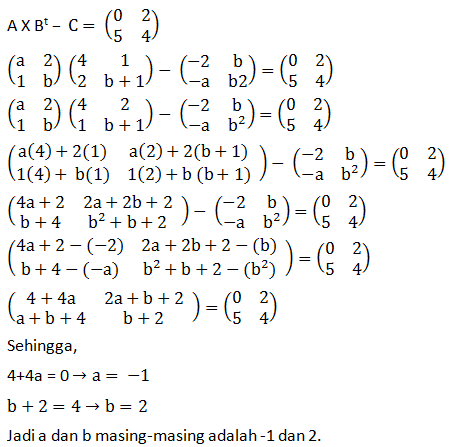


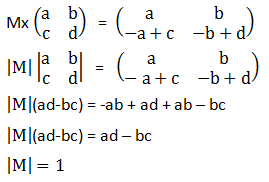
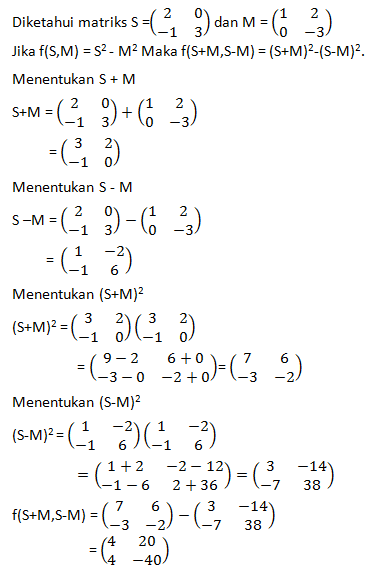


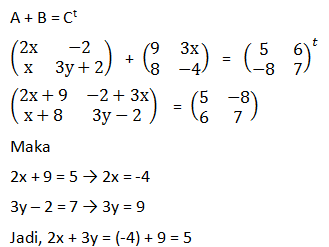
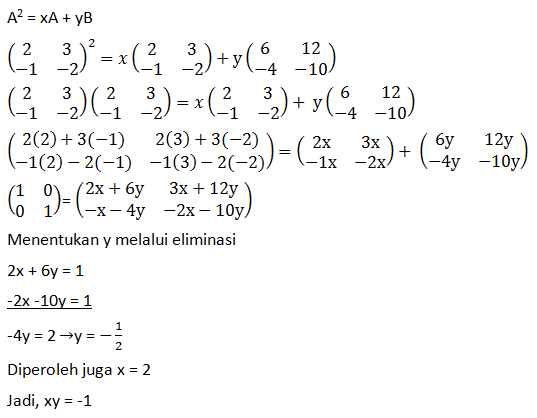



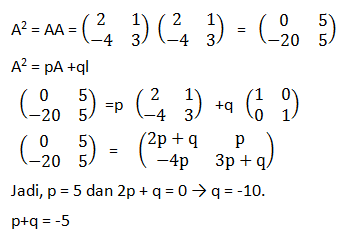
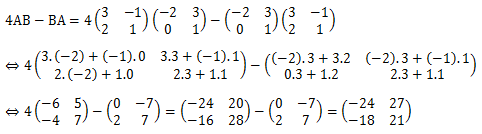

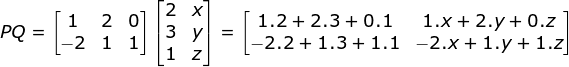

Bagus nih contoh-contoh soal & pembahasannya. 🙂
Sekalian share tulisan saya: “Istilah ‘Matriks’ dalam Matematika berasal dari kata ‘Rahim’ dalam bahasa Latin.”
https://rk-awan.blogspot.com/2019/07/istilah-matrix-berasal-dari-kata-rahim.html