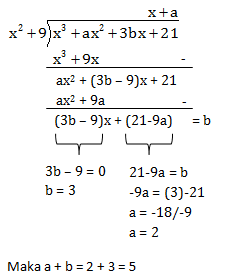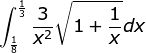Pembahasan Soal SBMPTN Matematika IPA Tahun 2018

Jika periode fungsi f(x) = 2 cos(ax) + a adalah , maka nilai minimum fungsi f adalah….

1. 1
2. 2
3. 4
4. 6
5. 8

PEMBAHASAN :
Diketahui:
f(x) = 2.cos(ax)+a
Periodenya = 
Menentukan nilai a

maka a = 6
f(x) = 2.cos(6x)+6
fungsi akan minimum jika cos 6x = -1
f_min = 2.(-1) + 6 = -2+6 = 4
Jawaban C

DOWNLOAD PEMBAHASAN SOAL SBMPTN MATEMATIKA IPA TAHUN 2018 DALAM BENTUK PDF KLIK DISINI

PEMBAHASAN :

P'(10-a, b+2) = P'(2, -3)
maka nilai a dan b
10-a = 2
a = 8
b+2 = -3
b = -5
Sehingga a + b = 8 + (-5) = 3
Jawaban A

Diketahui kubus ABCD.EFGH dengan panjang rusuk cm. Jika titik P di tengah-tengah AB dan titik Q di tengah-tengah BC, maka jarak antara titik H dengan garis PQ adalah…. cm

1. 
2. 4
3. 
4. 
5. 

PEMBAHASAN :
Jika kubus digambarkan, dimana t adalah jarak titik H ke garis PQ

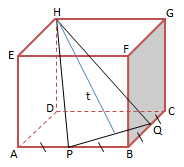
panjang rusuk (r) =
Panjang AP = PB =
Panjang BQ = QC =

Menentukan Panjang HP dan HQ

Menentukan panjang PQ

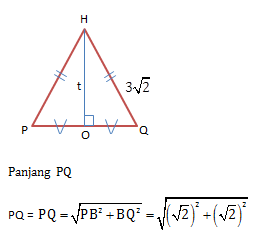
Maka Panjang OQ = 1/2 x 2 = 1

Menentukan Jarak titik H ke garis PQ (t)

Jawaban C

…

PEMBAHASAN :

Jawaban B

PEMBAHASAN :
Menentukan rasio dari persamaan 1
U₃ + U₄ = 9(U₁+U₂)
ar² + ar³ = 9 (a + ar)
ar²(1+r) = 9.a(1+r)
r² = 9
r = ± 3
Menentukan suku pertama (a) dari persamaan kedua
U₁.U₄ = 18.U₂
a.ar³ = 18.ar
ar² = 18
a.9 = 18
a = 18/9 = 2
Maka jumlah 4 suku pertama


Jawaban D

Daerah R dibatasi oleh y = , y = ax2, untuk x ∈ [0,2]. Jika volume benda padat yang didapat dengan memutar R terhadap sumbu x adalah 5π maka a =…

PEMBAHASAN :

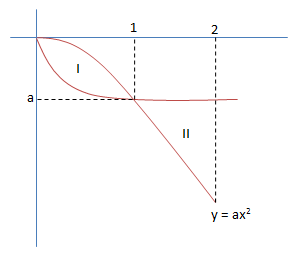
Jika diasumsikan a < 0
Maka volume benda putar:
Volume = V_I + V_II

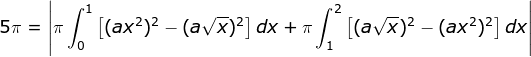
5 = |2a² – 6a² – a²|
5 = |-5a²|
(5-a(-5a²))(5+(-5a²)) = 0
(5+5a²)(5-5a²) = 0
a² = -1
(tidak ada a yang memenuhi)
atau a² = 1
a = 1 atau a = -1
Jawaban E

PEMBAHASAN :

• Menyusun 9 orang berbaris = 9!
• Menyusun 9 orang berbaris dengan Ari & Ira berdampingan = 8 x (2 x 7!) = 2x 8!
• Menyusun 9 orang dengan Ari dan Ira tak berdampingan
  = 9! – 2×8! = 9 x 8! – 2 x 8! = (9-2) x 8! = 7 x 8!

Jawaban A

Jika lingkaran x² + y² + Ax + Ay + A = 0, dengan A > 0, mempunyai jari-jari , maka nilai A adalah…

PEMBAHASAN :
Dari lingkaran
x² + y² − ax − ay + a = 0
Didapat:
A = −a
B = −a
C = a

Menentukan a dari rumus jari-jari lingkaran:



               x 4
a² = 2a² − 4a
a² − 4a = 0
a(a − 4) = 0
a = 0 atau a = 4
Jawaban D

PEMBAHASAN :

Jawaban E

1. 21/4
2. 33/4
3. 52
4. 184
5. 200

PEMBAHASAN :

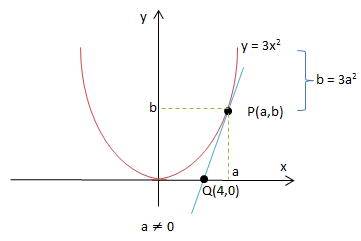
m_pq = y^’_x = a
⇒ m = 6a

⇒ 3a² = 6a²-24a
⇒ 0 = 3a²-24a
⇒ 0 = 3a-24
⇒ 8 = a
b = 3.(8)² = 192
∴ a+b = 8+192 = 200
Jawaban E

Nilai ….

PEMBAHASAN :

Jawaban B

1. 20
2. 21
3. 22
4. 23
5. 24

PEMBAHASAN :
Barisan aritmatika pertama
a₁ = 5
a₂ = 8
maka bedanya (b) = 3
Untuk suku yang ke-100 atau a₁₀₀
a₁₀₀ = a + (n-1)b = 5 + (100-1)3 = 302
sehingga barisan artimatika pertama
a = {5, 8, 11, 14,…, 302} ⇒ U_n = 3n + 2
Barisan aritmatika kedua
b₁ = 3
b₂ = 7
maka bedanya (b) = 4
Untuk suku yang ke-100 atau b₁₀₀
b₁₀₀ = a + (n-1)b = 3 + (100-1)4 = 399
sehingga barisan artimatika kedua
b = {3, 7, 11, 15,…, 399} ⇒ U_n = 4n – 1
Maka
A B = {11, 23, 35,…299}
Barisan aritmatika tersebut memiliki beda (b) sama dengan KPK 3 & 4 = 12
Menentukan banyaknya anggota
U_n = 299 = a + (n-1)b
299 = 11 + (n-1)12
12(n-1) = 299 – 11 = 288

Jawaban Tidak Ada JAwaban

Soal No.13

Himpunan semua bilangan real x pada selang [0, 2π] yang memenuhi 2 – 2cos2x ≤ sin x berbentuk [a,b] ∪ [c,d]. Nilai a+b+c+d adalah….

1. π
2. 2π
3. 3π
4. 4π
5. 5π

PEMBAHASAN :

• 2 – 2.cos²x ≤ √3. sin x
  ⇒ 2(1-cos²x) – √3.sinx ≤ 0⇒ 2.sin²x – √3.sinx ≤ 0⇒ sin x (sinx – ½ √3) ≤ 0

• Batas nilai x pada x ∈ [0 , 2p] :
  sin x = 0                        sin x = ½ √3x = 0 atau x = π           x = π/3 atau x = 2π/3

• Cek Garis Bilangan
  
  nilai yang memenuhi
  0 ≤ x ≤ π/3 ∪ π ≤ x ≤ 2π/3
  ⇒ [0,π/3] ∪ [π, 2π/3] ≡ [a,b] ∴ a + b + c + d = 0 + π/3 + π + 2π/3 = 2π

Jawaban B

Soal No.14

Diketahui f(x) =  dan g(x) = 4^2x-7. Jika (a,b) adalah interval dengan grafik y = f(x) berada di bawah grafik y = g(x), maka nilai a² + b² adalah….

1. 1
2. 5
3. 10
4. 13
5. 17

PEMBAHASAN :
 < 4^{2x – 7}
⇒ x² + x – 12 < 4x – 14

⇒ x² – 3x + 2 < 0
⇒ (x – 1) (x – 2) < 0

1 < x < 2
⇒ (1,2) ≡ (a,b)
∴ a² + b² = 12 + 22 = 5
Jawaban B

Soal No.15

Diketahui dua lingkaran x² + y² = 2 dan x² + y² = 4. Garis l1 menyinggung lingkaran pertama di titik (1,-1). Garis l2 menyinggung lingkaran kedua dan tegak lurus dengan garis l1. Titik potong garis l1 dan l2 adalah….

1. (1+, – 1)
2. (1-, – 1)
3. (1+, +1)
4. (1-, – 2)
5. (1+, + 2)

PEMBAHASAN :

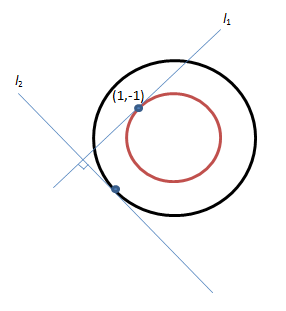
Lingkaran I
L₁ ≡ x² + y² = 2
Titik pusatnya P₁ (0,0)
dengan r₁ =
l1 ≡ x₁.x + y₁.y = 2
⇒ 1.x + (-1).y = 2
⇒ x – y = 2……….persamaan 1
m₁ = – (1/-1) = 1
l₂ : m₁.m₂ = -1
1.m₂ = -1
m₂ = -1
l₂ ≡ y = m₂.x ± r
⇒ y = -1. x ± 2
⇒ y = -x ± 2
⇒ x + y = 2……….. persamaan 2
atau
x + y = – 2
Menentukan titik potong l₁ dan l₂
x – y = 2
x + y = 2
dari kedua persamaan di peroleh
x = 1 +
y = – 1
(1 + , – 1)
Jawaban A

DOWNLOAD PEMBAHASAN SOAL SBMPTN MATEMATIKA IPA TAHUN 2018 DALAM BENTUK PDF KLIK DISINI