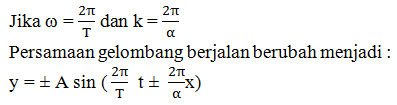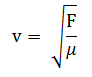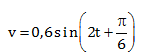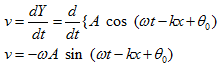Rangkuman, 32 Contoh Soal Gelombang Pembahasan & Jawaban Kelas XI

Pengertian Gelombang

Gelombang adalah getaran yang merambat baik melalui medium maupun tanpa medium.

Jenis-Jenis Gelombang

Berdasarkan arah rambat dan arah getar

dibagi menjadi dua yaitu gelombang transversal dan gelombang longitudinal

Gelombang Transversal

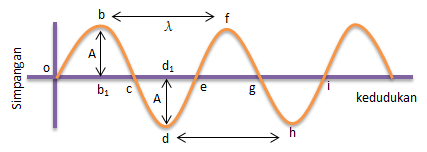
gelombang transversal adalah gelombang yang arah rambatannya tegak lurus terhadap arah rambatannya tegak lurus terhadap perambatannya. Contohnya dalam gelombang pada tali atau gelombang pada air. Istilah yang sering ada pada gelombang transversal diantaranya:

• Puncak gelombang yaitu titik-titik tertinggi pada gelombang (b & f)
• Dasar gelombang yaitu titik-titik terendah pada gelombang ( d & h)
• Bukit gelombang yaitu lengkungan obc atau efg
• Lembah gelombang yaitu cekungan cde atau ghi
• Amplitudo (A) yaitu nilai simpangan terbesar yang dapat dicapai (bb₁ atau dd₁)
• Panjang gelombang (l) yaitu jarak antara dua puncak berurutan (bf) atau jarak antara dua dasar berurutan (dh)
• Periode (T) adalah selang waktu yang diperlukan untuk menempuh dua puncak/ dua dasar yang berurutan

Gelombang Longitudinal

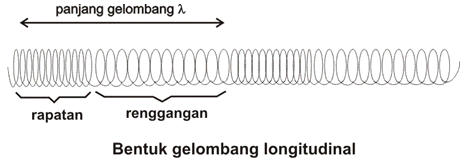
Gelombang longitudinal adalah gelombang yang arah getarnya searah dengan arah perambatannya. Dalam gelombang longitudinal terdapat rengggangan dan rapatan. Contoh dari gelombang longitudinal adalah gelombang pada slinki dan gelombang bunyi.

Panjang gelombang (λ) merupakan jarak antara dua pusat renggangan yang berdekatan atau jarak antara dua pusat rapatan yang berdekatan.

Berdasarkan Mediumnya

Dibagi menjadi dua:

1. gelombang mekanik yaitu gelombang yang membutuhkan media dalam merambat. Contoh gelombang tali dan bunyi.
2. gelombang elektromagnetik yaitu gelombang yang tidak membutuhkan media dalam merambat. Contoh cahaya, gelombang radio dan sinar X.

Berdasarkan Amplitudonya

Dibagi dua :

1. gelombang berjalan dengan amplitudo tetap
2. gelombang stasioner dengan amplitudo berubah sesuai posisinya

Hubungan Panjang Gelombang, Cepat Rambat, Periode, dan Frekuensi.

Hubungannya dirumuskan sebagai berikut:

Keterangan :
v = cepat rambat gelombang (m/s)
λ = panjang gelombang (m)
f = frekuensi (Hertz)
T = periode gelombang (sekon)

Gelombang Berjalan

Simpangan Getar Gelombang

gelombang berjalan di tuliskan dalam persamaan berikut
y = ±A sin (ωt ± kx)
dengan :
y = simpangan gelombang (m)
A = amplitudo gelombang (m)
ω = frekuensi sudut (rad/s)
k = bilangan gelombang
x = jarak titik ke sumber (m)
t = waktu gelombang (s)
A bernilai + jika gelombang permulaannya merambat ke atas
A bernilai – jika gelombang permulaannya merambat kebawah.

Tanda sinus akan bernilai negatif (ωt-kx) jika gelombang permulaannya merambat ke kanan.

Tanda sinus akan bernilai positif (ωt + kx) jika gelombang permulaannya merambat ke kiri.

Kecepatan Partikel dan Percepatan Partikel Pada Gelombang Berjalan.

Kecepatan partikel pada gelombang berjalan dapat dirumuskan sebagai berikut:
v = A ω cos (ωt ± kx)
Percepatan partikel pada gelombang berjalan dapat dirumuskan sebagai berikut:
a = -Aω² sin (ωt ± kx)

Sudut Fase, Fase dan Beda Fase Dari Gelombang Berjalan

sudut fase dari gelombang berjalan di tuliskan dalam persamaan berikut
θ = ωt – kx
Fase gelombang merupakan bagian atau tahapan gelombang dirumuskan sebagai berikut

Keterangan:
j = fase gelombang
t = waktu perjalanan gelombang (s)
T = periode gelombang (s)
x = jarak titik dari sumber (m)
λ = panjang gelombang (m)
ω = frekuensi sudut
k = bilangan gelombang

Gelombang Stasioner

Gelombang stationer merupakan gelombang baru yang dibentuk jika ada dua gelombang berjalandengan frekuensi dan amplitudo sama tetapi arah berbeda bergabung menjadi satu dengan amplitudo yang berubah-ubah. Contohnya pada gelombang tali. Tali dapat digetarkan disalah satu ujungnya dan ujung lain diletakkan pada pemantul. Berdasarkan ujung pemantulnya dapat dibagi dua yaitu ujung terikat dan ujung bebas.

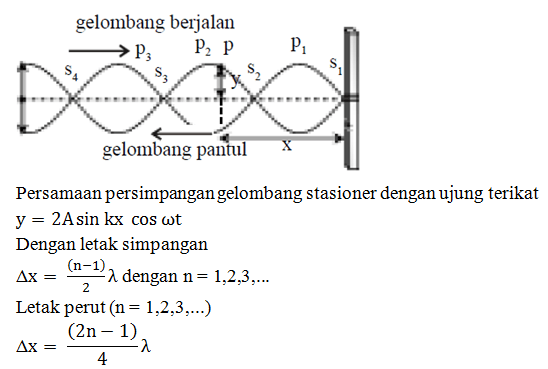
Gelombang Stasioner Dengan Ujung Terikat

Gelombang Stasioner Dengan Ujung Bebas

Hukum Melde

Hukum ini mempelajari tentang besaran-besaran yang mempengaruhi cepat rambat gelombang transversal pada tali. Dari percobaan melde diperoleh rumusan:

keterangan :
v = cepat rambatgelombang
F = gaya tegangan tali
μ = massa persatuan panjang

Sifat-Sifat Gelombang

1. Dapat mengalami pemantulan
2. Dapat menglami pembiasan
3. Dapat mengalami interferensi (perpaduan dua gelombang atau lebih)
4. Dapat mengalami difraksi (melentur melalui lubang kecil)

Contoh Soal Gelombang Pembahasan & Jawaban Kelas XI/11

Soal No.1 (UTBK 2019)

Simpangan suatu gelombang diberikan oleh

dengan x dan y dalam meter serta t dalam sekon. Pernyataan yang benar untuk gelombang tersebut adalah …

1. periode simpangan sebesar π s
2. kecepatan awal simpangan adalah  0,300 m/s
3. frekuensi simpangan π Hz
4. gelombang merambat dipercepat
5. laju perubahan simpangan adalah

PEMBAHASAN :
Berikut persamaan gelombang
Y = 0,3 cos (2t – x + π/6)
Jika dibandingkan persamaan umum gelombang adalah sebagai berikut.
Y = A cos (ωt – kx + θ₀)
Dari kedua persamaan itu diperoleh:

• ω = 2 rad/s
  2πf = 2
  f = 1/π Hz
  periode T = 1/f
  periode T = π detik

• 
  Kecepatan awal di peroleh pada situasi t = 0 dan x = 0
  v = -ωA sin θ
  v = -2. 0,3 sin π/6
  v = – 0,6 sin 30
  v = – 0,3 m/s
  Kecepatan ke arah bawah (ada tanda negatif)

• Laju perubahan simpangan adalah besar dari kecepatan
  v = ωA sin (ωt-kx+π/6)
  _{v = 0,6 sin (2t-x+π/6)}

Jawaban A

Soal No.2 (SBMPTN 2018)

Dua balok kayu kecil A dan B terapung di permukaan danau. Jarak keduanya adalah 150 cm. Ketika gelombang sinusoida menjalar pada permukaan air teramati bahwa pada saat t = 0 detik, balok A berada di puncak, sedangkan balok B berada di lembah. Keduanya dipisahkan satu puncak gelombang. Pada saat t = 1 detik, balok A berada di titik setimbang pertama kali dan sedang bergerak turun. Manakah pernyataan yang benar tentang gelombang pada permukaan air tersebut?

1. Gelombang air memiliki panjang 200 cm
2. Pada saat t = 1 detik, balok B berada di titik setimbang dan sedang bergerak turun.
3. Frekuensi gelombang adalah 0,25 Hz.
4. Amplitudi gelombang adalah 75 cm.
5. Balok A akan kembali berada di puncak pada saat t = 4,5 detik.

PEMBAHASAN :
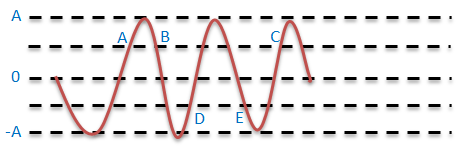
Perhatikan gambar gelombang berikut ini berdasarkan informasi dari soal di atas

Dari gambar di atas diperoleh data:

• jarak antara A dan B adalah 3/2 λ = 150 cm dengan demikian λ = 100 cm
• pada saat t = 1 detik balok A berada di titik setimbang dan sedang bergerak turun, Sedangkan balok B berada di titik setimbang dan sedang bergerak naik
• frekuensi = n/t = = 0,25 Hz
• Balok A akan kembali berada di puncak pada saat t = 4 detik

Jawaban C

Soal No.3 (SBMPTN 2018)

Dua buah benda yang bermassa sama mengalami gerak osilasi seperti pegas dengan frekuensi berbeda. Energi mekanik kedua benda sama. Di antara pernyataan berikut, manakah yang benar?

1. Simpangan maksimum kedua benda berbeda
2. Kecepatan maksimum kedua benda sama
3. Konstanta pegas kedua osilasi berbeda
4. Energi potensial maksimum kedua benda berbeda.

PEMBAHASAN :
Informasi dari soal:
M₁ = M₂
f₁ ≠ f₂
Em₁ = Em₂

1. Pernyataan Y_max1 ≠ Y_max2
   Simpangan maksimum, Y_max disebut amplitudo, A
   Dari persamaan di atas
   Em₁ = Em₂
   ½ K₁A₁² = ½ K₂A₂²
   Jika K = mω² = m4π²f²
   ½ m4π²f₁²A₁² = ½ m4π²f²A₂²
   f₁²A₁² = f₂²A₂²
   f₁A₁ = f₂A₂
                          (Pernyataan 1 benar)
2. Pernyataan a_max1 = a_max2
   a_max1 = ω₁ A₁
   a_max1 = ω₁
   a_max1 = 2π f₁
   a_max1 = 2π f₂ A₂
   a_max1 = ω₂ A₂
   a_max1 = a_max2               (Pernyataan 2 benar)
3. K₁ ≠ K₂
   K = mω² = m4π²f²
   K  ̴ f²
   Karena f₁ ≠ f₂
   Maka K₁ ≠ K₂                    (Pernyataan 3 benar)
4. E_pmaks1 ≠ E_pmaks2
   E_pmaks = E_m
   Karena Em₁ = Em₂
   Maka E_pmaks1 = E_pmaks2  (Pernyataan 4 salah)

Jawaban A

1. (1) dan (2) saja
2. (3) dan (4) saja
3. (2), (3), dan (4)
4. (3),(4) dan (5)
5. (1),(3),(4),dan (5)

PEMBAHASAN :
Ciri-ciri gelombang cahaya diantaranya:

1. Cahaya dapat merambat meskipun dalam ruang hampa
2. Cahaya mengalami pembiasan ketika merambat medium yang memiliki perbedaan kerapatannya
3. Cahaya mengalami refleksi
4. Cahaya mengalami difraksi
5. Cahaya mengalami interferensi

Jawaban : D

1. 1/4
2. 1/2
3. 1
4. 3/2
5. 2

PEMBAHASAN :
Dari titik A ke titik C terdapat dua bukit dan dua lembah. Maka dari titik A ke titik C dikatakan sebagai dua gelombang. Jika dua gelombang dapat dikatakan sebagai dua lamda (panjang gelombang).
Jawaban : E

1. mengenal unsur-unsur suatu bahan
2. mencari jejak sebuah benda
3. memasak makanan dengan cepat
4. membunuh sel kanker
5. mensterilkan peralatan kedokteran

PEMBAHASAN :
Gelombang RADAR dapat di gunakan untuk mencari jejak suatu benda. Selain itu, gelombang RADAR juga dapat di gunakan untuk mendeteksi kecepatan objek dan dimanfaatkan satelit dalam pembuatan peta.
Jawaban : B

1. 3 sekon
2. 4 sekon
3. 8 sekon
4. 33 sekon
5. 50 sekon

PEMBAHASAN :

Jawaban : E

1. 4 m/s dan 4 m
2. 4 m/s dan 2 m
3. 2 m/s dan 4 m
4. 2 m/s dan 2 m
5. 2 m/s dan 1 m

PEMBAHASAN :
1 λ = jarak dua bukit gelombang yang berdekatan, maka:
1λ = 2 meter
λ = 2 meter
Diketahui waktu yang d butuhkan oleh gabus untuk sampai di puncak bukit yaitu satu detik, maka periodenya (T) adalah 2 sekon. Dari data tersebut dapat ditentukan besarnya kecepatan rambat gelombang

maka v dan λ berturut-turut adalah 2 m/s dan 2 meter
Jawaban : D

1. 0,5 m dan 0,5 m/s
2. 0,5 m dan 1 m/s
3. 0,5 m dan 2 m/s
4. 1 m dan 0,5 m/s
5. 2 m dan 1 m/s

PEMBAHASAN :

Jawaban : C

1. y = 0,5 sin 2π (t – 0,5x)
2. y = 0,5 sin π(t – 0,5x)
3. y = 0,5 sinπ (t – x)
4. y = 0,5 sin 2π (t – x/4 )
5. y = 0,5 sin 2π (t – x/6)

PEMBAHASAN :

Jawaban : D

1. 16 m/s
2. 32 m/s
3. 48 m/s
4. 64 m/s
5. 72 m/s

PEMBAHASAN :

Jawaban : A

1. 15 m.s^-1
2. 20 m.s^-1
3. 30 m.s^-1
4. 45 m.s^-1
5. 60 m.s^-1

PEMBAHASAN :

Jawaban : C

PEMBAHASAN :

Jawaban : E

PEMBAHASAN :
Urutan gelombang elektromagnetik berdasarkan frekuensinya dari terkecil hingga terbesar adalah gelombang radio, gelombang tv, gelombang RADAR, sinar infra merah, cahaya tampak, sinar UV, sinar X dan sinar gamma. Maka energi paling besar hingga paling kecil adalah sinar X (3), cahaya tampak (2), Infra merah (1), dan Gelombang TV (4)
Jawaban : D

PEMBAHASAN :

Jawaban : A

1. (1),(2),dan (3)
2. (1) dan (3) saja
3. (2) dan (4) saja
4. (4) saja
5. (1) (2) (3) dan (4)

PEMBAHASAN :
Diketahui persamaaan
y = 0,03 sinπ (2t-0,2x)
y = 0,03 sin(2πt-0,2πx)
Diperoleh data
A = 0,03 meter
Menentukan frekuensi
ω = 2π
2πf = 2π
f = 1 Hz
Menentukan panjang gelombang
k = 0,2π
2π/λ = 0,2 π
λ = 20 m
Maka besarnya cepat rambat gelombang adalah.
v = λf = (20)(1) = 20 m/s
Jawaban : A

1. 8
2. 12
3. 10
4. 4
5. 6

PEMBAHASAN :
Diketahui:
v = 10 m/s
f = 6 Hz
A = 4 cm
S_XY = 20 m

Penyelesaian 1:
Menghitung waktu yang dibutuhkan gelombang untuk merambat dari X ke Y, sebagai berikut:
S_xy = v x t
20 m = 10 m/s x t
t = 2 s

Penyelesaian 2:
Menentukan banyak gelombang (n) yang terjadi sepanjang XY, sebagai berikut:

Maka n = f x t
n = 6 Hz x 2 s
n = 12
Jawaban : B

1. 2 s
2. 1,5 s
3. 3 s
4. 4 s
5. 0,5 s

PEMBAHASAN :
Diketahui:
y = 20 sin π(0,5t – 0,2x) = 20 sin (0,5πt – 0,2πx)
kecepatan sudut = ω = 0,6 π rad/s
Bentuk umum persamaan gelombang berjalan, sebagai berikut:
y = A sin (wt – kx)

y = 20 sin (0,5πt – 0,2πx)

Maka periode (T) gelombang dapat dihitung sebagai berikut:

Jawaban : D

1. 0 cm
2. 3 cm
3. 1 cm
4. 0,5 cm
5. cm

PEMBAHASAN :
Diketahui:
Persamaan gelombang berjalan = y = 0,05 sin π (6t – x)
Jarak titik pengamatan terhadap titik asal = x = 6 cm
Selang waktu titik bergetar = t = 1 detik
x,y dalam cm dan t dalam detik

Maka besar simpangan dapat dihitung sebagai berikut:
y = 0,05 sin π (6t – x)
y = 0,05 sin π (6 . 1 s – 6 cm)
y = 0,05 sin π (0)
y = 0,05 sin 0
y = 0,05 . 0
y = 0
Jawaban : A

1. 15 m/s
2. 18 m/s
3. 20 m/s
4. 23 m/s
5. 24 m/s

PEMBAHASAN :
Bentuk umum persamaan gelombang stasioner yaitu: y = 2 A sin kx cos ωt
Persamaan gelombang stasioner y = 0,2 sin (0,5πx) cos π(12t – 6) meter, maka diperoleh:
2A = 0,2
A = 0,1 meter
k = 0,5π
ω = 12π

Maka kelajuan gelombang pantulnya dapat dihitung sebagai berikut:

Jawaban : E

1. 28,3 cm
2. 31,25 cm
3. 35,1 cm
4. 28,4 cm
5. 30,5 cm

PEMBAHASAN :
Diketahui:
Gelombang stasioner pada tali dengan ujung terikat
l = 50 cm
f = 1/5 Hz = 0,2 Hz
A = 18 cm
V = 5 cm/s
n = 2

Menentukan panjang gelombang sebagai berikut:

Menentukan letak perut ke-2 gelombang dari ujung terikat sebagai berikut:

Maka Δx = l – x
Δx = 50 cm – 18,75 cm
Δx = 31,25 cm
Jawaban : B

1. 8 Hz
2. 10 Hz
3. 14 Hz
4. 12 Hz
5. 6 Hz

PEMBAHASAN :
Diketahui:
Dua buah kawat identik:
m₁ = m₂
l₁ = l₂
f₀ = 600 Hz
f₂ = f₁ + 5%f₁ = f₁ + 0,05f₁ = 1,05f₁

Menentukan frekuensi nada pada dawai kedua setelah tegangannya ditambah sebagai berikut:
Bentuk umum rumus frekuensi nada:

Maka frekuensi layangan yang terjadi dapat dihitung sebagai berikut:
f_layangan = f₀₂ – f₀₁

= (1,02 x 600 Hz) – 600 Hz
= 612 Hz – 600 Hz
= 12 Hz
Jawaban : D

1. 0,4 watt/m²
2. 0,02 watt/m²
3. 1,5 watt/m²
4. 0,5 watt/m²
5. 0,01 watt/m²

PEMBAHASAN :
Diketahui:
P = 100 watt
r = 20 m

Maka intensitas radiasi gelombang bunyi dapat dihitung sebagai berikut:

Jawaban : A

1. 20 dB
2. 30 dB
3. 40 dB
4. 50 dB
5. 60 dB

PEMBAHASAN :
r₁ = 5 meter
TI₁ = 60 dB
r₂ = 50 m

Maka TI₂ dapat dihitung sebagai berikut:

Jawaban : C

1. 1 : 3
2. 2 : 3
3. 1 : 2
4. 1 : 4
5. 4 : 1

PEMBAHASAN :
Jika r_x = 2 x r_Y , maka perbandingan I_Y dan I_X dapat dihitung sebagai berikut:

Jawaban : E

1. 355,5 Hz
2. 264 Hz
3. 333,3 Hz
4. 444,4 Hz
5. 475 Hz

PEMBAHASAN :
Diketahui:
V_s = kecepatan gerak sumber bunyi = 30 m/s
V_p = kecepatan gerak pendengar = 0 m/s (diam)
V_u = kecepatan gelombang bunyi di udara = 240 m/s
f_s =  frekuensi sumber bunyi = 500 Hz

Maka frekuensi yang terdengar oleh orang di pinggir jalan dapat dihitung sebagai berikut:

Catatan:
v_p = 0 m/s dan v_s = menjauhi pendengar (orang di pinggir jalan) sehingga dapat dirumuskan menjadi:

Jawaban : C

1. Tali
2. Slinki
3. Air
4. Udara

PEMBAHASAN :
Gelombang adalah getaran yang merambat melalui medium. Gelombang yang dimaksud yaitu gelombang mekanis, dimana partikelnya tidak ikut merambat, tetapi rambatan yang terjadi adalah rambatan energi. Medium gelombang dapat berupa zat padat, cair, dan gas. Misalnya tali, slinki, air, dan udara. Benar semua maka jawabannya adalah E
Jawaban : E

1. Longitudinal
2. Transversal
3. Diam
4. Berdiri
5. Pegas

PEMBAHASAN :
Banyak jenis gelombang, diantaranya:

• Longitudinal, contohnya: gelombang pegas dan gelombang bunyi
• Transversal, contohnya: gelombang tali, gelombang permukaan air, dan gelombang cahaya
• Diam/ berdiri, contohnya: senar gitar yang dipetik

Jawaban : B

1. Amplitudo gelombang
2. Puncak gelombang
3. Dasar gelombang
4. Periode gelombang
5. Panjang gelombang

PEMBAHASAN :
Besaran dari gelombang terdiri atas:

1. Amplitudo gelombang: simpangan maksimum dari suatu gelombang
2. Puncak gelombang: titik tertinggi dari gelombang
3. Dasar gelombang: titik terendah dari gelombang
4. Periode gelombang: waktu yang dibutuhan untuk menem[uh satu panjang gelombang
5. Panjang gelombang: jarak antara dua puncak atau dua dasar gelombang yang berdekatan

Jawaban : A

1. 5 cm
2. 10 cm
3. 20 cm
4. 30 cm
5. 40 cm

PEMBAHASAN :

Maka panjang gelombang dapat dihitung sebagai berikut:

Jawaban : C

1. 4 m/s
2. 6 m/s
3. 8 m/s
4. 10 m/s
5. 12 m/s

PEMBAHASAN :
Gelombang berjalan dapat dirumuskan secara umum, sebagai berikut:
y = A sin (ωt ± kx),


A = 0,02
ω = 6π
k = π

Maka:
2πf = 6π
f = 3 Hz

v = λ . f
= 2 . 3
= 6 m/s
Jawaban : B

Diketahui persamaan simpangan pada sebuah gelombang tali yaitu . Maka percepatan maksimum gelombang adalah … (x dalam cm dan t dalam sekon).

1. 0,1 p² m/s²
2. 0,6 p² m/s²
3. 0,8 p² m/s²
4. 0,9 p² m/s²
5. 0,5 p² m/s²

PEMBAHASAN :

Jawaban : D