DAFTAR ISI
Rangkuman, Contoh Soal & Pembahasan Vektor Kelas X
Pengertian
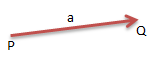
Vektor merupakan besaran yang mempunyai panjang dan arah. Contoh : vektor memiliki titik pangkal P dan titik ujung Q. Sedangkan panjang vektor ![]() dilambangkan dengan
dilambangkan dengan ![]() . Vektor dapat ditulis dengan huruf kecil misalkan
. Vektor dapat ditulis dengan huruf kecil misalkan ![]() ,
, ![]() ,
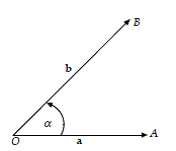
, ![]() . Misalkan pada gambar dibawah ini:
. Misalkan pada gambar dibawah ini:
Maka vektor ![]() dapat ditulis
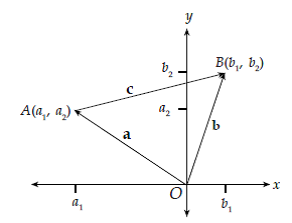
dapat ditulis ![]() . Pada diagram cartesius jika dimisalkan titik A (a1, a2) dan titik B (b1, b2)
. Pada diagram cartesius jika dimisalkan titik A (a1, a2) dan titik B (b1, b2)
Operasi Aljabar Pada Vektor
Penjumlahan dan Pengurangan vektor
Secara geometri penjumlahan vektor ![]() dapat dilakukan dengan dua cara yaitu sebagai berikut
dapat dilakukan dengan dua cara yaitu sebagai berikut
- Cara segitiga
titik pangkal vektor berimpit ruas dengan titik ujung vektor
berimpit ruas dengan titik ujung vektor  . Jumlah vektor
. Jumlah vektor  dan
dan  didapat dengan menarik ruas garis dari titik pangkal vektor
didapat dengan menarik ruas garis dari titik pangkal vektor  ke titik ujung vektor
ke titik ujung vektor  . Ruas garis ini diwakili oleh vektor
. Ruas garis ini diwakili oleh vektor  . Sehingga
. Sehingga  .
.

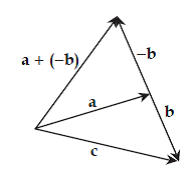
- Aturan jajar genjang
Titik pangkal vektor dan
dan  harus berimpit.
harus berimpit.

Jika vektor dan
dan  di R2
di R2

Jika menggunakan pasangan terurut
 +
+  = (a1 + b1, a2 + b2)
= (a1 + b1, a2 + b2)
 –
–  = (a1 – b1, a2 – b2)
= (a1 – b1, a2 – b2)
Perkalian Vektor
- Perkalian skalar dengan vektor
Jika k skalar tak nol dan vektor = a1 i + a2 j + a3 k maka vektor k
= a1 i + a2 j + a3 k maka vektor k = (ka1, ka2, ka3).
= (ka1, ka2, ka3). - Perkalian skalar dua vektor
Jika vektor = a1 i + a2 j + a3 k dan vektor
= a1 i + a2 j + a3 k dan vektor  = b1 i + b2 j + b3 k maka
= b1 i + b2 j + b3 k maka  .
. = a1 b1 + a2b2 + a3b3
= a1 b1 + a2b2 + a3b3 - Perkalian skalar dua vektor jika membentuk sudut

Jika dan
dan  vektor tak nol dan sudut α diantara vektor
vektor tak nol dan sudut α diantara vektor  dan
dan  . Maka perkalian skalar vektor
. Maka perkalian skalar vektor  dan
dan  adalah . = |
adalah . = | |.|
|.| | cos α
| cos α
Sifat Operasi Aljabar Pada Vektor
Hubungan Vektor Dengan Vektor Lain
Saling Tegak Lurus
Jika tegak lurus antara vektor ![]() dengan vektor
dengan vektor ![]() maka
maka ![]() .
.![]() = 0
= 0
Sejajar
Jika vektor ![]() sejajar dengan vektor
sejajar dengan vektor ![]() kalau
kalau ![]() = β
= β![]() dengan syarat β ≠ 0
dengan syarat β ≠ 0
Jika β > 0 dua vektor tersebut searah
Jika β < 0 dua vektor saling berlawanan arah
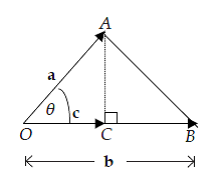
Sudut Dua Vektor
Jika vector (a1, a2, a3) dan vektor (b1, b2, b3) sudut yang dapat dibentuk dari kedua vektor terbut adalah
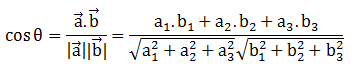
Proyeksi vektor
- Panjang proyeksi vektor a pada vektor b adalah

- Proyeksi vektor a pada vektor b adalah vektor

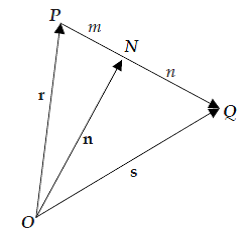
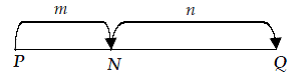
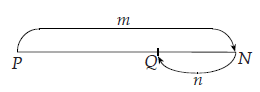
Perbandingan vektor
Perbandingan PN : NQ = m : n terdapat dua jenis, yaitu:
Contoh Soal & Pembahasan Vektor Kelas X/10
- (1, -2, 15)
- (-3, -2, 1)
- (2, 5, 12)
- (3, -2, 10)
- (3, -5, 10)
PEMBAHASAN :

Jawaban : E
PEMBAHASAN :

Jawaban : D
- 6
- 3
- -5
- 1
- -7
PEMBAHASAN :
Syarat vektor segaris yaitu ![]() = k
= k![]()

Perhatikan persamaan (3) dapat diketahui bahwa k = ½
Dengan k = ½
Persamaan (1) → y = 4
Persamaan (2) → x = 2
Maka x + y = 2 + 4 = 6
Jawaban : A
- 5
- 3
- -2
- 6
- -9
PEMBAHASAN :
Perhatikan persamaan berikut:

Persamaan (1) → – 5 = 2k – 3m → – 5 = 2k – 3m
Persamaan (2) kalikan (- 3) → 12 = – 9k – (- (-3)) → 12 = – 9k + 3m
. 7 = -7k
. k = – 1
-5 = 2k – 3m
-5 = 2(-1) – 3m
-5 = -2 – 3m
3m = -2 + 5
3m = 3
m = 1
maka k – m = – 1 – 1 = – 2
Jawaban : C
- 5
- 3
- -2
- 6
- -9
PEMBAHASAN :
Perhatikan persamaan berikut:

Persamaan (1) → – 5 = 2k – 3m → – 5 = 2k – 3m
Persamaan (2) kalikan (- 3) → 12 = – 9k – (- (-3)) → 12 = – 9k + 3m
. 7 = -7k
. k = – 1
-5 = 2k – 3m
-5 = 2(-1) – 3m
-5 = -2 – 3m
3m = -2 + 5
3m = 3
m = 1
maka k – m = – 1 – 1 = – 2
Jawaban : C
PEMBAHASAN :
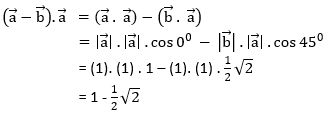
Jawaban : B
- 9 atau -1½
- 3 atau -½
- 1 atau ½
- 9 atau -½
- 3 atau 1
PEMBAHASAN :

Jawaban : A
PEMBAHASAN :

Jawaban : C
PEMBAHASAN :

Jawaban : E
PEMBAHASAN :

Jawaban : D
- 1 dan 2
- 2 dan -3
- -2 dan -3
- 4 dan -1
- -1 dan -3
PEMBAHASAN :
Diketahui:
![]() = (6a, 1, a3)
= (6a, 1, a3)
![]() = (1, 5a2 , 1)
= (1, 5a2 , 1)
![]() .
.![]() = (6a)(1) + (1)(5a2 ) + (a3 )(1)
= (6a)(1) + (1)(5a2 ) + (a3 )(1)
F (a) = 6a + 5a2 + a3
Syarat stasioner, sebagai berikut:
F(a) = 0
6a + 5a2 + a3 = 0 (dibagi a)
6 + 5a + a2 = 0
(a + 3)(a + 2) = 0
Jawaban : C
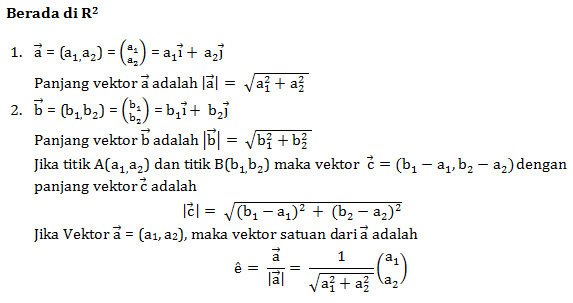
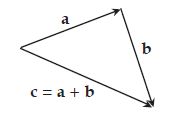
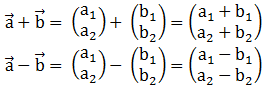







contoh dan soal teknik fisika serta pembahasan sangat membantu untuk saya belajar lebih semangat