DAFTAR ISI
Rangkuman Pertidaksamaan
Pengertian
Pertidaksamaan adalah kalimat matematika terbuka yang menggunakan tanda ketidaksamaan > (lebih dari), < (kurang dari), ≥(lebih dari atau sama dengan), dan ≤ (kurang dari atau sama dengan)
Sifat-sifat Pertidaksamaan
- Jika a dan b bilangan real maka berlaku a > b atau a = b atau a < b
- Jika a > b dan b > c maka a > c
- Jika a > b maka a + c
- Jika a > b dan c > 0 maka ac > bc dan
 >
> 
- Jika a > b dan c < 0 maka ac < bc dan
 <
< 
- Jika m genap dan a > b maka:
- am > bm ,untuk a > 0 dan b > 0
- am < bm ,untuk a < 0 dan b < 0
- Jika n ganjil dan a > b maka an > bn
- Jika a > b maka:
 >
>  untuk a dan b bertanda sama
untuk a dan b bertanda sama <
<  untuk a dan b berbeda tanda
untuk a dan b berbeda tanda
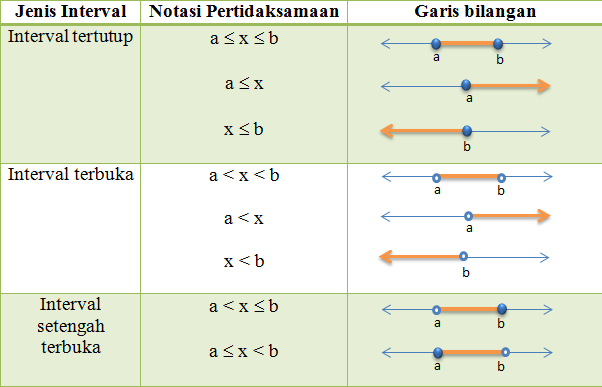
Interval Bilangan
yaitu penyelesaian dari suatu pertidaksamaan
Definit
Jenis Definit
- Definit Positif
Bentuk ax2 + bx + c = 0 dikatakan definit positif jika a > 0 dan D < 0, Jika pertidakasamaan ax2 + bx + c > 0 dalam kondisi definit positif, maka penyelesaiannya adalah semua x Î R. - Definit Negatif
Bentuk ax2 + bx + c = 0 dikatakan definit negatif jika a < 0 dan D < 0, Jika pertidakasamaan ax2 + bx + c < 0 dalam kondisi definit negatif, maka penyelesaiannya adalah semua x Î R.
Sifat Definit
- Untuk f(x) definit positif dan g(x) sembarang
- f(x)g(x) > 0 → g(x) > 0
- f(x)g(x) < 0 → g(x) < 0
 > 0 → g(x) > 0
> 0 → g(x) > 0 < 0 → g(x) < 0
< 0 → g(x) < 0
- Untuk f(x) definit negatif dan g(x) sembarang
- f(x)g(x) > 0 → g(x) < 0
- f(x)g(x) < 0 → g(x) > 0
 > 0 → g(x) < 0
> 0 → g(x) < 0 < 0 → g(x) > 0
< 0 → g(x) > 0
Jenis Pertidaksamaan
- Pertidaksamaan linear
ax + b < 0
ax + b > 0
ax + b ≤ 0
ax + b ≥ 0
Penyelesaian :
Pisahkan variabel x diruas tersendiri terpisah dari konstanta. - Pertidaksamaan Kuadrat
ax2 + bx + c < 0
ax2 + bx + c > 0
ax2 + bx + c ≤ 0
ax2 + bx + c ≥ 0
Penyelesaian :- Jadikan ruas kanan = 0
- Faktorkan ruas kiri.
- Tetapkan nilai-nilai nolnya.
- Tentukan daerah penyelesaian!
- Jika yang ditanya > 0 atau maka daerah penyelesaiannya adalah daerah (+)
- Jika yang ditanya < 0 atau maka daerah penyelesaiannya adalah daerah (-)
- Pertidaksamaan Harga Mutlak
- |f(x)| < a dan a > 0 menjadi bentuk –a < f(x) < a
- |f(x)| > a dan a > 0 menjadi bentuk f(x) < -a atau f(x) > a
- |f(x)| > |g(x)| menjadi bentuk (f(x)+g(x))(f(x) – g(x)) > 0
- a < |f(x)| < b dengan a dan b positif menjadi bentuk a < f(x) < b atau –b < f(x) < -a
- bentuk
 < c dengan c > 0 menjadi bentuk
< c dengan c > 0 menjadi bentuk
|a| < c|b|
|a| < |cb|
(a + cb) (a – cb) < 0
CONTOH SOAL & PEMBAHASAN
Soal No.11 (SNMPTN 2012)
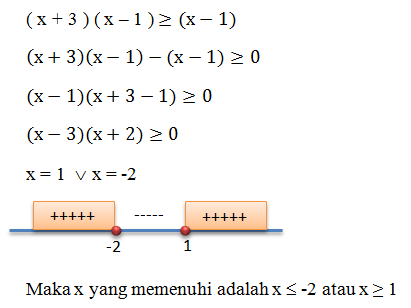
Semua nilai x yang memenuhi (x + 3) (x -1) ≥ (x – 1) adalah ……….
- 1 ≤ x ≤ 3
- x ≤ -2 atau x ≥ 1
- 3 ≤ x ≤ -1
- -2 ≥ x atau x ≥ 3
- -1 ≥ x atau x ≥ 3
Soal No.12 (UN 2002)
Himpunan penyelesaian pertidaksamaan  ≥ 3 adalah …
≥ 3 adalah …
- {x| 1 ≤ x 2}
- {x| 1 ≤ x ≤ 2}
- {x|x < 1}
- {x|x > 2 atau x ≤ 1}
- {x|x > 2 atau x < 1}
Soal No.13 (UN 2012)
Nilai y yang memenuhi  < 1 adalah ……
< 1 adalah ……
- 0 < y ≤ 1
- 0 < y < 1
- y ≤ 0 atau y > 1
- y < 0 atau y ≥ 1
- y < 0 atau y > 1
Soal No.14 (SBMPTN 2014)
semua nilai x yang memenuhi  ≤ 0 adalah …
≤ 0 adalah …
 ≤ 0 adalah …
≤ 0 adalah …- 1/3 < x < 1
- 1/3 ≤ x < 1
- x ≤ 1/3 atau x > 1
- x < 1/3 atau x > 1
- x < 1/3 atau x ≥ 1
Soal No.15 (SNMPTN 2011)
Semua nilai x yang memenuhi  ≤
≤  adalah….
adalah….
 ≤
≤ - x < 2/3 atau x > 2/3
- 1/2 < x < 2/3 atau 2/3 < x < 1
- x ≤ 1/2 atau x ≥ 1
- 1/2 < x < 1
- x < 2/3 atau x > 1
PEMBAHASAN :

Jawaban : C
Soal No.16 (UM UGM 2010)
Himpunan penyelesian dari  ≥ 0
≥ 0
- {x| x ≥ -1}
- {x| x ≥ 4/3
- {x| x ≤ 5/2}
- {x| x ≥ 5/2}
- {x| 4/3 ≤ x ≤ 5/2}
Soal No.17 (SBMPTN 2014)
Semua nilai x yang memenuhi  > 2 adalah….
> 2 adalah….
- -2 ≤ x < -1
- x > 1
- -3/2 ≤ x ≤ -1
- x > 2
- -1 < x < 1
Soal No.18 (SBMPTN 2013)
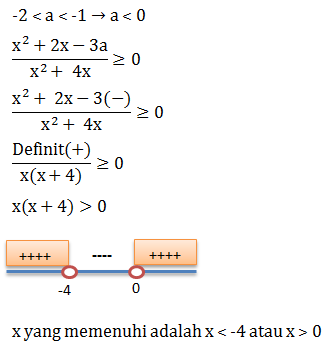
Jika -2 ˂ a ˂ -1, maka semua nilai x yang memenuhi pertidaksamaan  ≥ 0 adalah …
≥ 0 adalah …
- x ˃ -4
- x ˂ -2
- -4 ˂ x ˂ 0
- x ˂ -4 atau x ˃ 0
- x ˂ -2 atau x ˃ 1
Soal No.19 (SBMPTN 2014)
- x < -1/2
- x ≥ -1/2
- x ≥ 2
- x ≤ 2
- x ≤ -1/2 atau x ≥ 2
Soal No.20 (Simak UI 2013)
Himpunan pertidaksamaan dari x2 + 2|x| – 15 ≥ 0 adalah…
- {x ∈ R| x ≤ -3 atau x ≥ 3}
- {x ∈ R| -3 ≤ x ≤ 3}
- {x ∈ R| x ≤ -3}
- {x ∈ R| x ≥ 3}
- {x ∈ R| x > 3}
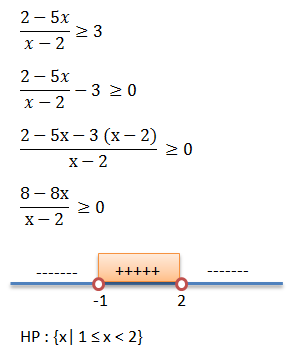

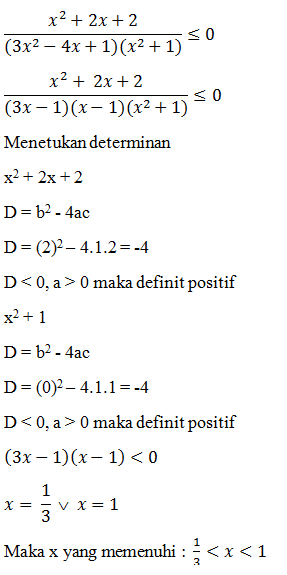


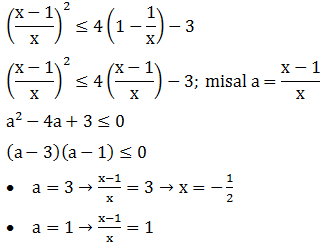
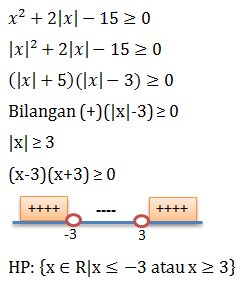
terima kasih, sangat membantu saya 🙂
Terim kasih