Rangkuman Materi Fungsi Kelas 8 SMP

Relasi secara sederhana dapat diartikan sebagai hubungan, hubungan antara daerah asal dan daerah kawan. Sedangkan fungsi adalah relasi yang memasangkan setiap anggota himpunan daerah asal tepat satu ke himpunan daerah kawannya (pemetaan). Setiap relasi belum tentu fungsi, tetapi fungsi pasti merupakan relasi.

Relasi dan fungsi/ pemetaan dapat dibedakan sebagai berikut:

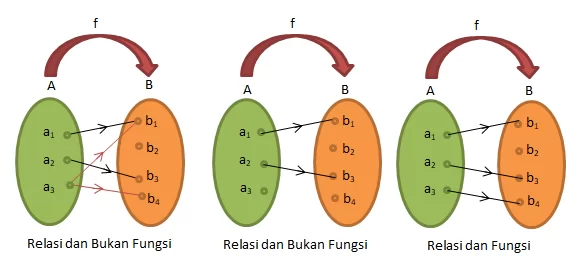
Istilah-istilah daerah pada relasi dan fungsi yaitu:

• Domain: seluruh anggota dari himpunan daerah asal
• Kodomain: seluruh anggota dari himpunan daerah kawan
• Range: daerah hasil dari himpunan daerah asal yang dipasangkan dengan daerah kawan

Relasi

Relasi dari domain A ke kodomain B dapat dituliskan sebagai berikut:

R: A → B

Relasi dapat digambarkan dengan tiga bentuk, yaitu:

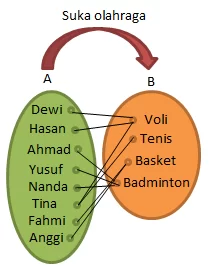
1. Diagram panah
   Diketahui: Murid di suatu kelas menggemari beberapa olah raga sebagai berikut:
   • Dewi dan Hasan menyukai Voli
   • Ahmad, Yusuf, dan Nanda menyukai badminton
   • Tina menyukai Voli dan Tenis
   • Fahmi dan Anggi menyukai Basket

   Misalkan:
   Himpunan A = {Dewi, Hasan, Ahmad, Yusuf, Nanda, Tina, Fahmi, Anggi}
   Himpunan B = {Voli, Tenis, Basket, Badminton}
   

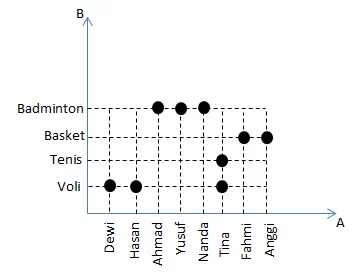
2. Diagram kartesius
   
3. Himpunan pasangan berurutan
   {(Dewi, Voli), (Hasan, Voli), (Tina, Voli), (Tina, Tenis), (Ahmad, Badminton), (Yusuf, Badminton), (Nanda, Badminton), (Fahmi, Basket), (Anggi, Basket)}.
   Apabila x ∈ A dan y ∈ B maka produk kartesius A ke B merupakan himpunan pasangan secara berurutan (x,y). sehingga dapat dituliskan sebagai berikut:
   A x B = {(x,y) | x ∈ A dan y ∈ B}. Contohnya:
   A = {m,n,o}
   B = {2,3}Pembahasan:

   A x B	2	3
   m	(m,2)	(m,3)
   n	(n,2)	(n,3)
   o	(0,2)	(0,3)

   Diperoleh :

   A x B = {(m,2), (m,3), (n,2), (n,3), (o,2), dan (o,3)}

   Banyaknya produk kartesius dapat dihitung dengan rumus sebagai berikut:

   n(A x B) = n(B x A) = n(A) x n(B) , A x B ¹ B x A

Fungsi/Pemetaan

Seperti telah dijelaskan sebelumnya, fungsi adalah relasi yang memasangkan setiap anggota himpunan daerah asal tepat satu ke himpunan daerah kawannya (pemetaan). Misalkan A adalah domain dan B adalah kodomain dapat dikatakan sebagai fungsi/ pemetaan apabila memenuhi syarat-syarat sebagai berikut:

• Setiap anggota himpunan A harus mempunyai pasangan
• Setiap anggota himpunan A hanya dipasangkan dengan satu anggota pada himpunan B

Fungsi/ pemetaan juga dapat dinyatakan dengan diagram panah, diagram kartesius, dan himpunan pasangan berurutan.

Contoh soal fungsi/ pemetaan:
Himpunan A = {1,2,3}
Himpunan B = {-5,-4,-3,-2,-1,0,1,2}

Jika fungsi f: A → B ditentukan dengan f(x) = 4 – 3x. Maka gambarkan dengan diagram panah, diagram kartesius, dan himpunan pasangan berurutan

Pembahasan:
f(x) = 4 – 3x
f(1) = 4 – 3(1) = 1
f(2) = 4 – 3(2) = – 2
f(3) = 4 – 3(3) = – 5

1. Diagram panah
   
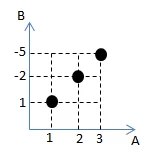
2. Diagram kartesius
   
3. Himpunan pasangan berurutan: {(1,1), (2,-2), (3,-5)}

1. Banyaknya Pemetaan
   Untuk menghitung banyaknya anggota pemetaan, misalkan A = domain dan B = kodomain. Jika banyaknya anggota A = n(A) dan banyaknya anggota B = n(B), maka:
   • Banyaknya pemetaan dari himpunan A ke B = n(B)^n(A)
   • Banyaknya pemetaan dari himpunan B ke A = n(A)^n(B)

   Contoh soal:
   A = {a,b,c} dan B = {1,2,3,4}, hitunglah banyaknya pemetaan dari:

   1. A ke B
   2. B ke A

   Pembahasan:
   A = {a,b,c} → n(A) = 3
   B = {1,2,3,4} → n(B) = 4

   1. Banyaknya pemetaan A ke B = n(B)^n(A) = 4³ = 64
   2. Banyaknya pemetaan B ke A = n(A)^n(B) = 3⁴ = 81

2. Menghitung nilai fungsi
   Untuk menghitung nilai suatu fungsi dapat dilakukan dengan cara mensubstitusikan  nilai ke dalam fungsi f(x).Contoh soal:
   Jika fungsi f(x) = 6x – 3 dengan x = 2, maka nilai fungsi tersebut adalah…Pembahasan:
   f(x) = 6x – 3 ® x = 2
   f(2) = 6(2) – 3 = 9
   Jadi nilai fungsi dari f(x) = 6x – 3 dengan x = 2 adalah 9

Contoh Soal & Pembahasan Fungsi Kelas 8 SMP

1. lebih dari
2. dua kali dari
3. kuadrat dari
4. akar dari

PEMBAHASAN :
Relasi A ke B dapat di jelaskan sebagai berikut:

Dari tabel tersebut relasi A ke B adalah kuadrat dari
Jawaban B

1. {(2, 3), (3, 4), (6, 2), (6, 4), (2, 7), (4, 7)}
2. {(3, 2), (3, 4), (6, 2), (6, 4), (2, 7), (4, 7)}
3. {(3, 2), (3, 4), (6, 2), (6, 4), (7, 2), (7, 4)}
4. {(2, 3), (3, 4), (6, 2), (6, 4), (7, 2), (7, 4)}

PEMBAHASAN :
A x B dapat ditentukan sebagai berikut:

Maka himpunan pasangan berurutannya adalah {(3, 2), (3, 4), (6, 2), (6, 4), (7, 2), (7, 4)}
Jawaban C

1. 1
2. 2
3. -1
4. -2

PEMBAHASAN :
Jika diketahui fungsi:
f(x) = 15x + 4
dimana f(a) = 34, maka :
f(a) = 15.a + 4
34 = 15a + 4
15a = 34 – 4 = 30
a = = 2
Jawaban B

1. 3
2. 9
3. 27
4. 81

PEMBAHASAN :
Jumlah anggota A : n(A) = 4 dan jumlah anggota B : n(B) = 3 maka banyaknya pemetaan yang mungkin adalah 3⁴ = 81
Jawaban D

1. (i)
2. (ii)
3. (iii)
4. (iv)

PEMBAHASAN :
Pemetaan dari A ke B merupakan pemasangan setiap anggota A ke satu anggota B. Sehingga yang termasuk pemetaan adalah (i) yang memasangkan setiap anggota A ke  satu anggota B yaitu hanya pada a saja
Jawaban A

1. {-1, 0, 2, 4, 12}
2. {-1, 3, 7, 11, 15}
3. {1, 4, 7, 9, 13}
4. {-1, 6, 11, 13, 19}

PEMBAHASAN :
Menentukan domain
Anggota {x| -1 ≤ x ≤ 3, x ∈ bilangan bulat} adalah {-1, 0, 1, 2, 3}
Menentukan range dengan substitusi ke fungsi
f(x) = 4x + 3
f(-1) = 4.(-1) + 3 = -1
f(0) = 4.(0) + 3 = 3
f(1) = 4.(1) + 3 = 7
f(2) = 4.(2) + 3 = 11
f(3) = 4.(3) + 3 = 15
Maka range nya adalah {-1, 3, 7, 11, 15}
Jawaban B

1. {a, b, c}
2. {(a, 3), (b, 1), (b, 2)}
3. {1,2,3,4}
4. {(b, 1), (b, 2)}

PEMBAHASAN :
Kodomain merupakan daerah kawan, maka kodomainnya adalah {1, 2, 3, 4}
Jawaban C

PEMBAHASAN :
Menentukan banyaknya produk Cartesius bisa diperoleh dengan mengalikan jumlah anggotanya
n(P x Q) = 9 x 5 = 45
Jawaban C

Jika diketahui f(x) = x + 4 dengan f(16) = 12, maka nilai a adalah….

PEMBAHASAN 
Diketahui fungsi
f(x) = x + 4
f(16) = . 16 + 4 = 12



Jawaban B

1. 30
2. 35
3. 38
4. 40

PEMBAHASAN :
Menentukan tinggi roket setelah 10 detik adalah memasukan waktu ke dalam fungsinya
f(t) = 4t – 2
f(10) = 4.10 – 2 = 40 – 2 = 38 meter
Jawaban C