Rangkuman Materi Kesebangunan Dan Kekongruenan Kelas 9 SMP

Kesebangunan

Kesebangunan adalah dua buah bangun datar dengan panjang sisi-sisi yang bersesuaian mempunyai perbandingan sama besar dan mempunyai sudut-sudut yang bersesuaian sama besar. Kesebangunan di lambangkan dengan symbol notasi ~ . Prinsip kesebangunan dimanfaatkan pada perbesaran foto dan pembuatan model benda.

1. Dua bangun datar yang sebangun
   Sifat-sifat yang dimiliki:
   • Pasangan sisi yang bersesuaian memiliki perbandingan panjang yang sama
   • Besar sudut yang bersesuaian sama besar
     
     Sumber gambar: Buku BSE kelas 9 Matematika

2. Dua segitiga yang sebangun
   Sifat-sifat yang dimiliki:
   • Panjang sisi-sisi yang bersesuaian memiliki perbandingan panjang yang sama
   • Besar sudut yang bersesuaian sama besar
   • Sudut-sudut yang bersesuaian memiliki perbandingan yang sama sehingga sudut yang diapit pada kedua sisinya memiliki besar yang sama
     
     Sumber gambar: Buku BSE kelas 9 Matematika

3. 3. Segitiga istimewa yang sebangun
      • Segitiga siku-siku, memiliki sifat salah satu sudutnya memiliki besar 90⁰
      • Segitiga sama kaki, memiliki sifat dua sisi memiliki panjang yang sama, dua sudutnya sama besar, dan hanya memiliki satu sumbu simetri
      • Segitiga sama sisi, memiliki sifat panjang ketiga sisinya sama besar, tiga buah sudutnya sama besar, dan memiliki tiga sumbu simetri
        

Rumus yang berlaku pada bangun datar  yang sebangun:

Persegi:

Segitiga:

Sedangkan untuk bangun segitiga siku-siku memiliki keistimewaan, maka rumus yang berlaku:

Kekongruenan

Kekongruenan adalah dua buah bangun datar yang memiliki bentuk, ukuran dan besar sudut yang bersesuaian sama besar. Kekongruenan dilambangkan dengan simbol notasi ≅. Prinsip kekongruenan sering dimanfaatkan pada proses pengubinan.

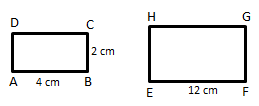
1. Dua bangun datar yang kongruen
   Sifat-sifat yang dimiliki:
   • Kedua bangun memiliki bentuk yang sama
   • Panjang sisi-sisinya sama besar antara dua bangun
   • Contoh gambar dua bangun persegi dan persegi panjang

2. Dua segitiga yang kongruen
   • Ketiga sisi yang bersesuaian berukuran sama besar → sisi-sisi-sisi
   • Dua sisi yang bersesuaian sama besar dan sudut yang diapit oleh kedua sisi ini sama besar → sisi-sudut-sisi
   • Satu sisi yang mengapit dan dua sudut yang saling bersesuaian sama besar → sudut-sisi-sudut
     
     Sumber gambar : Bse Kelas 9 Matematika

Contoh Soal & Pembahasan Kesebangunan & Kekongruenan Bangun Datar Tingkat SMP

1. 2
2. 3
3. 4
4. 5

PEMBAHASAN :
Dari soal dapat diketahui bahwa
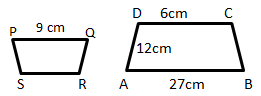
Trapesium PQRS sebanding dengan trapesium ABCD, maka berlaku:

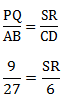
27 SR = 54
SR = 2
Maka, Panjang SR adalah 2 cm.
Jawaban A

1. 4
2. 5
3. 6
4. 7

PEMBAHASAN :
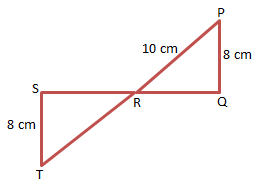
Karena ΔSTR sebanding ΔPQR, maka berlaku

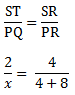
4x = 24
x = 6
Jawaban C

1. 8,6 m
2. 9 m
3. 9,6 m
4. 10 m

PEMBAHASAN :
Jika dimisalkan panjang bayangan tiang 14 meter = x, jika didasarkan pada kesebangunan, maka:

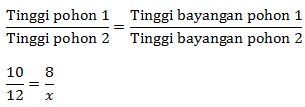
10x = 96
x = 9,6 m
Maka, Panjang bayangan pohon ke 2 adalah 9,6 m.
Jawaban C

1. 6
2. 7
3. 8
4. 5

PEMBAHASAN :
Diketahui ΔABC = ΔCDE karena bersesuaian maka:
ST = PQ = 8 cm
PR = RT = 10cm
RS = QR dapat ditentukan dengan phytagoras

Maka, Panjang RS = QR = 6 cm.
Jawaban A

1. 80 m x 48 m
2. 92 m x 48 m
3. 92 m x 30 m
4. 80 m x 30 m

PEMBAHASAN :
Menentukan ukuran kebun yang sebenarnya

• Panjang = 40 x 200 = 8.000 cm = 80 m
• Lebar = 24 x 200 = 4.800 cm = 48 m

Maka ukuran yang sebenarnya adalah 80 x 48 m
Jawaban A

1. 50⁰
2. 55⁰
3. 60⁰
4. 75⁰

PEMBAHASAN :
Karena kedua layang-layang tersebut sebangun, maka:
∠A = ∠E = 120⁰
∠B  = ∠F = 40⁰
∠C = ∠G = 120⁰
∠D = ∠H = 60⁰
Jawaban C

1. 6 cm
2. 8 cm
3. 9 cm
4. 10 cm

PEMBAHASAN :
Karena sebanding berlaku:

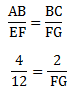
4FG = 24
FG = 6 cm
Maka, Panjang FG adalah 6 cm.
Jawaban A

PEMBAHASAN :
Menentukan panjang QR menggunakan sifat istimewa kesebangunan segitiga siku-siku.

Maka, panjang QR adalah 20 cm.
Jawaban C

PEMBAHASAN 
Menentukan terlebih dahulu lebar sesudah diperbesar, melalui perbandingan:

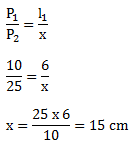
Lebar foto sesudah diperbesar 15 cm.
Maka perbandingan luas foto sebelum dan sesudah diperbesar adalah:

Maka perbandingannya adalah 4 : 25
Jawaban A

1. 180
2. 240
3. 360
4. 420

PEMBAHASAN :
Panjang model (P₁) = 20 cm
Lebar model (l₁) = 12 cm
Panjang sebenarnya (P₂) = 4 m = 400 cm
Menentukan lebar mobil melalui perbandingan

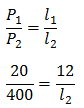
20l₂ = 4800
l₂ = 240 cm
Jawaban B

1. Lingkaran dan oval
2. Persegi dan persegi panjang
3. Dua segitiga sama sisi
4. Segitiga sama sisi dan segitiga siku-siku

PEMBAHASAN :
Dua buah bangun dapat dikatakan sebangun apabila memenuhi syarat sebagai berikut:

• Sudut-sudutnya bersesuaian sama besar
• Sisi-sisi yang bersesuaian memiliki perbandingan ukuran yang sama

Contohnya: lingkaran, segitiga sama sisi, persegi, dan segitiga sama kaki
Jawaban C

1. Sisi-sisi yang bersesuaian memiliki perbandingan ukuran yang sama
2. Sudut-sudutnya bersesuaian sama besar
3. Dua bangun memiliki bentuk dan ukuran yang sama
4. Dua sudut yang bersesuaian memiliki perbandingan sama dan sudut yang diapit kedua sisi tersebut memiliki besar yang sama

PEMBAHASAN :
Dua buah bangun dapat dikatakan sebangun apabila memenuhi syarat sebagai berikut:

• Sudut-sudutnya bersesuaian sama besar
• Sisi-sisi yang bersesuaian memiliki perbandingan ukuran yang sama
• Dua sudut yang bersesuaian memiliki perbandingan sama dan sudut yang diapit kedua sisi tersebut memiliki besar yang sama

Sedangkan dua bangun yang memiliki bentuk dan ukuran sama merupakan syarat kekongruenan.
Jawaban C

1. ∠RPQ dan ∠PQR
2. ∠RPQ dan ∠TSQ
3. ∠PRQ dan ∠TSQ
4. ∠QTS dan ∠PST

PEMBAHASAN :
Sudut yang sehadap adalah sudut yang menghadap ke arah yang sama terhadap garis potong dengan besar sudut yang sama. Pada gambar sudut-sudut yang sehadap adalah:

• ∠RPQ dan ∠TSQ
• ∠PRQ dan ∠STQ

Jawaban B

PEMBAHASAN :
Berdasarkan gambar bahwa ΔLOP ~ ΔLMN sehingga akan berlaku perbandingan sebagai berikut:

Jawaban B

PEMBAHASAN :
Menentukan panjang PR menggunakan sifat istimewa kesebangunan segitiga siku-siku:

Maka panjang PR =
Jawaban A

1. 100
2. 120
3. 130
4. 140

PEMBAHASAN :
ΔABC ~ ΔCDE
∠ACB = 50⁰
∠CBA = 80⁰
∠CAB = ∠CDE = 180⁰ – 50⁰ – 80⁰ = 50⁰
Sehingga ∠ADE = 180⁰ – ∠CDE = 180⁰ – 50⁰ = 130⁰
Jawaban C

1. 5,75
2. 6,75
3. 4,5
4. 5,5

PEMBAHASAN :
AC // DE
ΔABC ~ ΔDBE
AD = 4 cm
BD = 9 cm
CE = 3 cm

Berlaku perbandingan:

Maka nilai x = BE = 6,75 cm
Jawaban B

1. 5
2. 6
3. 7
4. 8

PEMBAHASAN :
PR = 8 cm
QT = 7 cm
ST = 4 cm
QS = 8 cm

ΔPQR ~ ΔTQS akan berlaku perbandingan:

Maka panjang RS = 8 cm
Jawaban D

1. 38
2. 48
3. 52
4. 62

PEMBAHASAN :
Dua bangun jajargenjang yang sebangun memiliki sudut-sudut yang bersesuaian sama besar, maka:
∠B = ∠Q = 132⁰
Sehingga ∠A = 180⁰ – 132⁰ = 48⁰ → α = 48⁰
Jawaban B

1. 8 cm x 6 cm
2. 12 cm x 8 cm
3. 10 cm x 12 cm
4. 8 cm x 4 cm

PEMBAHASAN :
Untuk menghitung hasil perbesarannya sebagai berikut:
Panjang = 4 cm diperbesar 2 kali = 4 cm x 2 = 8 cm
Lebar = 3 cm diperbesar 2 kali = 3 cm x 2 = 6 cm
Maka hasil perbesaran gambar menjadi 8 cm x 6 cm
Jawaban A

1. 5
2. 10
3. 15
4. 20

PEMBAHASAN :
ΔABC ≅ ΔCDE sehingga panjang sisi yang bersesuaian besarnya sama. Maka:
AB = DE = 24 cm
AC = CE = 26 cm

Jawaban B

1. 100
2. 105
3. 110
4. 125

PEMBAHASAN :
∠Q = ∠L = 75⁰
∠P dan ∠S = sudut siku-siku = 90⁰

Jumlah sudut pada bangun trapesium adalah sebesar 360⁰ maka:
∠R = 360⁰ – (90⁰ + 90⁰ + 75⁰ ) = 360⁰ – 255⁰ = 105⁰
Jawaban B

1. Segi empat 10 cm x 10 cm
2. Segi empat 20 cm x 30 cm
3. Segi empat 15 cm x 25 cm
4. Segi empat 24 cm x 26 cm

PEMBAHASAN :
Dua buah bangun dapat dikatakan sebangun apabila memenuhi syarat sebagai berikut:

• Sudut-sudutnya bersesuaian sama besar
• Sisi-sisi yang bersesuaian memiliki perbandingan ukuran yang sama

Pasangan bangun di atas adalah bangun persegi yang memiliki perbandingan ukuran yang sama.
Jawaban A

1. 5,2
2. 3,5
3. 2,5
4. 4

PEMBAHASAN :

Bangun ΔRUV sebangun dengan ΔQUW sehingga berlaku:

Jawaban C

1. 15
2. 21
3. 17
4. 31

PEMBAHASAN :

ΔNQR ~ ΔMQS sehingga berlaku:

Maka panjang NO = NR + OR = 3 + 18 = 21

Jawaban B

1. 30
2. 65
3. 45
4. 25

PEMBAHASAN :
ΔABC ~ ΔEDC sehingga:
∠BAC = ∠DEC = 65⁰
Maka ∠DCE = 180⁰ – (90⁰ + 65⁰ ) = 25⁰
Jawaban D

1. 15
2. 16
3. 17
4. 18

PEMBAHASAN :
Tinggi badan Dewi sebenarnya = 1,5 m = 150 cm
Tinggi badan Deni sebenarnya = 1,2 m = 120 cm
Tinggi badan dewi dilukisan = 20 cm

Maka tinggi badan Deni di lukisan dapat dihitung sebagai berikut:

Jadi tinggi badan Deni di lukisan = 16 cm
Jawaban B

1. ΔPOS dan ΔPOQ
2. ΔROS dan ΔQOR
3. ΔPOS dan ΔQOR
4. ΔROS dan ΔPOS

PEMBAHASAN :
Bangun yang memiliki sifat kekongruenan apabila memiliki bentuk dan ukuran sama. Berdasarkan gambar pasangan segitiga yang memenuhi sifat kongruen adalah ΔROS dan ΔPOS.
Jawaban D

1. 15,2
2. 16,7
3. 13,8
4. 175

PEMBAHASAN :
P_s = 1,8 m = 180 cm
L_s = 1,5 m = 150 cm
P_m = 20 cm
Menghitung lebar model lemari (l_m ) sebagai berikut:

Jawaban B

1. Peta
2. Foto
3. Bayangan benda
4. Pengubinan

PEMBAHASAN :
Prinsip kesebangunan dimanfaatkan pada perbesaran foto, ukuran denah peta, bayangan benda, dan pembuatan model benda. Kesebangunan adalah dua buah bangun datar dengan panjang sisi-sisi yang bersesuaian mempunyai perbandingan sama besar dan mempunyai sudut-sudut yang bersesuaian sama besar, sedangkan prinsip pada proses pengubinan memanfaatkan prinsip kekongruenan, yaitu dua buah bangun datar yang memiliki bentuk, ukuran dan besar sudut yang bersesuaian sama besar.
Jawaban D

1. 18 cm x 28 cm
2. 16 cm x 20 cm
3. 12 cm x 15 cm
4. 16 cm x 24 cm

PEMBAHASAN :
Dengan menghitung nilai dari perbandingannya:

Cek satu persatu perbandingan dari pilihan ganda:

Maka persegi panjang yang sebangun adalah yang berukuran 16 cm x 24 cm.
Jawaban D

1. 9
2. 11
3. 21
4. 31

PEMBAHASAN :
Diketahui:
Tinggi bingkai = 35 cm
Lebar bingkai = 25 cm
Lebar foto = 25 – 2(5) = 15 cm

Tinggi foto dapat dihitung dengan perbandingan sebagai berikut:

Untuk menghitung tinggi bingkai bagian bawah yang tidak tertutup foto (lihat gambar), sebagai berikut:
Tinggi bingkai bagian bawah  = 35 – (5 + 21) = 9
Jawaban A

1. 2,5
2. 2,75
3. 3,75
4. 4

PEMBAHASAN :
Diketahui:
Tinggi antena sebenarnya = 5 m = 500 cm
Tinggi antenna di TV = 20 cm
Lebar antenna di TV = 15 cm

Maka untuk menghitung lebar antenna sebenarnya (x), berlaku perbandingan sebagai berikut:

Jawaban C

1. 10,8
2. 20,8
3. 15,8
4. 12,8

PEMBAHASAN :
Diketahui:
DC = 8 cm
CE = 10 cm
BE = 16 cm
BC = CE + BE = 10 + 16 = 26 cm

Menentukan AC melalui perbandingan

Jawaban B

1. 10
2. 15
3. 20
4. 25

PEMBAHASAN :
Diketahui:
BC = 10 cm
DC = 5 cm
AC = AD + DC

Menentukan AC
Pada segitiga siku-siku berlaku:
BC² = CD x AC
10² = 5 x AC
AC = 20

Menentukan AD
AC = AD + DC
20 = AD + 5
AD = 15
Jawaban B

PEMBAHASAN :
Diketahui:
AC = 20 cm
BC = 10 cm

Jawaban C

PEMBAHASAN :
Diketahui:
Panjang PS = x
Panjang SR = w
Panjang QT = z
Panjang TR = y

ΔPQR~ΔSTR, sehingga berlaku perbandingan sebagai berikut:

Jawaban A

1. 32
2. 44
3. 36
4. 25

PEMBAHASAN :

Jawaban C

1. ∠P dan ∠Q
2. ∠R dan ∠N
3. ∠Q dan ∠L
4. ∠R dan ∠Q

PEMBAHASAN :
Sudut-sudut yang sama nilainya pada bangun segitiga  di atas yaitu:

• ∠P dan ∠Q
• ∠R dan ∠N
• ∠Q dan ∠L

Jawaban D

1. 10
2. 15
3. 18
4. 22

PEMBAHASAN :
ΔABC ≅ ΔADF
AB = AD = 12 cm
DC = 9 cm
DF = AC = AD + DC = 12 + 10 = 22
Maka, panjang DF = 22 cm
Jawaban D

1. 180
2. 240
3. 280
4. 320

PEMBAHASAN :
Diketahui:
Panjang QS = 16 cm
Panjang PS = 8 cm

Untuk menghitung luas DPQR, hitung panjang PR sebagai berikut:
PR = PS + RS
QS² = PS x RS
16² = 8 x RS

Maka PR = PS + RS = 8 + 32 = 40
Sehingga untuk menghitung luas ΔPQR sebagai berikut:

Jawaban D

1. Dua sudut yang bersesuaian sama besar dan satu sisi yang diapit kedua sudut tersebut sama panjang.
2. Panjang sisi-sisi yang bersesuaian memiliki perbandingan yang sama.
3. Sudut-sudut yang bersesuaian sama besar.
4. Panjang sisi-sisi sama besar dengan perbandingan sudut yang berbeda.

PEMBAHASAN :
Dua buah segitiga disebut kongruen apabila memenuhi salah satu syarat berikut ini:

• Sisi-sisi yang bersesuaian sama Panjang (sisi,sisi,sisi)
• Dua sisi yang bersesuaian sama Panjang dan satu sudut yang diapit kedua sisi tersebut sama besar (sisi, sudut, sisi)
• Dua sudut yang bersesuaian sama besar dan satu sisi yang diapit kedua sudut tersebut sama Panjang (sudut, sisi, sudut)

Jawaban A

PEMBAHASAN :
Bangun yang kongruen adalah ketika setiap sisi yang bersesuaian sama Panjang dan setiap sudut yang bersesuaian sama besar. Dua bangun yang kongruen pasti sebangun, tetapi dua bangun yang sebangun belum tentu kongruen.
Jawaban A: tidak sebangun, perbandingan sisi-sisinya tidak sama
Jawaban B: sebangun, semua sudutnya sama besar dan perbandingan sisi-sisinya sama
Jawaban C: sebangun, semua sudutnya sama besar dan perbandingan sisi-sisinya sama
Jawaban D: kongruen, setiap sisi yang bersesuaian sama besar dan setiap sudut yang bersesuaian sama besar
Jawaban D

1.  36 cm
2. 24 cm
3. 18 cm
4. 12 cm

PEMBAHASAN :

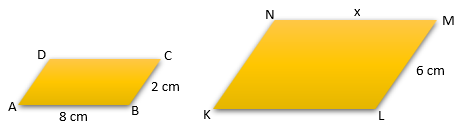
Jajargenjang memiliki sifat sisi-sisi yang berhadapan sama panjang, sehingga AB = CD = 8 cm. Untuk menentukan nilai x dengan menggunakan konsep kesebangunan sebagai berikut:

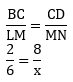
Perkalian silang
2x = 48
x = 24 cm
Jawaban B

1.  20 cm
2. 15 cm
3. 30 cm
4. 25 cm

PEMBAHASAN :

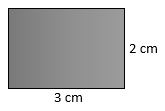
Foto berbentuk persegi panjang dengan ukuran panjang = 2 cm dan lebar = 3 cm. Kemudian diperbesar 2 kali panjang dan 2 kali lebar sebagai berikut:
Panjang = 2 x 2 cm = 4 cm
Lebar = 2 x 3 cm = 6 cm

Maka keliling foto setelah diperbesar adalah:
K = 2 (Panjang + lebar)
= 2 (4 cm + 6 cm)
= 2 (10 cm)
= 20 cm
Jawaban A

1.  8 cm
2. 6 cm
3. 4 cm
4. 2 cm

PEMBAHASAN :
Bangun di atas adalah bangun trapesium.
Dengan menggunakan perbandingan trapesium, maka nilai y dapat dihitung sebagai berikut:


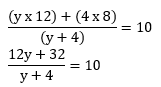
Perkalian silang
12y + 32 = 10 (y + 4)
12y + 32 = 10y + 40
12y – 10 y = 40 – 32
2y = 8
y = 4 cm
Jawaban C

1. 14 m
2. 16 m
3. 18 m
4. 20 m

PEMBAHASAN :
Diketahui:
Tinggi pohon = 5 m
Tinggi bayangan pohon = 7 m
Tinggi tiang = 10 m
Berlaku prinsip kesebangunan sebagai berikut:
Misalkan x = panjang bayangan tiang

5x = 70
x = 14
Maka panjang bayangan tiang adalah 14 m.

Jawaban A

1. 6 cm x 10 cm
2. 9 cm x 12 cm
3. 12 cm x 9 cm
4. 8 cm x 15 cm

PEMBAHASAN :
Diketahui:
Ukuran foto = 3 x 4
Ukuran perbesaran = 3 kali lipatnya
Maka hasil perbesaran dapat dihitung sebagai berikut:
Panjang = 3 cm x 3 = 9 cm
Lebar = 4 cm x 3 = 12 cm
Jadi hasil perbesarannya adalah 9 cm x 12 cm
Jawaban B

1. 60 m x 100 m
2. 40 m x 60 m
3. 50 m x 90 m
4. 60 m x 80 m

PEMBAHASAN :
Diketahui:
Ukuran taman = 24 cm x 32 cm
Skala = 1 : 250
Maka ukuran taman yang sebenarnya dapat dihitung sebagai berikut:
Panjang = 24 cm x 250 = 6.000 cm = 60 m
Lebar = 32 cm x 250 = 8.000 cm = 80 m
Jadi, ukuran taman yang sebenarnya adalah 60 m x 80 m
Jawaban D

1. 20,5 m
2. 25,5 m
3. 22,5 m
4. 24,5 m

PEMBAHASAN :
Diketahui:
Ukuran perahu = 30 cm x 15 cm
Panjang perahu = 45 m
Misalkan x = lebar badan perahu
Maka lebar badan perahu dapat dihitung sebagai berikut:

2x = 45
x = 22,5
Jadi, lebar badan perahu adalah 22,5 m
Jawaban C