Hey..hey kamu kelas XII yang baru naik tingkat. Gimana rasanya jadi anak paling gede di sekolah. Di matematika bab pertama yang kamu pelajari di matematika wajib yaitu dimensi tiga. Disini kita kasih rangkuman materinya, bagian-bagian materi yang wajib kamu kuasai di bab ini. Bukan hanya rangkuman disini juga kamu bisa simak video pembelajaran mengenai dimensi tiga ada 9 part. Lengkap banget. Ga usah bayar-bayar. Gratis buat kalian. Untuk penguasan yang lebih mendalam kita kasih 20 contoh soal & jawaban berikut pembahasannya lengkap! Ok, bagian-bagianya bisa dilihat di daftar isi yah.
DAFTAR ISI
Rangkuman Materi Dimensi Tiga / Geometri Ruang Kelas 12
Kedudukan Titik, Garis, dan Bidang dalam Ruang
- Titik, ditentukan dari letaknya dan tidak memiliki ukuran digambarkan dengan memakai tanda noktah kemudian dibubuhi dengan nama titik itu.

- Garis, hanya memiliki ukuran panjang tidak memiliki ukuran lebar. Sebuah garis bisa dilukiskan sebagian saja disebut wakil garis.

- Bidang, dapat digambarkan sebagian saja disebut wakil bidang. Wakil bidang memiliki panjang dan lebar yang dapat berbentuk persegi atau bujur sangkar, persegi panjang, atau jajar genjang. Nama wakil bidang dituliskan di daerah pojok bidang

Kedudukan Titik Terhadap Garis dan Titik Terhadap Bidang
Kedudukan titik terhadap garis
Kedudukan titik terhadap bidang
Kedudukan garis terhadap garis dan garis terhadap bidang
Kedudukan garis terhadap garis lain
- Dua garis berpotongan

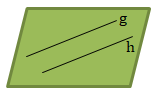
- Dua garis sejajar

- Dua garis berimpit

- Dua garis bersilangan
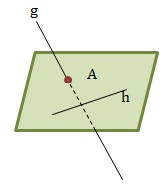
Garis g menembus bidang di titik A, titik A tidak terletak pada garis h

Contoh Soal Dimensi Tiga/Geometri Ruang Kelas 12 Jawaban Dan Pembahasannya

PEMBAHASAN :
Diketahui:
Panjang rusuk = 12cm
Titik tengah AB = P
Titik tengah AD = Q
Titik tengah BC = R
Titik tengah CD = S
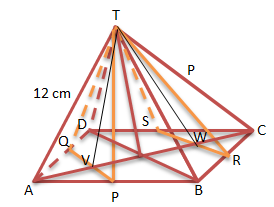
Menentukan sudut sinus antara bidang TPQ dan TRS (sudut VTW)
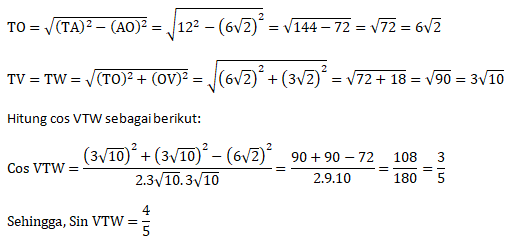
Jawaban : C


- 1


PEMBAHASAN :
Diketahui:
Panjang rusuk = 2cm
Titik tengah AE = P
Titik tengah BF = Q
Titik tengah BC = R
Titik tengah AD = S
Panjang BR = AS = ![]() cm
cm
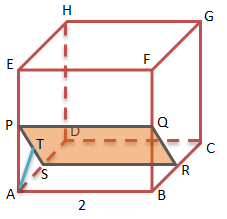
Menentukan jarak A ke bidang PQRS (AT)

Perbandingan luas segitiga pada daerah ΔPAS:
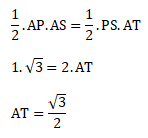
Jawaban : B
PEMBAHASAN :
Diketahui:
Panjang rusuk = 2cm
FP = 2PG
Bidang α = trapesium BDPQ
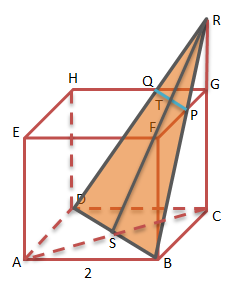
Penyelesaian 1:
Panjang FG = panjang rusuk
FG = 2
FP + PG = 2
2PG + PG = 2
3PG = 2
![]()
Penyelesaian 2:
Perhatikan DBCR dan DPGR
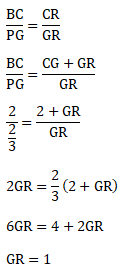
Maka CR = CG + GR = 2 + 1 = 3
Penyelesaian 3:
Perhatikan gambar DSCR di bawah ini:
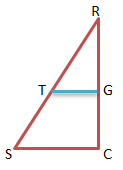
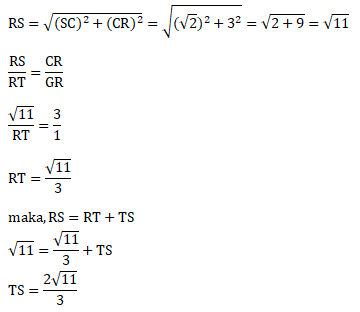
Penyelesaian 4:
Perhatikan DDBR:
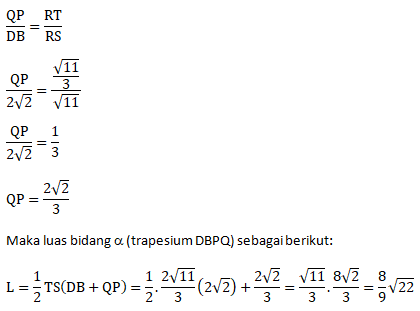
Jawaban : A
PEMBAHASAN :
Diketahui:
BC ⊥ BD
AB ⊥ bidang BCD
BC = BD = ![]()
AB = a cm
CE = ED = ½ CD = a
Perhatikan gambar segitiga berikut:
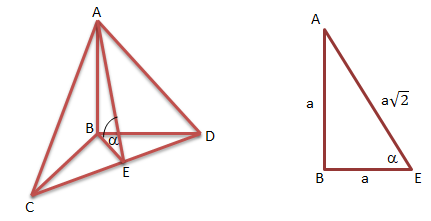
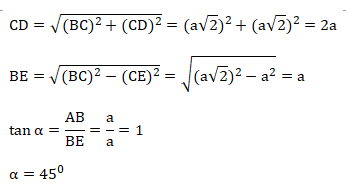
Jawaban : B
PEMBAHASAN :
Diketahui:
∠EBA = ![]()
∠GBC = ![]()
Balok ABCD.EFGH:
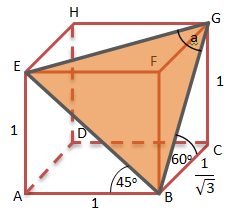
Menentukan BC

Untuk menentukan sin dengan menggunakan aturan cos, sebagai berikut:


Jawaban : A
PEMBAHASAN :
Diketahui:
Titik Q terletak pada sisi TA
TQ : QA = 1 : 2
Titik R terletak di sisi TC
TR : RC = 2 : 1
Titik S terletak di sisi TB
Misalkan, panjang sisinya = 3 cm
Limas segiempat beraturan T.ABCD
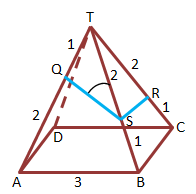
∠T = 600 (sisi tegak berupa segitiga sama sisi)
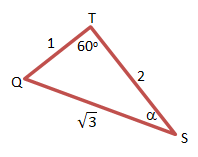
Perhatikan QTS, dengan sudut siku-siku di Q, dengan aturan cos panjang sisi QS adalah

Jawaban : E
PEMBAHASAN :
Kubus ABCD.EFGH
Panjang rusuk = 6 cm
P = titik tengah EH
gambar kubus ABCD.EFGH
AG = diagonal ruang kubus = 6![]() cm
cm
PT = membagi dua garis AG sama Panjang
AT = TG = 3![]() cm
cm
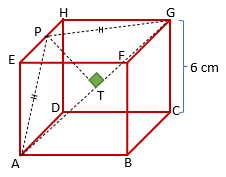
Perhatikan ΔAGP:

ΔAGP adalah segitiga sama kaki karena panjang AP = GP
Menentukan panjang AP, perhatikan ΔAEP dengan siku-siku di E.

Perhatikan ΔAPT:

Jawaban : A
PEMBAHASAN :
Kubus ABCD.EFGH
Panjang rusuk = 12 cm
Perhatikan ΔOGC, yang merupakan segitiga siku-siku di titik C

Panjang diagonal bidang = 12![]() cm
cm
Panjang OC = ½ diagonal bidang
= ½ . 12![]()
= 6![]() cm
cm
Panjang OG:

Maka kosinus sudut antara garis GC dan bidang BDG, sebagai berikut:

Jawaban : D
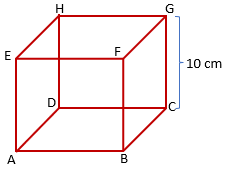
PEMBAHASAN :
Kubus ABCD.EFGH
Panjang rusuk = 10 cm

Perhatikan segitiga ∠AOH
AH = AC = diagonal bidang = 10![]() cm
cm
AO = ½ . AC = ½ . 10![]() = 5
= 5![]() cm
cm
Maka panjang proyeksi AH pada bidang BDHF dapat dihitung sebagai berikut:

Jawaban : B
PEMBAHASAN :
Perhatikan gambar kubus berikut ini!

Pada segitiga BFT siku-siku berada di F
Titik T adalah titik potong diagonal EG dan FH
Panjang BF = 8 cm → Panjang FT = setengah diagonal bidang = 4![]() cm
cm
Maka jarak antara titik B dan titik P dapat dihitung sebagai berikut:

Jawaban : A

- 1
- -1
- ½
- ½


PEMBAHASAN :

Perhatikan ΔTOR:
Siku-siku di O

Perhatikan ΔTOM:
Segitiga sama kaki → Panjang TO = Panjang TM
Gunakan aturan kosinus:

Jawaban : A
- 10 cm
 cm
cm- 3 cm
- 4
 cm
cm  cm
cm
PEMBAHASAN :

Perhatikan ΔQUO:
Siku-siku di Q
Panjang QU = 8 cm
Panjang QO = ½ diagonal bidang = 4![]() cm
cm
Maka jarak titik U ke garis PR sebagai berikut:

Jawaban : E
 cm
cm cm
cm cm
cm cm
cm cm
cm
PEMBAHASAN :

Perhatikan ΔPCG:
Siku-siku di C
Panjang CG = 10 cm
Panjang PC = 5![]() cm
cm
![]()
Perhatikan ΔPKC:


Maka jarak antara titik C dengan bidang BDG = CK sebagai berikut:
CK = sin ∠CPG x CP

Jawaban : D
PEMBAHASAN :

Perhatikan ΔBDT:
BD = DT = p![]() cm
cm
BT = 2p
Gunakan aturan kosinus sebagai berikut:

Maka jarak titik T ke bidang BDHF adalah garis DT = p![]() cm
cm
Jawaban : C
- 16,6
- 2,56
- 20
- 13,2
- 15,5
PEMBAHASAN :

Berlaku rumus luas segitiga dengan panjang sisi a, b, dan c sebagai berikut:
![]()
catatan:
s = ½ x keliling segitiga
Keliling alas = 5 + 3 + 3 = 11 cm
s = ½ x 11 = 5,5 cm
Luas segitiga dapat dihitung sebagai berikut:

Maka volume prisma = luas alas x tinggi
= 4,15 cm x 4 cm
= 16,6 cm3
Jawaban : A
- Persegi
- Trapesium
- Segi lima
- Segi enam beraturan
- Segi empat sembarang
PEMBAHASAN :
Diketahui:
Kubus ABCD.EFGH
Titik a, b, dan c terletak di pertengahan rusuk AE, AB, dan CG

Maka bidang yang terbentuk adalah segi enam beraturan
Jawaban : A
PEMBAHASAN :

Diketahui:
Kubus ABCD.EFGH
Panjang rusuk = p
Diagonal bidang = CH = p![]()
Perhatikan ΔBHC
Jarak C ke bidang diagonal BH = CS
Siku-siku di C
Maka panjang CS adalah sebagai berikut:

Jawaban : B
- 1 : 24
- 2 : 1
- 1 : 15
- 3 : 2
- 5 : 2
PEMBAHASAN :

Misalkan panjang sisi kubus = 1
Maka volume kubus PQRS.TUVW = 1
Tinggi limas A.PQS = ½
Maka volume limas A.PQB dapat dihitung sebagai berikut:

Maka perbandingan antara volume limas A.PQB dan volume kubus PQRS.TUVW

Jawaban : A
PEMBAHASAN :

Panjang rusuk = 6 cm
Proyeksi AH pada bidang BDHF = HP
Siku-siku di D
Maka panjang HP dapat dihitung sebagai berikut:

Jawaban : D
PEMBAHASAN :
Panjang rusuk = 12 cm
A = pertengahan PS
B = pertengahan QR

Perhatikan ΔPQB siku-siku di B:

Perhatikan ΔPAB siku-siku di A:

Jawaban : C
- 0
- 30
- 45
- 60
- 90
PEMBAHASAN :

Diketahui:
Panjang AB = 8 cm
Panjang BC = 8 cm
Panjang AE = 16 cm
Panjang EK = 8 cm

ΔKMH = segitiga sama sisi
EQ = ¼EA
Garis QP // KH
Garis KH = proyeksi garis QP
Panjang KH = MH = 8![]() cm
cm
Maka sudut antara garis PQ dan bidang BDHF = ∠MHL = 300
Jawaban : B
PEMBAHASAN :

Proyeksi ST pada bidang QSWU = SD
Diagonal sisi = 10![]() cm
cm
Panjang WD = ½ diagonal sisi
= ½ x 10![]()
= 5![]() cm
cm
Perhatikan ΔSDW siku-siku di W

Jawaban : D

PEMBAHASAN :
Diketahui:
Limas segitiga beraturan
Panjang LM = MN = LN = 8 cm
Panjang MO = NO = ½ x LM = 4 cm
Panjang LP = 10 cm
Perhatikan ΔLMO siku-siku di O
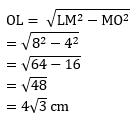
Titik T adalah titik berat ΔLMN sehingga:
![]()
Maka jarak titik P ke OL = PT dapat dihitung sebagai berikut:
Perhatikan ΔLTP siku-siku di T
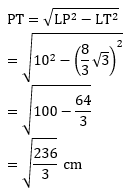
Jawaban : C
PEMBAHASAN :

Diketahui:
Prisma tegak segitiga PQR.STU
PQ = 3 cm
QR = 4 cm
PR = ![]() cm
cm
QS = 10 cm
Berlaku aturan kosinus, perhatikan DPQR sebagai berikut:
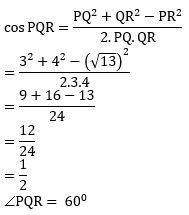
Menghitung luas alas prisma sebagai berikut:
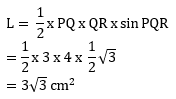
Maka volume prisma = luas alas x tinggi
![]()
Jawaban : E
PEMBAHASAN :

Diketahui:
Kubus PQRS.TUVW
Panjang rusuk = b
X titik tengah PQ
Y titik tengah RS
M adalah titik perpotongan UW dan TV
Jarak titik M ke bidang TXYW = MO
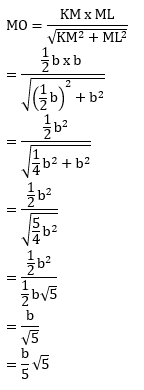
Jawaban : B
- 16
- 6

- 32
- 6

- 10
PEMBAHASAN :

Diketahui:
T.ABCD limas beraturan
Panjang rusuk alas = 10 cm
Panjang rusuk tegak = 16![]() cm
cm
AC = diagonal bidang = 10![]() cm
cm
Perhatikan segitiga sama sisi ACT → AC = CT = TA
Panjang CE = ½ x 16![]() = 8
= 8![]() cm
cm
Perhatikan ΔAEC siku-siku di E, berlaku teorema Phytagoras sebagai berikut:
Jarak A ke TC = AE
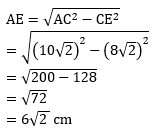
Jawaban : D
PEMBAHASAN :
Diketahui:
Limas beraturan T.ABCD
Panjang rusuk = 8 cm
Diagonal bidang = 8![]() cm
cm
Panjang OC = OA = 4![]() cm
cm
Titik P terletak pada CT
TP : PC = 3 : 1
Panjang TP = 6 cm
Panjang PC = 2 cm
Jarak P ke bidang BDT = PQ
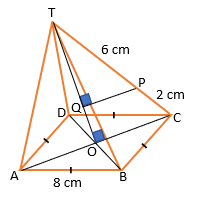
Perhatikan ΔTOC!

Jawaban : E
- 3
 cm
cm - 5
 cm
cm - 5
 cm
cm - 2
 cm
cm - 5
 cm
cm
PEMBAHASAN :
Gambar
Diketahui:
Panjang rusuk = 10 cm
PB = VB → PVB = segitiga sama kaki
B = titik tengah
Panjang TB = ½ x 10 = 5 cm
PV = diagonal ruang kubus = 10![]() cm
cm
Garis AB = membagi PV menjadi dua sama panjang
PA = AV = ½ x 10![]() = 5
= 5![]() cm
cm
Perhatikan segitiga PTB, siku-siku di T
Menentukan panjang PB:

Perhatikan segitiga PBA, siku-siku di T
Menentukan panjang B ke PV atau BA:

Jawaban : B
PEMBAHASAN :
gambar
Diketahui:
Panjang rusuk = 8 cm
DTGC = segitiga siku-siku, dengan siku-siku di C
Diagonal bidang = 8![]() cm
cm
TC = ½ x 8![]() = 4
= 4![]() cm
cm

Maka:

Jawaban : E
PEMBAHASAN :
gambar
Diketahui:
Panjang rusuk = 12 cm
Diagonal bidang = 12![]() cm
cm
Perhatikan ΔPOW!
PW = PR = 12![]() cm
cm
Menentukan panjang PO:
PO = ½ x PR = ½ x 12![]() = 6
= 6![]() cm
cm
Maka panjang proyeksi PW pada bidang QSWU (OW) dapat dihitung sebagai berikut:

Jawaban : A
- 1
- √3
- √2
- 1/2
- 1/4
PEMBAHASAN :
Diketahui:
Balok PQRS.TUVW
PQ = 2QR = 2PT = 2 cm
Perhatikan ΔPSW, siku-siku di S
Maka panjang PW dapat dihitung sebagai berikut:
![]()
Jawaban : C
- Kerucut
- Bola
- Silinder
- Prisma
- Kubus
PEMBAHASAN :
Bola merupakan bangun ruang yang tidak memiliki bidang alas dan titik pojok. Bola terdiri atas titik-titik dalam dimensi tiga yang memiliki jarak sama terhadap pusatnya. Jarak pusat bola ke titik-titik permukaan lingkaran disebut jari-jari bola.
Jawaban : B

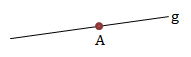









terima kasih,
.
.
.
salam hangat
Membantu sekali
Makasih min ☺️
Terimakasih……..sangat bermanfaat