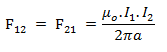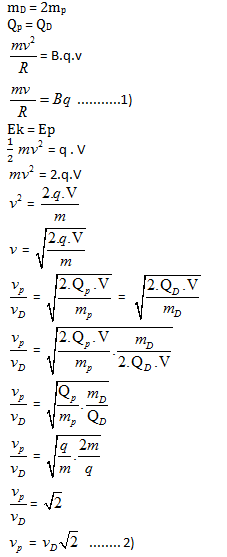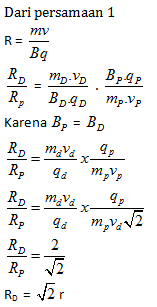DAFTAR ISI
Rangkuman Materi Induksi Magnet Kelas 12
Medan Magnet
Medan magnet merupakan ruang disekitar magnet yang masih dapat dirasakan adanya gaya magnetnya. Pada tahun 1820 seorang ilmuwan Denmark, Hans Christian Oersted (1777-1857) menemukan suatu gejala yang menarik. Saat jarum kompas diletakkan di sekitar kawat berarus ternyata jarum kompas menyimpang. Kemudian disimpulkan bahwa di sekitar kawat berarus timbul medan magnet. Medan magnet oleh kawat berarus inilah yang dinamakan induksi magnet.
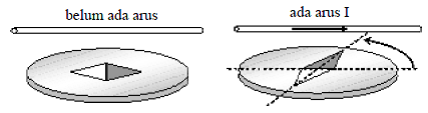
Sumber gambar :Buku Fisika Kelas 3 Sri Handayani
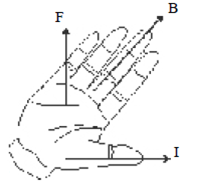
Induksi magnet merupakan besaran vektor arahnya dapat ditentukan dengan menggunakan kaedah tangan kanan

Sumber gambar :Buku Fisika Kelas 3 Sri Handayani
Lambang cros (x) artinya masuk bidang sedangkan dot (•) artinya keluar bidang
Medan Magnet Pada Kawat Lurus Berarus
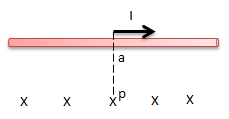
Besarnya medan pada titik P adalah
![]()
Keterangan :
a : Jarak titik p ke kawat
μo : permiabilitas hampa (4π. 10-7 wb/Am)
i = kuat arus listrik (A)
B = Induksi magnetik di titik P (wb/m2)
LIHAT JUGA : Video Pembelajaran Induksi Magnetik
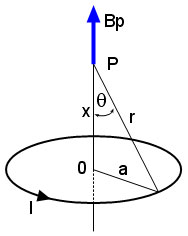
Medan Magnet pada Kawat Melingkar
Pusat Lingkaran Pada Titik O
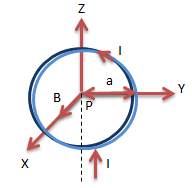
Jika terdiri dari N lilitan maka besar induksi magnet di pusat lingkaran
![]()
Keterangan:
B = Induksi Magnet
N = banyak lilitan.
I = Kuat Arus
a = jarak pusat lingkaran ke kawat
μo : permiabilitas hampa (4π. 10-7 wb/Am)
Medan Magnet Pada Solenoida Berarus
Merupakan kumparan yang dipanjangkan.
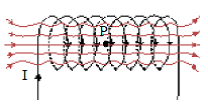
Sumber gambar :Buku Fisika Kelas 3 Sri Handayani
Menentukan Induksi Magnet
Keterangan :
N : Jumlah lilitan
L : Panjang Soleneida(meter)
μo : permiabilitas hampa (4π. 10-7 wb/Am)
i = kuat arus listrik (A)
B = Induksi magnetik di titik P (wb/m2)I = Kuat Arus
Medan Magnet Pada Toroida
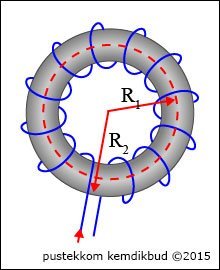
Rumusan Menentukan Induksi Magnet
![]()
Keterangan :
N : Jumlah lilitan
a = rata-rata jari2 dalam dan jari-jari luar toroida dengan satuan meter (m) = (R1 + R2)
μo : permiabilitas hampa (4π. 10-7 wb/Am)
i = kuat arus listrik (A)
B = Induksi magnetik di pusat (wb/m2)
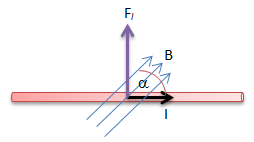
Gaya Lorentz
Gaya yang ditimbulkan oleh medan magnet timbul bila ada interaksi dua medan magnet. Gaya Lorentz antara lain dapat terjadi pada:
- Gaya Lorentz pada kawat Berarus di Dalam Medan Magnet

Aturan tangan kanan digunakan untuk menentukkan arah gaya

Secara matematis dapat dituliskan dengan persamaan:
Fl = B I l sinθ
Keterangan:
Fl = gaya Lorentz (N)
B = besarnya medan magnet (T)
I = Kuat arus yang dialirkan (A)
l = panjang kawat penghantar (m)
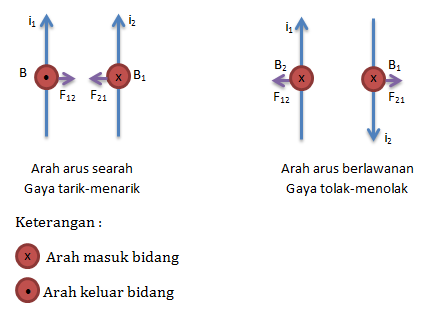
θ = sudut antara arus i dan medan magnet B - Kawat sejajar berarus

Secara matematis besar gaya lorenz pada kawat sejajar dapat ditulis sebagai berikut:

Keterangan :
F12 = F21 = gaya lorentz pada kawat kedua kawat (N)
μo = permeabilitas ruang hampa = 4π.10-7 Wb\Am
I1 = arus pada kawat pertama (A)
I2 = arus pada kawat kedua (A)
I = panjang kawat (m)
a = jarak kedua kawat (m) - Gaya Lorentz Pada Muatan Yang Bergerak Dalam Medan Magnet Muatan bergerak dapat disamakan dengan arus listrik.
Berarti saat ada muatan bergerak dalam medan magnet juga akan timbul gaya Lorentz. Arus listrik adalah muatan yang bergerak dan muatan yang dimaksud adalah muatan positif.

Secara matematis besarnya gaya magnet pada muatan bergerak dapat dinyatakan dengan persamaan berikut
F = B q v sin θKeterangan :
F = gaya lorentz (N)
B = medan magnet (T)
q = besarnya muatan listrik (C)
v = kecepatan muatan (m/s)
θ = sudut antara medan magnet B dan kecepatan muatan v
Adanya sudut antara medan magnet dan kecepatan muatan listrik mengakibatkan muatan memiliki lintasan yang berbeda pada saat berada di dalam medan magnet.- Arah kecepatan muatan positif sejajar dengan medan magnet (θ = 02) maka F = 0

- Arah medan magnet dan kecepatan muatan positif membentuk sudut θ (02 < θ < 10˚)spiral

- Muatan positif tegak lurus dengan medan magnet (θ = 90˚) maka Florenz = fsentripetal sehingga lintasan berbentuk lingkaran

Jari-jari lintasan (R) dapat ditentukan dengan persamaan berikut
 Keterangan:
Keterangan:
R = jari-jari lintasan
m = massa muatan listrik (kg)
B = Induksi Magnet
q = besarnya muatan listrik (C)
v = kecepatan muatan (m/s)
- Arah kecepatan muatan positif sejajar dengan medan magnet (θ = 02) maka F = 0
Contoh Soal Induksi Magnetik & Pembahasan Kelas 12
PEMBAHASAN :
Diketahui:
R1 = 4 cm = 4 x 10-2 m
R2 = 14 cm = 14 x 10-2 m
V2 = 1.5V1
Menentukan perbandingan massa/muatan dapat diperoleh dari rumusan
q.B.R = m.v
![]()
maka perbandingannya
![]()
Karena pada medan magnet yang sama, maka B dapat dicoret
![]()
![]()
PEMBAHASAN :
Diketahui:
m = 6 x 10-25 kg
V = 5 V
q = 1,6 x 10-19 C
B = 4 x 10-2 T
Partikel bergerak memiliki energi kinetik
Ek = q. V = ½.m.v2
maka:
![]()
![]()
Menentukan jari-jari lintasan partikel
dari rumusan:
q. B. R = m. v
![]()
PEMBAHASAN :
Diketahui:
B = 0,4 T
E = 4 x 103 V/m
Menentukan laju partikel
![]()
PEMBAHASAN :
Diketahui:
Jari-jari (a) = 20 cm = 0,2 m
I = 1,2 A
B = 1,2 x 10-3 T
Menentukan banyaknya lilitab pada toroida
![]()
PEMBAHASAN :
Diketahui:
F = 4 x 10-6 N/m
d = 1,5 m
i1 = i2
Menentukan arus listrik kawat
Dari rumusan gaya Lorentz
![]()
karena i1 = i2 ,maka:
![]() , sehingga:
, sehingga:
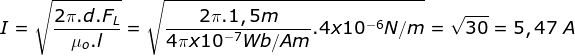
![]()
- 2,4 T
- 3,6 T
- 4,2 T
- 5,6 T
- 6,2 T
PEMBAHASAN :
Diketahui:
A = 40 cm2 = 4 x 10-3 m2
Sudut a = 600
Φ = 7,2 x 10-3 Wb
Maka kuat medan magnet dapat dihitung sebagai berikut:
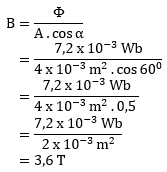
Jawaban : B
- 39,50
- 28,90
- 45,60
- 38,70
- 29,40
PEMBAHASAN :
Diketahui:
A = 160 cm2 = 1,6 x 10-2 m2
B = 0,8 T
Φ = 8 x 10-3 Wb
Maka sudut yang terbentuk antara permukaan benda yang tertembus medan magnet dengan arah garis medan magnet dapat dihitung sebagai berikut:
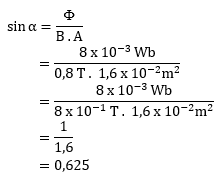
arc sin (0,625) = 38,70
Jawaban : D
- 5,3 A
- 4,8 A
- 6,1 A
- 4,5 A
- 8 A
PEMBAHASAN :
Diketahui:
ΔΦ = 0,6 - 0,2 = 0,4 Wb
t = 5 s
N = 200 lilitan
R = 3 Ω
Menghitung Ggl induksi yang dihasilkan sebagai berikut:
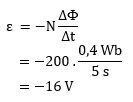
Ket. tanda negatif (-) menunjukkan perubahan fluks induksi yang berlawanan arah dengan fluks magnetik utama.
Maka arus listrik yang mengalir melalui kumparan dapat dihitung sebagai berikut:
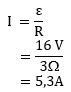
Jawaban : A
- 125 A
- 200 mA
- 125 mA
- 100 A
- 150 mA
PEMBAHASAN :
Diketahui:
A = 150 cm2 = 1,5 x 10-2 m2
R = 6 Ω
N = 500 lilitan
Persamaan perubahan induksi magnetik B = 10-4 sin 1000 t
Menghitung perubahan induksi terhadap waktu sebagai berikut:
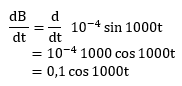
Menghitung kuat arus induksi maksimum pada kumparan dapat dihitung sebagai berikut:
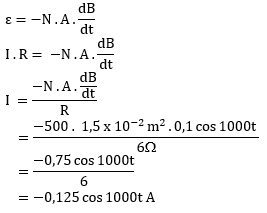
Maka arus listrik mencapai maksimal (Imaks) dengan cos 1000t = 1 dapat dihitung sebagai berikut:
Imaks = - 0,125 A . cos 1000t
= - 0125 . 1
= 0,125 A
= 125 mA
Jawaban : C