Fitur Terbaru!!

Kini kamu bisa bertanya soal yang tidak ada di artikel kami.
Ajukan pernyataan dan dapatkan jawaban dari tim ahli kami.
Untuk bertanya KLIK DISINI

Rangkuman, 50 Contoh Soal & Pembahasan Persamaan Kuadrat

Rangkuman Persamaan Kuadrat

Bentuk Umum Persamaan Kuadrat

Misalkan a, b, c ∈ R dan a ≠ 0, maka persamaan yang terbentuk

ax2 + bx + c = 0

dinamakan persamaan kuadrat dalam peubah x

Akar-akar persamaan kuadrat

Menentukan Akar-akar persamaan kuadrat ada beberapa cara diantaranya :

  1. Memfaktorkan
    Contoh:
    x2 – 6x + 9 = 0
    (x-3) (x-3) = 0
    x – 3 = 0 atau x – 3 = 0
    x = 3
  1. Melengkapkan kuadrat sempurna
    Contoh :
    x2 – 2 x – 2 = 0
    (x2 – 2x + 1) + (-1) – 2 = 0
    (x-1)2 – 3 = 0
    (x-1)2 = 3
    (x-1) = ± √3
    x-1 = √3 atau x -1 = – √3
    x = 1 + √3 atau x = 1 – √3
  1. Menggunakan rumus kuadrat
    per1
    Contoh:
    x2 – 6x + 8 = 0
    a = 1, b = -6, dan c = 8
    per2
    Jadi, akar-akarnya adalah x1 = 2 atau x2 = 4
  2. menggambarkan sketsa grafik fungsi f(x) = ax2 + bx +c

Diskriminan Persamaan Kuadrat

Akar-akar persamaan kuadrat sangat ditentukan oleh nilai diskriminan (D = b² – 4ac) yang membedakan jenis akar-akar persamaan kuadrat menjadi 3, yaitu:

  1. Jika D > 0, maka persamaan kuadrat memiliki dua akar real yang berlainan
    1. Jika D berbentuk kuadrat sempurna, maka kedua akarnya rasional
    2. Jika D tidak berbentuk kuadrat sempurna, maka kedua akarnya irasional
  2. Jika D = 0, maka persamaan kuadrat mempunyai dua akar yang sama (akar kembar), real, dan rasional.
  3. Jika D < 0, maka persamaan kuadrat tidak mempunyai akar real atau kedua akarnya tidak real (imajiner)
  4. Bentuk perluasan untuk akar – akar real:
    1. Kedua akar berkebalikan per3
      • D ≥ 0
      • x1.x2 = 1
    2. Kedua akar berlawanan (x1 = -x2)
      • D > 0
      • x1 + x2 = 0
      • x1.x2 < 0
    3. Kedua akar positif (x1 > 0 ∧ x2 > 0)
      • D ≥ 0
      • x1 + x2 > 0
      • x1.x2 > 0
    4. kedua akar negatif (x1 < 0 ∧ x2 < 0)
      • D ≥ 0
      • x1 + x2 < 0
      • x1.x2 > 0
    5. akar yang berlainan tanda
      • D> 0
      • x1.x2 < 0
    6. kedua akar lebih besar dari bilangan konstan p (x1 > p ∧ x2 > p)
      • D ≥ 0
      • (x1 – p) + (x2 – p) > 0
      • (x1 – p).(x2 – p) > 0
    7. kedua akar lebih kecil dari bilangan konstan q (x1 < q ∧ x2 < q)
      • D ≥ 0
      • ( x1 – q ) + ( x2 – q ) < 0
      • ( x1 – q ) ( x2 – q ) > 0

Sifat Akar

Jika x1 dan x2 adalah akar-akar persamaan kuadrat ax2 + bx + c = 0 dengan D>0, maka berlaku:

  1. per4
  2. per5
  3. per6
  4. Rumus menentukan jumlah dan hasil akar-akar persamaan kuadrat.
    1. Jumlah Kuadrat
      x12 + x22 = (x1 + x2)2 – 2(x1.x2)
    2. Selisih Kuadrat
      x12 – x22 = (x1 + x2) (x1 – x2)
    3. Kuadrat Selisih
      (x1 – x2)2 = (x1 + x2)2 – 4x1.x2
    4. Jumlah Pangkat Tiga
      x13 + x23 = (x1 + x2)3 – 3(x1.x2) – (x1 + x2)
    5. Selisih Pangkat Tiga
      x13 – x23 = (x1 + x2)3 + 3(x1.x2) – (x1 + x2)

menyusun persamaan kuadrat jika diketahui akar-akarnya

  1. Memakai faktor
    (x – x1)(x – x2) = 0
  2. Memakai rumus jumlah dan hasil kali akar-akar
    x2 – ( x1 + x2)x + (x1.x2) = 0

CONTOH SOAL & PEMBAHASAN

Soal No.1 (SBMPTN 2014)
Jika a dan b adalah akar-akar persamaan kuadrat x2 + x – 3 = 0 , maka nilai 2a2 + b2 + a …..
  1. 10
  2. 9
  3. 7
  4. 6
  5. 4

PEMBAHASAN :
a merupakan akar-akar persamaan maka :
a2 + a – 3 =0
a2 = 3-a
2a2 = 6-2a
b juga merupakan akar-akar persamaan maka :
b2 + b – 3 = 0
b2 = 3-b
Sehingga 2a2 + b2 + a
= (6-2a)+(3-b)+a
=9-(ɑ+b)
=9-(-1) = 10
Jawaban : A

Soal No.2 (UN 2014)
Akar-akar persamaan x2 + (p-1)x – 18 = 0 adalah α dan β. Jika α + 2β = 0 dan p≥0 maka nilai p=…
  1. 0
  2. 1
  3. 2
  4. 3
  5. 4

PEMBAHASAN :
per7
Jawaban : E

Soal No.3 (SBMPTN 2014)
Akar-akar persamaan x2+(p+1)x+8 = 0 adalah α dan β. Jika α = ½ β dan α,β positif. Maka nilai p=…
  1. 8
  2. 7
  3. 6
  4. -7
  5. -8

PEMBAHASAN :
per8
Jawaban : D

Soal No.4 (SBMPTN 2014)
Diketahui m dan n akar-akar persamaan ax2+bx+c=0. Jika m + 2 dan n+2 akar-akar persamaan kuadrat ax2+qx+r = 0, maka q+r =…
  1. c + 3b
  2. c – b + 4a
  3. c – b
  4. c – b + 8a
  5. c + 3b + 8a

PEMBAHASAN :
per9
Jawaban : C

Soal No.5 (UN 2002)
Persamaan (2m-4)x2+ 5x+2=0 mempunya akar-akar real berkebalikan maka nilai m=….
  1. -3
  2. – 1/3
  3. 1/3
  4. 3
  5. 6

PEMBAHASAN :
per10

Jawaban : D

Soal No.6 (SBMPTN 2014)
Persamaan kuadrat 2x2-px+1 = 0 dengan p > 0, mempunyai akar-akar. Jika x2-5x+q =0 mempunyai akar-akar per11Maka q – p =……..
  1. -2
  2. -½
  3. ½
  4. 1
  5. 2

PEMBAHASAN :
per12
Jawaban : D

Soal No.7 (UN 2000)
Akar-akar persamaan 2x2 + 2px – q2 = 0 adalah p dan q, p – q = 6, nilai pq =….
  1. 6
  2. -2
  3. -4
  4. -6
  5. -8

PEMBAHASAN :
per13
Jawaban : E

Soal No.8 (SBMPTN 2014)
Jika p dan q merupakan akar akar persamaan kuadrat x2 – (a + 1)x + (- a- 5/2 )= 0. Maka nilai minimum p2 + q2 adalah …..
  1. 5/2
  2. 2
  3. 1
  4. 1/2
  5. 0

PEMBAHASAN :
x2 – ( a + 1 ) x + (-a- 5/2 )= 0
p2 + q2 = ( p + q )2 – 2pq
(a + 1)2 – 2. (-a – 5/2)
a2 + 2a + 1 + 2a + 5
a2 + 4a + 6
Syarat minimum f’( x )= 0
2a + 4 = 0
a = -2
Maka , nilai minimum p2 + q2 adalah
(-2)2 + 4 ( -2) + 6 = 2
Jawaban : B

Soal No.9 (UN 2012)
Persamaan kuadrat x2 + 4px + 4 = 0 mempunyai akar-akar x1 dan x2. Jika x1x22 + x12x2=32, maka nilai p =….
  1. -4
  2. -2
  3. 2
  4. 4
  5. 8

PEMBAHASAN :
x2+ 4px +4=0
x1 + x2= -4p
x1.x2 = 4
x1 x22 +x12 x2 = 32
x1 .x2 (x1 + x2) =32
4 (-4p) = 32
p = -2
Jawaban : B

Soal No.10 (SNMPTN 2010)
Persamaan kuadrat yang mempunyai akar-akar a dan b sehingga per14 adalah …
  1. x2-10x+7 =0
  2. x2+7x+10=0
  3. x2+7x-10=0
  4. x2-7x+10=0
  5. x2-7x-10=0

PEMBAHASAN :
per15
Jawaban : D

Soal No.11 (UN 2012)
Akar-akar persamaan kuadrat x2 +ax -4 = 0 adalah p dan q. Jika p2 -2pq + q2 = 8a, maka nilai a =…
  1. -8
  2. -4
  3. 4
  4. 6
  5. 8

PEMBAHASAN :
per16
Jawaban : C

Soal No.12 (SBMPTN 2014)
Jika x1 dan x2 adalah akar-akar persamaan kuadrat x2 – x – 3 = 0, maka persamaan kuadrat yang akar-akarnya x12+x22 dan 2x1+ 2x2 adalah …
  1. x2-x+9 = 0
  2. x2+x+9 = 0
  3. x2-9x-14 = 0
  4. x2+9x+14 = 0
  5. x2-9x+14 = 0

PEMBAHASAN :
x2 – x – 3 = 0
x1 + x2=1
x1.x2 = -3
x12+x22 = ( x1+x2)2 -2 x1 x2 =1-2(-3) = 7
2x1+2x2 = 2(x1+x2) = 2(1)=2
Maka, persamaan kuadrat baru :
x2 – (7+2)x + (7.2) = 0
x2 – 9x + 14 = 0
Jawaban : E

Soal No.13 (UN 2014)
Akar-akar persamaan kuadrat x2 + (p-3)x +4 = 0 adalah x1 dan x2 . Jika x12 +x22 = p-5 nilai p yang memenuhi adalah….
  1. p = -6 atau p =1
  2. p =-1 atau p =6
  3. p = 1 atau p = 6
  4. p = -6atau p = -1
  5. p = 6 atau p = 2

PEMBAHASAN :
x2 + (p-3)x +4 = 0
x1 +x2 = -(p-3)
x1.x2 = 4
x12 +x22 = p – 5
(x1+x2)2 – 2x1x2 = p – 5
(3-p)2 -2.4 = p-5
p2 – 6p +9 -8 = p-5
p2 -7p + 6 = 0
(p – 1)(p – 6)
p=1 v p=6
Jadi, nilai p =1 atau p = 6
Jawaban : C

Soal No.14 (UN 2012)
Persamaan kuadrat x2 +(m-1)x – 5 = 0 mempunyai akar-akar x1 dan x2. Jika x12 + x22 – 2x1x2 = 8m, maka nilai m…
  1. -3 atau -7
  2. 3 atau 7
  3. 3 atau -7
  4. 6 atau 14
  5. -6 atau -14

PEMBAHASAN :
x2 +(m-1)x-5=0
x12 + x22 – 2x1x2 = 8m
(x1+x2)2 – 4x1 x2 = 8m
(1-m)2 -4(-5) = 8m
m2 – 2m + 1 + 20 = 8m
m2 – 10m + 21 = 0
(m-7)(m-3)=0
m = 7 atau m = 3
Maka, m yang memenuhi adalah 3 dan 7
Jawaban : B

Soal No.15 (UN 2005)
x1 dan x2 adalah akar-akar persamaan kuadrat 3x2 – x -5 = 0. Persamaan kuadrat baru yang akar-akarnya 3x1+1 dan 3x2+1 adalah….
  1. x2 + x – 15 = 0
  2. x2 – x + 15 = 0
  3. x2 + 3x + 13 = 0
  4. x2 – 3x + 13 = 0
  5. x2 – 3x – 13 = 0

PEMBAHASAN :
per17
Jawaban : E

Soal No.16 (UN 2009)
Akar-akar persamaan x12 + x22 adalah α dan β. Persamaan kuadrat baru yang akar-akarnya per18 adalah …
  1. 4x2 + 17x + 4 = 0
  2. 4x2 – 17 + 4 = 0
  3. 4x2 + 17x – 4 = 0
  4. 9x2 + 22x – 9 = 0
  5. 9x2 – 22x – 9 = 0

PEMBAHASAN :
per19
Jawaban : A

Soal No.17 (UN 2001)
Akar-akar persamaan kuadrat x2 + 6x – 12 = 0 adalah x1 dan x2. Persamaan kuadrat baru yang akar-akarnya per20 dan x1 x2 adalah..
  1. x2 + 9x – 18 = 0
  2. x2 – 21x – 18 = 0
  3. x2 + 21x + 36 = 0
  4. 2x2 + 21x – 36 = 0
  5. 2x2 + 21x – 18 = 0

PEMBAHASAN :
per21
Jawaban : D

Soal No.18 (UN 2013)
Salah satu nilai p yang menyebabkan persamaan kuadrat 2x2+(p+1)x+8=0 memiliki akar kembar adalah…
  1. -8
  2. -7
  3. 6
  4. 7
  5. 9

PEMBAHASAN :
Memiliki akar kembar berarti D = 0
b2 – 4ac = 0
(p + 1)2 – 4.2.8 = 0
p2 + 2p + 1 – 64 = 0
p2 + 2p – 63 = 0
(p+9)(p – 7) = 0
p = -9 atau p = 7
Jawaban : D

Soal No.19 (UN 2012)
Persamaan kuadrat x2 + (m-2)x + 2m – 4 = 0 mempunyai akar-akar real, maka m yang memenuhi adalah..
  1. m ≤ 2 atau m ≥ 10
  2. m ≤ -10 atau m ≥ -2
  3. m < 2 atau m > 10
  4. 2 < m < 10
  5. -10 < m < -2

PEMBAHASAN :
per22
Jawaban : A

Soal No.20 (UN 2013)
Agar persamaan kuadrat 4x2 – (p-3)x + 1 = 0 mempunyai dua akar tidak nyata, maka nilai p yang memenuhi adalah …
  1. -1 < p < 7
  2. -7 < p < 1
  3. 1 < p <7
  4. p < -1 atau p > 7
  5. p < 1 atau p > 7

PEMBAHASAN :
Mempunyai dua akar tidak nyata berarti D<0
b2 – 4ac < 0
(-(p-3))2 – 4.4.1 < 0
p2 – 6p+ 9 – 16<0
p2 – 6p – 7 <0
(p-7)(p+1)<0
p = 7 atau p=-1
per23
Jawaban : A

Soal No.21 (UN 2003)
Persamaan kuadrat (k+2)x2 – (2k-1)x + k -1 = 0 mempunyai akar-akar nyata dan sama. Jumlah kedua akar persamaan tersebut adalah …
  1. 9/8
  2. 8/9
  3. 5/2
  4. 2/5
  5. 1/5

PEMBAHASAN :
per24
Jawaban : D

Soal No.22
Diketahui salah satu akar persamaan px2 + 3x – 20 = 0 adalah 4, maka akar yang lain adalah …
  1. – 4
  2. – 10
  3. 2
  4. ½
  5. 10

PEMBAHASAN :
px2 + 3x – 20 = 0 → x = 4
16p + 12 – 20 = 0
16p = 8
p =

Persamaan baru dengan p = ½ sebagai berikut:
½ x2 + 3x – 20 = 0
Kalikan 2 persamaan di atas, menjadi:
x2 + 6x – 40 = 0
(x + 10)(x – 4) = 0
x1 = – 10
x2 = 4
Jawaban : B

Soal No.23
Diketahui 3 adalah satu-satunya akar persamaan kuadrat x2 + px + q = 0. Maka nilai p – q = …
  1. 0
  2. -3
  3. 10
  4. -5
  5. 1

PEMBAHASAN :
x2 + px + q = 0
Kalikan 3 persamaan kuadrat di atas, sebagai berikut:
x2 + 3px + 3q = 0
Persamaan kuadrat yang akarnya 3 adalah (x – 3)2 = 0 → x2 – 6x + 9
Maka nilai p dan q dapat dihitung sebagai berikut:
3px = – 6x
3p = – 6
p = – 2
3q = 9
q = 3
p – q = -2 – 3 = – 5
Jawaban : D

Soal No.24
  1. 1
  2. ½
  3. 0
  4. – ½
  5. -1

PEMBAHASAN :
1 – = -x → kalikan dengan -x
-x + 12 = x2
x2 + x – 12 = 0
(x + 4)(x – 3) = 0
Nilai x yang memenuhi adalah – 4 dan 3
x = -4 →
x = 3 → = 1
Jawaban : A

Soal No.25
Akar-akar persamaan kuadrat x2 – px – 4 = 0 adalah a dan b. jika a2 – 2ab + b2 = 8p, maka nilai p adalah …
  1. 0
  2. 2
  3. -1
  4. 4
  5. 8

PEMBAHASAN :
x2 – px – 4 = 0
a = 1 , b = – p , c = – 4
a2 – 2ab + b2 = 8p
(a – b)2 = 8p

D = 8p
b2 – 4(a)(c) = 8p
(- p)2 – 4(1)(- 4) = 8p
p2  + 16 = 8p
p2 – 8p + 16 = 0
(p – 4)2 = 0
p = 4
Jawaban : D

Soal No.26
Diketahui akar-akar persamaan x2 + (p – 2)x – 4p = 0 berkebalikan, maka nilai p adalah …

PEMBAHASAN :
x2 + (p – 2)x – 4p = 0
a = 1 , b = p – 2 , c = – 4p

x1 . x2 = 1

Jawaban : B

Soal No.27
Diketahui (p + 3) dan (p – 3) merupakan akar-akar persamaan x2 – 8x – q = 0, maka nilai q = …
  1. 8
  2. – 4
  3. 5
  4. – 8
  5. 7

PEMBAHASAN :
x2 – 8x – q = 0 → a = 1, b = – 8, c = – q
(p + 3) + (p – 3) =
2p =
p = 4
(p + 3)(p – 3) =
(4 + 3)(4 – 3) =
q = 7
Jawaban : E

Soal No.28
Persamaan kuadrat x2 – ax + 3a = 0 memiliki akar-akar x1 dan x2 . jika 2x1 + x2 = 1, maka nilai a2  = …
  1. -1
  2. 3
  3. – ½
  4. 0
  5. 1

PEMBAHASAN :
x2 – ax + 3a = 0
a = 1, b = – a, c = 3a
2x1 + x2 = 1
x1 + x2 =
2x1 + x2 = 1
x1 + x2 = a   –
x1 = 1 – a

Substitusikan persamaan di atas, sebagai berikut:
2x1 + x2 = 1
2(1 – a) + x2 = 1
2 – 2a + x2 = 1
x2 = 2a – 1
x1 . x2 = (1 – a)(2a – 1)

3a = 2a – 1 – 2a2 + a
2a2 = – 1
a2 = – ½
Jawaban : C

Soal No.29
Persamaan kuadrat x2 – ax + a = 0 dengan a > 0 yang memiliki akar-akar x1 dan x2 . Jika x12 + x22 = 24, maka a = …
  1. 2
  2. – 8
  3. 4
  4. 6
  5. -10

PEMBAHASAN :
x2 – ax + a = 0
x1 + x2 = a
x1 . x2 = a

x12 + x22 = 24
(x1 + x2 )2 – 2x1 . x2 = 24
a2 – 2a = 24
a2 – 2a – 24 = 0
(a – 6)(a + 4) = 0
Maka a yang memenuhi adalah 6
Jawaban : D

Soal No.30
Jika a dan b adalah akar-akar persamaan kuadrat x2 + 2x + (p – 10) = 0. Untuk a2 – b2  = 24, maka nilai p = …
  1. 144
  2. 24
  3. 10
  4. 25
  5. 100

PEMBAHASAN :
x2 + 2x + (p – 10) = 0
a = 1, b = 2, c = p -10
a2 – b2  = 24
(a + b)(a – b) = 24

44 – 4p = 144
-4p = 100
p = – 25
Jawaban : D

Soal No.31
Diketahui p dan q adalah akar-akar persamaan x2 – x – 2 = 0. Maka nilai dari (p2 – p – 4)(q2 – q + 4) adalah …
  1. 10
  2. -8
  3. -12
  4. 4
  5. 6

PEMBAHASAN :
x2 – x – 2 = 0 → (p2 – p – 2) = 0
p2 – p = 2
(p2 – p – 4)(q2 – q + 4)
= (2 – 4)(2 + 4)
= (-2)(6)
= – 12
Jawaban : C

Soal No.32
Diketahui suatu halaman  berbentuk persegi panjang akan dibangun sebuah kolam renang berbentuk persegi panjang dengan luas 96 m2 . Selisih panjang dan lebar kolam adalah 4 m dan di sekeliling kolam renang dibuat jalan selebar 1 m. Maka luas jalan tersebut adalah … m2 .
  1. 21
  2. 96
  3. 84
  4. 124
  5. 92

PEMBAHASAN :

x . y = 96
x – y = 4
x = 4 + y
(4 + y) (y) = 96
y2 + 4y – 96 = 0
(y – 8)(y + 12) = 0
yang memenuhi y = 8 → x = 12
p = x + 1 = 12 + 1 = 13 m
l = y + 1 = 8 + 1 = 9 m

Maka:
Luas jalan = (p . l) – (x . y)
= (13 . 9) – 96
= 117 – 96
= 21 m2
Jawaban : A

Soal No.33
Jika persamaan kuadrat x2 + (α – 2)x + 4= 0 memiliki akar kembar. Maka nilai α yang memenuhi adalah …
  1. 3 dan – 2
  2. – 4 dan 5
  3. 2 dan 3
  4. – 1 dan – 4
  5. – 2 dan 6

PEMBAHASAN :
x2 + (α – 2)x + 4 = 0
a = 1 , b = (α – 2) , c = 4
Syarat memiliki akar kembar yaitu:
D = 0
b2 – 4.a.c = 0
(α – 2)2 – 4(1)(4) = 0
α2 – 4α + 4 – 16 = 0
α2 – 4α – 12 = 0
(α + 2)(α – 6) = 0
Maka nilai α yang memenuhi adalah -2 dan 6
Jawaban : E

Soal No.34
Persamaan kuadrat x2 + (p – 4)x + 16 = 0 memiliki akar-akar yang real. Maka nilai p yang memenuhi adalah …
  1. p ≤ 4 atau p ≥ – 12
  2. p ≥ – 3 atau p ≥ 15
  3. p ≤ – 5 atau p ≤ – 10
  4. p ≤ – 4 atau p ≥ 12
  5. p ≤ – 2 atau p ≥ 2

PEMBAHASAN :
x2 + (p – 4)x + 16 = 0
a = 1 , b = (p – 4) , c = 16
Syarat memiliki akar-akar yang real yaitu:
D ≥ 0
b2 – 4.a.c ≥ 0
(p – 4)2 – 4(1)(16) ≥ 0
P2 – 8p + 16 – 64 ≥ 0
P2 – 8p – 48 ≥ 0
(p – 12)(p + 4) ≥ 0

Maka nilai p yang memenuhi adalah p ≤ – 4 atau p ≥ 12
Jawaban : D

Soal No.35
Jika persamaan kuadrat x2 + 2px + (p2 – 3p) = 0 memiliki dua akar positif. Maka konstanta p yang memenuhi adalah …
  1. p > 3
  2. p < 0
  3. p < – 3
  4. 0 < p < 3
  5. 3 > p > 0

PEMBAHASAN :
x2 + 2px + (p2 – 3p) = 0
a = 1 , b = 2p , c = (p2 – 3p)
Syarat memiliki dua akar positif yaitu:
D ≥ 0
b2 – 4.a.c ≥ 0
(2p)2 – 4(1)( p2 – 3p) ≥ 0
4p2 – 4p2 + 12p ≥ 0
12p ≥ 0
p ≥ 0
x1 + x2 > 0
(p2 – 3p) > 0
x1 . x2 > 0
(p2 – 3p) > 0
p(p – 3) > 0
p < 0 atau p > 3
Maka konstanta p yang memenuhi adalah p > 3
Jawaban : A

Soal No.36
Diketahui a dan b adalah akar-akar real persamaan . Maka nilai a.b = …
  1. 2 dan 3
  2. – 2
  3. – 3
  4. – 2 dan – 3
  5. 0

PEMBAHASAN :

Misalkan: (x2 + x) = m

m(m + 1) = 6
m2 + m – 6 = 0
(m + 3)(m – 2) = 0
Untuk m = 2
x2 + x = 2
x2 + x – 2 = 0
a . b = – 2 → D > 0 (akarnya real)
Untuk m = -3
x2 + x = – 3
x2 + x + 3 = 0
a . b = 3 → D < 0 (akarnya tidak real)
Maka nilai a .b dengan akar yang real adalah – 2
Jawaban : B

Soal No.37
Persamaan kuadrat x2 + px + (p – 1) = 0 memiliki akar-akar x1 > 1 dan x2 < 1. Maka nilai p yang memenuhi adalah …
  1. p ≠ 2
  2. p = 0
  3. p > 0
  4. 0 > p > 0
  5. p < 0

PEMBAHASAN :
x2 + px + (p – 1) = 0
a = 1 , b = – p, c = (p – 1)
x1 + x2 = – p
x1 . x2 = (p -1)
x1 > 1 → (x1 – 1) > 0
x2 < 1 → (x2 – 1) < 0
(x1 – 1)(x2 – 1) < 0
x1 . x2 – (x1 + x2 ) + 1 < 0
(p – 1) + p + 1 < 0
2p < 0
p < 0

D > 0
b2 – 4.a.c > 0
(-p)2 – 4(1)(p – 1) > 0
p2 – 4p + 4 > 0
(p – 2)2 > 0
p ≠ 2
Maka nilai p yang memenuhi dengan x1 > 1 dan x2 < 1 adalah p < 0
Jawaban : E

Soal No.38
Persamaan kuadrat mempunyai akar-akar -3 dan 4 adalah …
  1. x2 + 2x – 12 = 0
  2. x2 – 3x – 4 = 0
  3. x2 – x – 12 = 0
  4. x2 + x + 12 = 0
  5. x2 – 2x – 10 = 0

PEMBAHASAN :
Misalkan:
a1 = -3 dan a2 = 4
(a1 + a2) = 1
(a1 . a2 ) = – 12

Maka persamaan kuadrat yang terbentuk sebagai berikut:
x2 – (a1 + a2 )x + (a1 . a2 ) = 0
x2 – x – 12 = 0
Jawaban : C

Soal No.39
Jika akar-akar persamaan kuadrat 2x2 + 2x – 3 = 0 adalah p dan q. Persamaan kuadrat baru yang akar-akarnya adalah …
  1. 3x2 + 8x + 3 = 0
  2. x2 + 4x + 3 = 0
  3. 2x2 – x + 5 = 0
  4. 3x2 + x + 1 = 0
  5. x2 – 8x – 2 = 0

PEMBAHASAN :

Jawaban : A

Soal No.40
Diketahui x1 dan x2 adalah akar persamaan kuadrat dari x2 – 3x + p = 0. Maka persamaan kuadrat yang akarnya y1 = x12 + x22 dan y2 = x1 + x2 adalah …
  1. x2 – (10 + 2p)x – (20 – 6p) = 0
  2. x2 + (12 – 2p)x – (2 – 3p) = 0
  3. x2 – (12 – 2p)x + (27 – 6p) = 0
  4. x2 – (12 + 3p)x + (2 + p) = 0
  5. x2 + (1 – 3p)x + (27 – 6p) = 0

PEMBAHASAN :
x2 – 3x + p = 0
a = 1, b = -3, c = p

y1 = x12 + x22
= (x1 + x2)2 – 2(x1 . x2)
= (3)2 – 2(p)
= 9 – 2p
y2 = x1 + x2
= 3

Maka persamaan kuadrat dengan akar y1 dan y2, sebagai berikut:
x2 – (y1 + y2)x + (y1 . y2) = 0
x2 – (9 – 2p + 3)x + (9 – 2p)(3) = 0
x2 – (12 – 2p)x + (27 – 6p) = 0
Jawaban : C

Soal No.41
Akar-akar persamaan kuadrat 2x2 – 6x + 4 = 0 adalah m dan n. Persamaan kuadrat baru yang akar-akarnya (m + 1) dan (n + 1) adalah …
  1. x2 – 5x + 6 = 0
  2. x2 + 3x + 2 = 0
  3. x2 – 5x – 3 = 0
  4. 2x2 + x + 6 = 0
  5. 3x2 – 8x + 6 = 0

PEMBAHASAN :
2x2 – 6x + 4 = 0
a = 2, b = – 6, c = 4
(m + n) = 3
(m . n) = 2
Misalkan:
y1 = m + 1
y2 = n + 1
y1 + y2 = (m + 1) + (n + 1)
= (m + n) + 2
= 3 + 2
= 5
y1 . y2 = (m + 1) . (n + 1)
= (m.n) + (m + n) + 1
= 2 + 3 + 1
= 6

Maka persamaan kuadrat baru yang akar-akarnya y1 dan y2 sebagai berikut:
x2 – (y1 + y2)x + (y1 . y2) = 0
x2 – 5x + 6 = 0
Jawaban : A

Soal No.42
Diketahui x1 dan x2 merupakan akar-akar persamaan x2 – x + 3 = 0. Maka persamaan kuadrat baru yang akar-akarnya 3x1 – 3 dan 3x2 – 3 adalah …
  1. x2 – 2x + 15 = 0
  2. x2 – 3x – 10 = 0
  3. x2 + 3x + 15 = 0
  4. x2 + 2x + 12 = 0
  5. x2 + 5x + 20 = 0

PEMBAHASAN :
x2 – x + 3 = 0
a = 1 , b = -1 , c = 3
x1 + x2 = 1
x1 . x2 = 3
Misalkan akar-akar dari persamaan kuadrat yang baru adalah p dan q, yaitu:
p + q = (3x1 – 3) + (3x2 – 3)
= 3(x1 + x2) – 6
= 3(1) – 6
= – 3
p . q = (3x1 – 3)(3x2 – 3)
= 3( x1 . x2) – 3(x1 + x2) + 9
= 3(3) – 3(1) + 9
= 9 – 3 + 9
= 15

Maka persamaan kuadrat yang baru sebagai berikut:
x2 – (p + q)x + (p.q) = 0
x2 – (- 3)x + 15 = 0
x2 + 3x + 15 = 0
Jawaban : C

Soal No.43
Persamaan kuadrat yang masing-masing akarnya 2 kali akar persamaan kuadrat x2 + mx + n = 0 adalah …
  1. 2x2 + 2mx + 2n = 0
  2. x2 + 2mx + 4n = 0
  3. x2 – mx + 2n = 0
  4. 3x2 – 2mx – 4n = 0
  5. x2 + 4mx – 4n = 0

PEMBAHASAN :
Berlaku invers akar sebagai berikut:
Maka persamaan kuadrat baru adalah

Kalikan 4, menjadi:
x2 + 2mx + 4n = 0
Jawaban : B

Soal No.44
Jika m dan n akar-akar persamaan kuadrat 2x2 + 4x + 6 = 0. Maka persamaan kuadrat yang memiliki akar-akar (2m + n + 1) dan (m + 2n + 1) adalah …
  1. x2 – 2x + 3 = 0
  2. x2 + x + 6 = 0
  3. x2 – 4x – 2 = 0
  4. x2 + x + 1 = 0
  5. x2 + 4x + 6 = 0

PEMBAHASAN :
2x2 + 4x + 6 = 0
a = 2 , b = 4 , c = 6
Misalkan:
y1 = 2m + n + 1
y2 = m + 2n + 1
m + n = – 2
m . n = 3
y1 = 2m + n + 1
= (m + n) + m + 1
= – 2 + m + 1
= m – 1
y2 = m + 2n + 1
= (m + n) + n + 1
= – 2 + n + 1
= n – 1
y1 + y2 = (m – 1) + (n – 1) = (m + n) – 2 = – 2 – 2 = – 4
y1 . y2 = (m – 1) . (n – 1) = mn – (m + n) + 1 = 3 – (- 2) + 1 = 6
Maka persamaan kuadrat dengan akar-akar y1 dan y2 sebagai berikut:
x2 – (y1 + y2)x + (y1 . y2) = 0
x2 – (- 4)x + 6 = 0
x2 + 4x + 6 = 0
Jawaban : E

Soal No.45
Terdapat akar-akar dari 2x2 + 8x – p = 0, merupakan x1 dan x2. Jika x1 – x2 = 6, maka nilai p adalah …
  1. 12
  2. 20
  3. 10
  4. 14
  5. 15

PEMBAHASAN :
Untuk soal di atas berlaku rumus sebagai berikut:
contoh soal persamaan kuadrat
2x2 + 8x – p = 0
a = 2
b = 8
c = -p
contoh soal persamaan kuadrat
Jawaban : C

Soal No.46
Diketahui persamaan kuadrat x2 – px + p +1 = 0, memiliki akar-akar x1 dan x2 . Jika x1 – x2 = 1, maka nilai p adalah …
  1. 5 atau – 1
  2. – 3 atau – 1
  3. 5 atau – 2
  4. – 5 atau – 1
  5. 5 atau 1

PEMBAHASAN :
Untuk soal di atas berlaku rumus sebagai berikut:
contoh soal persamaan kuadrat
x2 – px + p +1 = 0
a = 1
b = -p
c = p + 1
x1 – x2 = 1

P2 – 4p – 4 = 1
P2 – 4p – 5 = 0
(p – 5)(p + 1) = 0
p = 5 atau p = -1
Jawaban : A

Soal No.47
Terdapat akar-akar persamaan kuadrat x2  + 3x + 4 = 0 yaitu α dan β. Persamaan kuadrat baru dengan akar-akarnya (α – 2) dan (β – 2) adalah …
  1. x2 – 7x – 4 = 0
  2. x2 – 3x – 2 = 0
  3. x2 + 5x – 2 = 0
  4. x2 + 7x – 2 = 0
  5. x2 + 7x + 4 = 0

PEMBAHASAN :
x2  + 3x + 4 = 0 dengan akar-akar α dan β, maka:
a = 1
b = 3
c = 4
contoh soal persamaan kuadrat

Maka persamaan kuadrat baru dengan akar-akar (α – 2) dan (β -2) sebagai berikut:
x2 – ((α – 2) + (β – 2))x + (α – 2)(β – 2) = 0
x2 – (α + β – 4)x + (αβ – 2α – 2β + 4) = 0
x2 – (- 3 – 4)x + (4 – 2(α + β) + 4 = 0
x2 + 7x + 2(-3) + 4 = 0
x2 + 7x – 2 = 0
Jawaban : D

Soal No.48
Diketahui persamaan kuadrat (p – 1)x2 + 4x + 2p = 0, memiliki akar-akar real dan berbeda. Maka nilai p adalah …
  1. 1 < p < 2
  2. 1 < p < – 2
  3. – 1 < p < 2
  4. – 2 < p < -1
  5. – 1 < p < – 2

PEMBAHASAN :
(p – 1)x2 + 4x + 2p = 0
a = p – 1
b = 4
c = 2p

Persamaan kuadrat dengan akar-akar real berbeda adalah D > 0, berlaku:
b2 – 4.a.c > 0
42 – 4(p – 1).2p > 0
16 – 8p(p – 1) > 0
16 – 8p2 + 8p > 0
Kalikan negatif
8p2 – 8p – 16 < 0
p2 – p – 2 < 0
(p – 2)(p + 1) < 0
p1 = 2 atau p2 = -1
contoh soal persamaan kuadrat
Maka nilai p: – 1 < p < 2
Jawaban : C

Soal No.49
Diketahui m dan n merupakan akar-akar persamaan kuadrat x2 – 5x – 6 = 0. Maka persamaan kuadrat baru yang akar-akarnya contoh soal persamaan kuadrat dan contoh soal persamaan kuadrat adalah …
  1. 6x2 + 5x + 1 = 0
  2. 6x2 – 5x – 1 = 0
  3. – 6x2 + 5x – 1 = 0
  4. – 6x2 – 5x + 1 = 0
  5. 6x2 – 5x + 1 = 0

PEMBAHASAN :
x2 – 5x – 6 = 0
a = 1
b = – 5
c = – 6
contoh soal persamaan kuadrat

Maka persamaan kuadrat baru dengan akar-akar  dan  sebagai berikut:
contoh soal persamaan kuadrat
Kalikan dengan enam, menjadi:
6x2 – 5x – 1 = 0
Jawaban : B

Soal No.49
Diketahui m dan n merupakan akar-akar persamaan kuadrat x2 – 5x – 6 = 0. Maka persamaan kuadrat baru yang akar-akarnya contoh soal persamaan kuadrat dan contoh soal persamaan kuadrat adalah …
  1. 6x2 + 5x + 1 = 0
  2. 6x2 – 5x – 1 = 0
  3. – 6x2 + 5x – 1 = 0
  4. – 6x2 – 5x + 1 = 0
  5. 6x2 – 5x + 1 = 0

PEMBAHASAN :
x2 – 5x – 6 = 0
a = 1
b = – 5
c = – 6
contoh soal persamaan kuadrat

Maka persamaan kuadrat baru dengan akar-akar  dan  sebagai berikut:
contoh soal persamaan kuadrat
Kalikan dengan enam, menjadi:
6x2 – 5x – 1 = 0
Jawaban : B

Soal No.50
Jika persamaan kuadrat 2x2 – 5x + 3 = 0 akar-akarnya x1 dan x2 . Maka nilai dari contoh soal persamaan kuadrat
  1. contoh soal persamaan kuadrat
  2. contoh soal persamaan kuadrat
  3. contoh soal persamaan kuadrat
  4. contoh soal persamaan kuadrat
  5. contoh soal persamaan kuadrat

PEMBAHASAN :
2x2 – 5x + 3 = 0 akar-akarnya x1 dan x2
a = 2
b = – 5
c = 3
contoh soal persamaan kuadrat
maka
contoh soal persamaan kuadrat
Jawaban : A

Fitur Terbaru!!

Kini kamu bisa bertanya soal yang tidak ada di artikel kami.
Ajukan pernyataan dan dapatkan jawaban dari tim ahli kami.
Untuk bertanya KLIK DISINI

TagContoh Soal Matematika SMA Matematika Kelas X Pembahasan Soal Matematika SMA Persamaan Kuadrat Rangkuman Materi Matematika

Sebelumnya Rangkuman, 45 Contoh Soal Matriks Jawaban +Pembahasan
Selanjutnya Rangkuman, 53 Contoh Soal Integral Pembahasan & Jawaban

9 Komentar

  1. Naufal
    27/06/2018 at 5:18 am

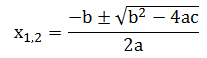
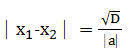
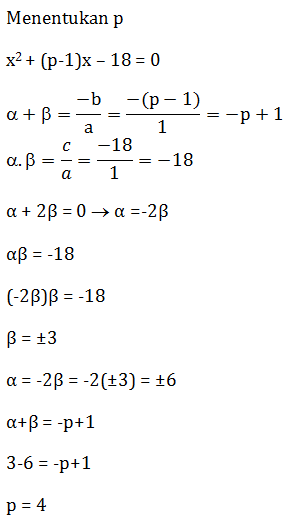
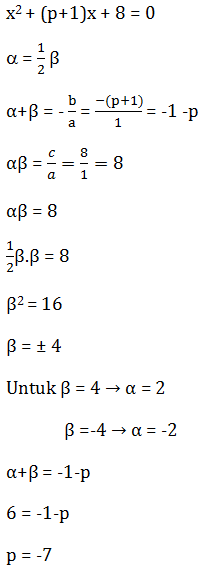
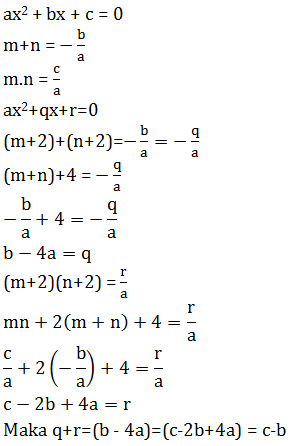
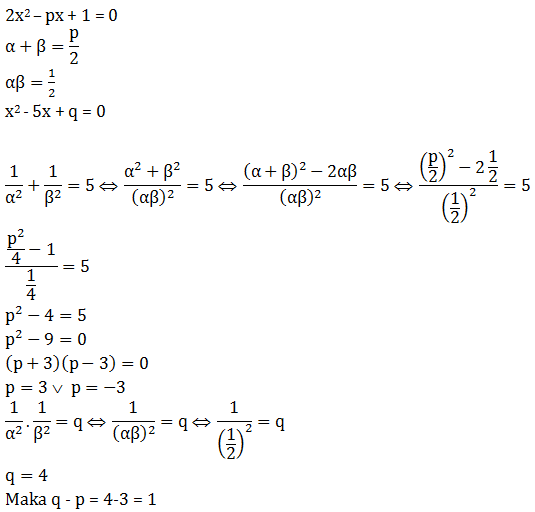
    Mantab nih soalnya tapi masih kurang banyak dan klo bisa bikin youtube soal dan pembahasan tentang persamaan kuadrat. Tolong diperbarui ya, soalnya ini artikel sangat bermanfaat buat saya apalagi ada vidionya tambah tip deh.

    Reply
  2. Stella
    15/07/2018 at 12:20 pm

    Itu untuk soal no.4.. 4a dari mana yah ?

    Reply
  3. Pitra
    05/04/2019 at 8:21 pm

    Ini Pelajaran Untuk SMK kelas XI Kak ?

    Reply
  4. Freya
    01/06/2019 at 7:16 pm

    Soal no 8 di pembahasan ada 2a+4 =0 dapet dari mana ya?

    Reply
  5. Vita
    06/10/2020 at 1:05 pm

    keren banget situsnya menyediakan materi sma dengan lengkap beserta contoh soal dan pembahasannya, ini sangat membantu sekali

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.

Kebijakan Privasi | Syarat & Ketentuan
© Copyright 2023, tanya-tanya.com. All Rights Reserved