Rangkuman Materi Kinematika Gerak Kelas 10

Gerak Lurus

1. Perpindahan (∆s)

   Yaitu perubahan posisi awal so ke posisi akhir s, berlaku:
   ∆s = s-so
2. Kecepatan dan Kelajuan Rata-RataDua jenis kecepatan yaitu:
   Kecepatan Rata-rata (v)
   
   Kelajuan Rata-rata (v)
   Kecepatan Sesaat(v)
   
3. Percepatan

   Yaitu perubahan kecepatan benda dalam selang waktu tertentu.
   Percepatan Rata-Rata
   
   Percepatan Sesaat
   

4. Gerak Lurus Beraturan (GLB)

   Yaitu Gerak benda pada lintasan lurus dengan kecepatan konstan dengan percepatan = 0. Rumusannya sebagai berikut:
   
   Keterangan:
   v=kecepatan (m/s)
   s=jarak (m)
   t=waktu(s)

5. Gerak Lurus Berubah Beraturan (GLBB)

   Yaitu gerak benda pada lintasan lurus dengan kecepatan berubah secara beraturan dengan percepatan benda konstan.
   Persamaan GLBB yaitu sebagai berikut:
   s=v_o.t + 1/2 a.t²
   v_t = v_o + a.t
   v_t² = v_o² + 2as
   keterangan:
   v_t = kecepatan akhir (m/s)
   v_o = kecepatan awal (m/s)
   a = percepatan (m/s2)
   s = jarak (m)
   t = waktu (s)
   jika dalam bentuk grafik kecepatan v terhadap waktu t
   
   jadi
   s = luas kurva pada selang waktu tertentu

6. Gerak Jatuh Bebas

   yaitu gerak jatuh benda tanpa kecepatan awal atau Vo=0
   Kecepatan benda saat mencapai permukaan tanah (v_t)
   
   Waktu hingga mencapai tanah (t)
   
   Keterangan:
   h= ketinggian benda (m)
   g= percepatan gravitasi bumi (m/s²)

7. Gerak Vertikal

Gerak Parabola

Yaitu perpaduan antara gerak lurus beraturan yang arahya searah sumbu x dan gerak vertikal yang arahnya searah sumbu y.

1. Ketinggian Maksimum (hmaks)

   Pada ketinggian maksimum berlaku v=0 sehingga:
   

2. Waktu yang diperlukan ketika hmaks

   

3. Jarak Maksimum (xmaks)

   Jarak benda terjauh, berlaku:
   

4. Waktu yang diperlukan untuk x_maks

   

   Gerak Melingkar

   1. Perpindahan Sudut (Δθ)

      yaitu sudut yang dilewati oleh sebuah garis radial mulai dari posisi awal (θ_o) sampai posisi akhir (θ), Rumusannya:
      Δθ = θ – θ_o

   2. Kecepatan sudut rata-rata dan sesaat

      Kecepatan sudut rata-rata (w)
      
      Kecepetan sudut sesaat (w)
      

   3. Percepatan sudut

yaitu perubahan kecepatan sudut benda dalam selang waktu tertentu dalam gerak melingkar
Percepatan Sudut Rata-Rata

Percepatan Sudut Sesaat

Hubungan percepatan sudut (a) dan percepatan linier (a)

keterangan :
r = jari-jari lingkaran (m)

Gerak Melingkar Beraturan

yaitu gerak benda pada lintasan berupa lingkaran dengan kecepatan sudut tetap.

1. Frekuensi dan Periode

   Frekuensi (f) yaitu banyaknya putaran per detik rumusnya :
   
   Periode (T) adalah waktu yang di perlakukan untuk berotasi satu putaran, rumusnya :
   
   Maka
   Keterangan:
   ƒ = Frekuensi (Hz)
   n = jumlah putaran
   t = waktu (s)
   T = periode (s)

2. Kecepatan Sudut

   Yaitu besarnya sudut yang ditempuh tiap satuan waktu. Rumusannya sebagai berikut.
   
   v = ω R
   Keterangan
   ω = kecepatan sudut (rad/s)
   v = kecepatan linier (m/s)
   R = jari – jari lintasan (m)

3. Percepatan Sentripetal

   Yaitu percepatan benda yang bergerak melingkar yang memiliki arah menuju ke pusat.
   Rumusnya sebagai berikut.
   
   Keterangan :
   a_s = percepatan sentripetal (m/s²)

4. Percepatan Total

   yatu resultan dari percepatan linier/percepatan tangensial (a_t) dengan percepatan sentripetal (a_s) sehingga memenuhi persamaan:
   

5. Hubungan roda-roda dalam gerak melingkar beraturan

   Satu tali bersinggungan
   
   v_A = v_B Maka ω_A R_A = ω_B R_B

   Satu sumbu putar
   
   ω_A = ω_B Maka
   Keterangan:
   v = kecepatan linier (m/s)
   ω = kecepatan sudut (ras/s)
   R = jari-jari roda (m)

Contoh Soal Kinematika Gerak Pembahasan & Jawaban Kelas 10

Soal No.2 (SBMPTN 2018)

Posisi suatu benda sepanjang sumbu x mengikuti persamaan x(t) = -6t + 2t², dengan satuan untuk posisi (x) adalah meter dan untuk waktu (t) adalah detik. Pada selang waktu dari t = 1 detik sampai t = 3 detik, perpindahan dan percepatan rata-rata benda tersebut berturut-turut adalah….

1. 4 m dan 0 m/s²
2. 4 m dan 4 m/s²
3. 4 m dan 4m/s
4. 2 m dan 1 m/s
5. 4 m dan 2 m/s²

PEMBAHASAN :
Perpindahan adalah perubahan posisi dalam selang waktu tertentu. Perpindahan hanya tergantung pada posisi akhir dan posisi awal, tidak tergantung lintasan yang ditempuh.
Untuk posisi pada saat t = 1 detik
x(1) = -6(1)+2(1)²
x(1) = -4 meter
x(3) = -6(3)+2(3)²
x(3) = 0 meter
Δx = x(3) –  x(1)
Δx = 0 – (-4)
Δx = 4 meter
Percepatan rata-rata adalah hasil bagi antara perubahan kecepatan dengan selang waktu.

Dengan
a= percepatan rata-rata
Δv = perubahan kecepatan
Δt = selang waktu
Untuk mencari kelajuan pada waktu tertentu tertentu dari persamaan posisi terhadap waktu diperoleh persamaan berikut ini.

v = -6+4t
v(3) = −6+4(3)
v(3) =6
v(1) = −6+4(1)
v(1) = -2 m/s
Dengan demikian percepatan rata – rata dari t = 1 detik s.d t = 3 detik adalah:

Jawaban B

Soal No.3 (SBMPTN 2018)

Sebuah benda bermasssa m diikat oleh seutas tali dengan panjang L = 2,5 m dan berada pada suatu permukaan luar kerucut yang licin seperti pada gambar. Rotasi benda berlawanan dengan arah gerak jarum jam terhadap sumbu putar O dengan laju putar yang konstan. Jika tan θ = 0,75, nilai laju putar ω agar gaya normal antara benda dan permukaan kerucut bernilai nol adalah….

1. 
2. 
3. 
4. 
5. 

PEMBAHASAN :
Diketahui:
L = 2,5 m
Tan θ = ¾ akibatnya  cos θ = 4/5

Ditanya:
ω (Kecepatan sudut)

Solusi
Menggambarkan gaya – gaya yang terlibat pada benda.

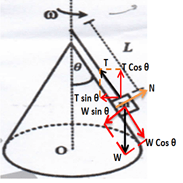
Dari gambar, searah sumbu y benda diam artinya ΣF_y = 0 dengan demikian
ΣF_atas = ΣF_bawah
T cos θ = w
T cos θ = mg
             (1)
Pada arah sumbu X benda berputar dengan nilai N = 0 (dari soal) sehingga faktor N diabaikan. Pada saat benda bergerak melingkar beraturan dengan jari – jari R timbul percepatan sentripetal. Jika ada percepatan sentripetal maka timbul gaya, gaya ini disebut gaya sentripetal, F_SP
ΣF_sp = m ω² R     (2)
Secara teknis, gaya –gaya yang mempengaruhi benda pada saat benda bergerak melingkar dapat berperan sebagai gaya sentripetal.
ΣF_sp = ΣF_{menuju pusat lingkaran} – ΣF_{menjauhi pusat lingkaran}
Pada gambar:
ΣF_sp = ΣF_{menuju pusat lingkaran} – ΣF_{menjauhi pusat lingkaran}
ΣF_{menjauhi pusat lingkaran} = 0 karena pada arah ini tidak ada gaya
ΣF_sp = T sin θ                     (3)

Subsitusi 1 dan 2 ke persamaan 3, diperoleh
                        (4)
Untuk mencari R, Perhatikan gambar berikut.

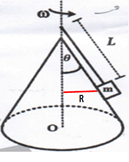
Dari gambar hubungan θ, L dan R adalah

R = L sin θ           (5)

Subsitusi 4 ke 5 maka diperoleh:



ω² (2,5) = 12,5
ω² (2,5) = 5
ω² = 5
ω =  rad/s
Jawaban C

Grafik di samping menyatakan hubungan antara jarak (s) terhadap (t) dari benda yang bergerak , Bila s dalam m , dan t dalam sekon maka kecepatan rata-rata benda adalah…..

1. 0,60 m/s
2. 1,67 m/s
3. 2,50 m/s
4. 3,0 m/s
5. 4,6 m/s

PEMBAHASAN :
Untuk menentukan kecepatan rata-rata (v) kita akan menggunakan rumus:


V = = 1,67 m/s
Jawaban : A

1. 5 sekon
2. 10 sekon
3. 17 sekon
4. 25 sekon
5. 35 sekon

PEMBAHASAN :
Diketahui v_o = 36 km/jam = 10 m/s
v_t = 72 km/jam = 20 m/s
Jarak s = 150 m

Masukan ke persamaan
v_t² = v_o² + 2as


t = 10 s
Jawaban B

PEMBAHASAN :
Karena benda x merupakan gerak jatuh bebas dengan ketinggian h₀ = D, maka:
h_x = h₀ – 1/2 gt²
h_x = D – gt²
benda y bergerak vertikal ke atas
h_y = v₀ – 1/2 gt²
h_y = vt – 1/2 gt²
berlaku h_x = h_y
D – gt² = vt – 1/2 gt²
D = vt

Jawaban E

1. 5 m/s
2. 10 m/s
3. 15 m/s
4. 20 m/s
5. 25 m/s

PEMBAHASAN :
Kita akan menghitung waktu benda 1 ketika mencapai tanah menggunakan rumusan gerak jatuh bebas

karena di soal diketahui Benda Kedua (Benda 2) dijatuhkan 1 detik kemudian, maka:
t₂= t₁ –1 = 2 – 1 s= 1 s
masukan ke persamaan
h₁ = h_o –v₀t – 1/2 gt²
0 = 20 – v₀ – 5
v₀ = 15 m/s
Jawaban C

Sebuah batu dilempar dari atas tebing setinggi 30 m dengan kecepatan 20 m/s berarah 30^o terhadap horizontal seperti pada gambar.

1. 1 : 2 √3
2. 2 √3 : 1
3. 3 : 2 √3
4. 2 √3 : 3
5. 1 : 2

PEMBAHASAN :
Menentukan kecepatan pada sumbu x
v_x = v₀ cos α
v_x = 20 cos 30^o = m/s
Menentukan panjang x
x = v t = . 3 = m
menentukan kecepatan di sumbu y
v_y = v_o sin α
v_y = 20 sin 30^o = 10 m/s
menentukan tinggi h
h = h₀ + v₀t – 1/2 gt²
h = 30 + 20.3 – 10.3²
h = 45 m
perbandingan
h : x = 45 :
h : x = 3 : 2√3
Jawaban C

Sebuah benda bergerak melingkar dengan kecepatan sudut bertambah besar. Pada waktu t ,sudut 0 yang di tempuh oleh benda dengan kecepatan sudut w adalah sebagai berikut

[table caption=”” width=”300″ colwidth=”20|20|20″ colalign=”center|center|center”] t(s),θ (rad),ω (rad s^-1)
2,14,11
4,44,19
6,90,27
8,152,35
[/table]

1. 4,5 rad s² saat t = 6 s dan berkurang secara bertahap
2. Konstan 4 rad s^-2
3. Konstan 8 rad s^-2
4. 15 rad s² saat t = 8 s dan bertambah dengan pertambahan tetap
5. 4,5 rad s² saat t = 6 s dan betambah secara bertahap

PEMBAHASAN :
Menghitung percepatan sudut beda untuk tiga selang waktu
selang waktu I (2 s.d 4 sekon)

selang waktu II (4 s.d 6 sekon)

selang waktu III (6 s.d 8 sekon)

Semuanya konstan 4 rad s^-2
Jawaban B

1. 1,2
2. 2,1
3. 3,6
4. 3,9
5. 5,1

PEMBAHASAN :
Menghitung Percepatan total mengggunakan rumus:

menghitung a tangensial
a_t = α.R = 15.0,1 = 1,5 m/s²
menghitung dari rumus:
ωt = ωo + at = 0 + 15.0,4 = 6 rad/s
menghitung v dengan rumus
v = ω R = 6.0,1 = 0,6 m/s

masukan ke rumus a_total

Jawaban D

1. 50 m/s dan 2500 m/s²
2. 
3. 
4. 
5. 

PEMBAHASAN :
Diketahui diameter baskom d = 1 m
R = 0,5 m

Menghitung v
v = ωR


Menghitung percepatan sentripetal



Jawaban D

Dua roda A dan B dihubungkan dengan pita (lihat gambar). Apabila jari=jari A dua kali jari-jari B maka yang terjadi adalah…

1. v_A = 2v_B
2. v_A = v_B
3. v_A = v_B
4. v_A = v_B
5. v_A = 2 v_B

PEMBAHASAN :
Gambar tersebut

memiliki v_A = v_B
Jawaban C

1. 1 s
2. 2 s
3. 
4. 
5. 

PEMBAHASAN :
Diketahui
Vo = 20 m/s
ά = 60o
g = 10 m/s
Menghitung waktu ketika ketinggian maksimum



Jawaban C

1. t_A – t_B
2. t_B – t_C
3. t_A – t_C
4. t_C – t_D
5. t_D – t_E

PEMBAHASAN :
Jika diketahui kurva x terhadap t, benda yang bergerak lurus beraturan berupa garis lurus dengan gradien yang linear. Maka selang waktunya adalah t_C – t_D
Jawaban D

1. 10 km
2. 20 km
3. 30 km
4. 40 km
5. 50 km

PEMBAHASAN :
Diketahui:
v = 40 km/jam
t = 15 menit = 0,25 jam

Maka jarak yang ditempuh dapat dihitung sebagai berikut:
S = v . t
= 40 . 0,25
= 10 km
Jawaban A

1. 14 m
2. 22 m
3. 32 m
4. 40 m
5. 54 m

PEMBAHASAN :
Diketahui:
v₁ = 8 m/s
v₀ = 0
t = 2 sekon

Menentukan percepatan sebagai berikut:

Maka jarak yang ditempuh selama 4 sekon dapat dihitung sebagai berikut:
S = v₀ . t + ½ . a . t²
= 0 + ½ . 4 . 4²
= ½ . 4 . 16
= 32 m
Jawaban C

1. 180,5 m
2. 168,8 m
3. 283,8 m
4. 113,4 m
5. 183,8 m

PEMBAHASAN :
Diketahui:
v₀ = 60 m/s
g = 9,8 m/s²

Menentukan v₁ sebagai berikut:
v₁ = v₀ – g.t
0 = 60 – 9,8t

Maka ketinggian maksimum dapat dihitung sebagai berikut:
y = v₀ . t – ½ g.t²
= 60(6,12) – ½ (9,8)(6,12)²
= 367,3 – 183,5
= 183,8 m
Jawaban E

1. 3,2 s
2. 2 s
3. 0,5 s
4. 4,1 s
5. 5 s

PEMBAHASAN :
Diketahui:
h = 50 m
g = 10 m/s²

Maka waktu ketika benda mencapai tanah dapat dihitung sebagai berikut:
h = ½ . g.t

Jawaban A

1. 100 rad/s
2. 78 rad/s
3. 90 rad/s
4. 83 rad/s
5. 69 rad/s

PEMBAHASAN :
Diketahui:
r = 30 cm = 0,3 m
v = 90 km/jam = 25 m/s

Maka kecepatan sudut roda dapat dihitung sebagai berikut:
v = ω. r

Jawaban D