Rangkuman Materi Garis & Sudut Kelas 7 SMP

Garis

• Garis merupakan kumpulan titik-titik yang berderet (ke kanan atau kiri atau atas atau bawah) serta jaraknya saling berdekatan satu sama lain. Garis tidak memiliki ujung dan tidak memiliki pangkal.
  
  Menurut bentuknya garis dibedakan menjadi 2 macam, yaitu:
  • Garis vertikal: garis tegak lurus
    
  • Garis horizontal: garis mendatar (sejajar horizon)
    
• Ruas garis adalah kurva lurus yang berpangkal dan berujung karena terdapat titik pada pangkal dan ujungnya.
  
• Sinar garis yaitu sebuah garis yang diawali dengan satu titik kemudian berlanjut berderet ke satu arah (ujung lainnya) membentang tak terbatas.
  

Kedudukan Dua Garis

Macam-macam kedudukan dua garis:

1. Dua garis sejajar, yaitu dua garis sejajar yang berada dalam satu bidang datar yang tidak akan pernah bertemu atau berpotongan walaupun kedua garis tersebut diperpanjang hingga tak berhingga. Garis sejajar dilambangkan dengan “ // “. Garis sejajar memiliki sifat-sifat sebagai berikut:
2. Melalui sebuah titik di luar garis dapat ditarik sebuah garis lurus lain yang sejajar.
3. ketika sebuah garis memotong salah satu dari dua garis yang sejajar maka garis tersebut akan memotong garis yang lain.
4. Apabila sebuah garis sejajar dengan dua garis lainnya maka kedua garis itu akan saling sejajar satu sama lain.
   
5. Dua garis berpotongan, yaitu dua buah garis yang terletak pada bidang datar dan berpotongan di satu titik potong (titik persekutuan).
   
6. Dua garis berimpit, yaitu dua garis terletak pada satu garis lurus sehingga setidaknya memiliki dua titik potong.
   
7. Dua garis bersilangan, yaitu dua garis yang tidak sejajar, tidak terletak pada satu bidang datar, dan tidak akan berpotongan jika diperpanjang.
   

Sudut

Sudut merupakan suatu daerah yang terbentuk dari sebuah sinar yang diputar pada pangkal sinarnya  atau pertemuan dua ruas garis yang bertemu pada satu titik. Sudut dilambangkan dengan symbol “Д dan  satuannya adalah derajat (⁰ ).

Macam – Macam Sudut

Berdasarkan besar sudutnya, sudut dibedakan menjadi:

1. Sudut lancip: sudut yang besar sudutnya antara 0⁰ – 90⁰ .
   
2. Sudut tumpul: sudut yang besar sudutnya antara 90⁰ – 180⁰.
   
3. Sudut siku-siku: sudut yang besar sudutnya 90⁰.
   
4. Sudut lurus: sudut yang besar sudutnya 180⁰.
   
5. Sudut reflex: sudut yang besar sudutnya lebih dari 180⁰ tapi kurang dari 360⁰.
   

Hubungan Antarsudut

1. Sudut saling berpelurus (bersuplemen): besar jumlah dua sudut yang saling berpelurus (bersuplemen) adalah 180⁰Contoh:
   
   ∠POR  + ∠QOR  = 180⁰
   Contoh:
   ∠P = 60⁰ , maka suplemennya = 180⁰ –  60⁰  = 120⁰
2. Sudut saling berpenyiku (berkomplemen): besar jumlah dua sudut yang berpenyiku adalah 90⁰
   
   ∠POQ + ∠QOR = 90⁰
   Contoh:
   ∠P = 35⁰ , maka komplemennya = 90⁰ – 35⁰ = 65⁰
   1. Sudut saling bertolak belakang: dua sudut yang saling bertolak belakang memiliki besar sudut yang sama. Sudut tersebut letaknya saling membelakangi.
      Contoh:
      
      ∠POQ = ∠ROS = 75⁰

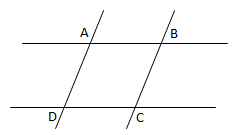
Hubungan Antarsudut Jika Dua Garis Sejajar Dipotong Oleh Sebuah Garis Lurus 

1. Sudut-sudut sehadap besar sudutnya sama besar yaitu:
   ∠A = ∠E
   ∠B = ∠F
   ∠C = ∠H
   ∠D = ∠G
2. Sudut-sudut bersebrangan
   Besar sudutnya sama besar, dibagi menjadi dua yaitu:
   • Dalam bersebrangan
     ∠C = ∠E
     ∠D = ∠F
   • Luar bersebrangan
     ∠A = ∠G
     ∠B = ∠H
3. Sudut-sudut dalam sepihak
   Sudut-sudut sepihak membentuk sudut 180⁰
   ∠D + ∠E = 180⁰
   ∠C + ∠F = 180⁰
4. Sudut-sudut luar sepihak
   Sudut-sudut luar sepihak membentuk sudut 180⁰
   ∠B + ∠G = 180⁰
   ∠A + ∠H = 180⁰

Contoh Soal & Pembahasan Garis & Sudut Kelas 7 SMP

1. 60^o
2. 90^o
3. 120^o
4. 150^o

PEMBAHASAN :
Jumlah sudut adalah 180^o
Maka:
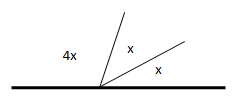
4x + x + x = 180^o
6x = 180^o
x = 30^o
Sudut yang terbesar adalah 4x sehingga sudutnya
4x = 4. 30^o = 120^o
Jawaban C

1. 40^o
2. 50^o
3. 90^o
4. 120^o

PEMBAHASAN :
Sudut yang saling berpenyiku memiliki jumlah sudut = 90^o


Maka sudut yang terbesarnya adalah 50^o
Jawaban B

1. 24^o
2. 60^o
3. 75^o
4. 82^o

PEMBAHASAN :
Jumlah sudut berpenyiku = 90^o
∠P + ∠Q = 90^o
(2x + 8) + (x – 5) = 90
2x + x + 8 – 5 = 90
3x + 3 = 90
3x = 90 – 3 = 87

maka ∠Q
∠Q = x – 5 = 29 – 5 = 24^o
Jawaban A

1. 10^o
2. 12,5^o
3. 30^o
4. 45^o
5. 60^o

PEMBAHASAN :
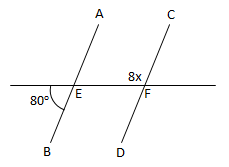
Menentukan ∠FEB
∠FEB = 180^o – 80^o = 100^o
∠CFE akan sama dengan ∠FEB karena merupakan pasangan sudut luar bersebrangan
∠CFE = 100^o = 8x
8x = 100^o
x = 12,5^o
Jawaban C

1. 50^o
2. 60^o
3. 70^o
4. 80^o

PEMBAHASAN :
Diketahi perbandingan sudut dengan pelurusnya adalah 7 : 11. Jika dijumlahkan dua sudut yang saling berpelurus jumlahnya adalah 180^o
Menentukan besarnya sudut

Jawaban C

1. 120^o
2. 130^o
3. 150^o
4. 160^o

PEMBAHASAN :
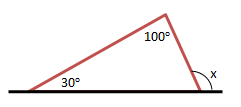
Jumlah sudut dalam segitiga = 180^o
Sudut segitiga di dekat x adalah
180 – (100 + 30) = 50^o
Maka sudut x adalah
x + 50^o = 180^o
x = 180^o – 50^o = 130^o
Jawaban B

1. 30^o
2. 40^o
3. 50^o
4. 60^o

PEMBAHASAN :
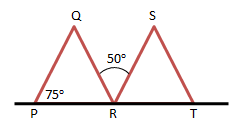
∠QPR sehadap dengan ∠SRT maka
∠SRT sama dengan ∠QPR yaitu 75^o
Jumlah sudut dalam segitiga adalah 180^o
maka ∠PRQ = 180 – (75 + 55) = 180 – 130 = 50^o
Jawaban C

PEMBAHASAN :
Jumlah sudutnya adalah 180^o
Maka:
4x + 90 + 3x + 6 = 180
7x + 96 = 180
7x = 180 – 96 = 84
7x = 84
x = 12
Jawaban A

PEMBAHASAN 
Menentukan panjang QR melalui perbandingan

Maka panjang PR
PR = PQ + QR = 42 + 26 = 68 cm
Jawaban B

1. 60^o
2. 70^o
3. 80^o
4. 85^o

PEMBAHASAN :
∠BAD dijumlahkan ∠ADC akan menghasilkan sudut 180^o
∠BAD + ∠ADC = 180^o
Jika ∠ADC = a, maka ∠BAD
∠BAD – ∠ADC = 40^o
∠BAD – a = 40^o
∠BAD = 45^o + a
Sehingga
∠BAD + ∠ADC = 180
(40 + a) + a = 180
40 + 2a = 180
2a = 180 – 40 = 140
2a = 140
a = 70^o = ∠ADC
Jawaban B