Contoh Soal & Pembahasan Persamaan Garis Lurus Kelas 8 SMP

1. 5
2. 6
3. 7
4. 8

PEMBAHASAN :
Diketahui persamaan garis 3y – x + 4 = 0 dengan y = 3
Substitusikan nilai y ke persamaan
3. 3 – x + 4 = 0
9 – x + 4 = 0
-x = 4 – 9 = -5 ….dikalikan -1
x = 5
Jawaban A

1. -1
2. -½
3. 1
4. 2

PEMBAHASAN :
Persamaan 2y + x = 6 diubah bentuknya menjadi y = mx + c
Menjadi
2y = -x + 6…..dibagi 2
y = -½x + 3
maka gradiennya adalah -½
Jawaban B

1. (-2, 0)
2. (-1, 0)
3. (1, 0)
4. (2, 0)

PEMBAHASAN :
Agar memiliki titik potong terhadap sumbu x maka syaratnya y = 0
5y + 6x – 12 = 0
5.0 + 6x – 12 = 0
6x – 12 = 0
6x = 12
x = 2
Maka koordinat titik potong terhadap sumbu x adalah (2, 0)
Jawaban D

1. 1. ½
   2. 1
   3. 3
   4. 5

PEMBAHASAN :
Menentukan gradien garis yang melalui titik (x₁, y₁) dan (x₂, y₂) adalah:

Jawaban B

1. -2
2. -1
3. -½
4. 1

PEMBAHASAN :
Garis a dan b sejajar, maka:
gradien garis a = gradien garis b
Menentukan gradien garis a
4y + 2x – 7 = 0
diubah ke bentuk y = mx + c
4y = -2x + 7
y = -½x +
maka gradien garis a = gradien garis b = -½
Jawaban C

1. 2y + 3x +8 = 0
2. y – 3x + 2 = 0
3. y + 3x -2 = 0
4. 2y – 3x – 8 = 0

PEMBAHASAN :
Menentukan persamaan garis yang memiliki m = 3 melewati titik (2, 4)
y – y₁ = m(x – x₁)
y – 4 = 3(x – 2)
y – 4 = 3x – 6
y – 4 – 3x + 6 = 0
y – 3x + 2 = 0
Jawaban B

1. 3y + 4x – 4 = 0
2. 2y + 4x – 4 = 0
3. 2y – 4x + 4 = 0
4. 3y – 4x – 4 = 0

PEMBAHASAN :
Menentukan persamaan garis lurus dari dua titik yang diketahui menggunakan rumus:



3(y – 4) = 4(x – 2)
3y – 12 = 4x – 8
3y – 4x – 12 + 8 = 0
3y – 4x – 4 = 0
Jawaban D

PEMBAHASAN :
Menentukan titik potong dapat dicari dengan menentukan nilai x dan y melalui penyelesaian sistem persamaan linear dua variabel
Menentukan y dengan mengeliminasi x

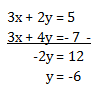
Menentukan x dengan mensubstitusikan nilai y ke salah satu persamaan
3x + 2y = 5
3x + 2(-6) = 5
3x – 12 = 5
3x = 5 + 12 = 17
x =
Maka koordinat titik potongnya adalah

Jawaban C

PEMBAHASAN 
Titik (4, a) dilalui garis 4x – 6y = 8, substitusikan titik tersebut ke persamaan garis
4.4 – 6.a = 8
16 – 6a = 8
-6a = 8 – 16 = 8
a =
Jawaban B

1. y + x – 4 = 0
2. 2x – y – 2 = 0
3. x + 2y – 5 = 0
4. x – y – 2 = 0

PEMBAHASAN :
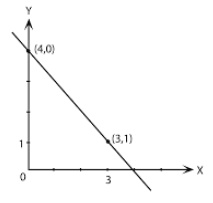
Dari gambar diketahui persamaan garis melalui dua titik yaitu (4, 0) dan (3, 1). Maka persamaan garisnya dapat ditentukan dengan rumus:


y = -(x -4)
y = -x + 4
y + x – 4 = 0
Jawaban A

1. 1
2. 2
3. 3
4. 4

PEMBAHASAN :
Persamaan garisnya  y = 2x – 7
Absis = titik pada sumbu x = 5
Ordinat = titik pada sumbu y

Maka untuk mencari nilai ordinat, substitusikan nilai x pada persamaan garis sebagai berikut:
y = 2x -7
y = 2(5) – 7
y = 3
Jawaban C

PEMBAHASAN :
Gradien adalah nilai yang dihasilkan dari perbandingan ordinat dan absis yang menyatakan kemiringan suatu garis. Pada persamaan garis y = mx, gradien sama dengan koefisien variable x. sehingga gradien pada persamaan 5y = 3x sebagai berikut:
5y = 3x

Jawaban C

PEMBAHASAN :
Persamaan garis ubah ke bentuk y = mx + c, sehingga diperoleh:
3y – 2x + 18 = 0
3y = 2x – 18

Jawaban A

1. (1,12)
2. (3,6)
3. (4,2)
4. (2,9)

PEMBAHASAN :
Untuk menyelesaikan soal di atas adalah dengan menguji pilihan satu persatu, sebagai berikut:

1. Koordinat (1,12)
   x = 1
   y = 15 – 3x
   y = 15 – 3(1)
   y = 12
   (1,12) (dilalui)
2. Koordinat (3,6)
   x = 3
   y = 15 – 3x
   y = 15 – 3(3)
   y = 6
   (3,6) (dilalui)
3. Koordinat (4,2)
   x = 4
   y = 15 – 3x
   y = 15 – 3(4)
   y = 3
   (4,3) (tidak dilalui)
4. Koordinat (2,9)
   x = 2
   y = 15 – 3x
   y = 15 – 3(2)
   y = 9
   (2,9) (dilalui)

Jawaban C

1. 6x – 2y + 4 = 0
2. 4x – 3y + 6 = 0
3. 8y + 6x – 12 = 0
4. 3y + 4x – 6 = 0

PEMBAHASAN :
Untuk mengetahui persamaan garis dengan gradien (m) = 4/3 adalah dengan mengubah persamaan menjadi y = mx + c dan mengujinya satu persatu sebagai berikut:

1. 6x – 2y + 4 = 0
   6x + 4 = 2y
   y = 3x + 2
   m = 3
2. 4x – 3y + 6 = 0
   4x + 6 = 3y
   
3. 8y + 6x – 12 = 0
   8y = – 6x + 12
   4y = – 3x + 6
   
4. 3y + 4x – 6 = 0
   3y = – 4x + 6
   

Maka jawaban yang tepat adalah jawaban pilihan B
Jawaban B

1. (-1,-4) dan (1,4)
2. (1,3) dan (3,1)
3. (2,3) dan (2,-5)
4. (1,5) dan (3,5)

PEMBAHASAN :
Apabila terdapat garis yang sejajar dengan sumbu x, maka gradiennya adalah nol (m = 0), maka berlaku rumus sebagai berikut:

1. (-1,-4) dan (1,4)
   
2. (1,3) dan (3,1)
   
3. (2,3) dan (2,-5)
   
4. (1,5) dan (3,5)
   

Maka jawaban yang tepat adalah jawaban pilihan D
Jawaban D

1. ½
2. 2
3. -1
4. 1

PEMBAHASAN :
Hasil kali gradien dari dua garis yang saling tegak lurus = -1
Maka gradien garis B dapat dihitung sebagai berikut:
m_A x m_B = -1
-2 x m_B = -1

Jawaban A

1. -1
2. 0
3. Tidak memiliki gradien
4. 1

PEMBAHASAN :
Apabila suatu garis sejajar dengan sumbu y maka garis tersebut tidak memiliki gradien. Garis y = 5 sejajar sumbu y.
Jawaban C

1. 1
2. -3
3. 0
4. -6

PEMBAHASAN :
Gradien  yang melalui dua titik, titik (2,1) dan titik (3,-5)  maka rumus  gradien yang berlaku sebagai berikut:

Jawaban D

1. 2y – 3x + 6 = 0
2. 2y – x – 4 = 0
3. 2y + x – 10 = 0
4. y – 6x – 5 = 0

PEMBAHASAN :
Menentukan gradien garis B:
3y + 6x – 12 = 0
⇔ 3y = – 6x + 12
⇔ y = – 2x + 4

Maka gradien garis B = – 2
Hasil kali gradien dari dua garis yang saling tegak lurus = -1
Maka gradien garis A dapat dihitung sebagai berikut:
m_A x m_B = -1
m_A x -2 = – 1
m_A = ½

Untuk persamaan garis A yang melewati titik (2,3) berlaku  rumus sebagai berikut:
y – y₁ = m (x – x₁ )
y – (3) = ½ (x – 2)
y – 3 = ½ x – 1
y = ½ x + 2
dikalikan 2, menjadi:
2y – x – 4 = 0
Jawaban B

1. y = 4x – 13
2. y = 2x + 5
3. y = 6x – 5
4. y = 3x – 2

PEMBAHASAN :
Dua garis yang sejajar memiliki gradien yang sama:
Persamaan garis :
y = 4x + 9
m = 4

Untuk persamaan garis yang melewati titik (2,-5)dengan m = 4 berlaku  rumus sebagai berikut:
y – y₁ = m (x – x₁ )
y – (- 5) = 4 (x – 2)
y + 5 = 4x – 8
y = 4x – 13
Jawaban A

1. y = 2x + 5
2. y = – 5x +3
3. y = -3x + 5
4. y = x + 13

PEMBAHASAN :
Persamaan garis lurus melalui dua titik yaitu (1,2) dan (3, -4). Apabila diketahui dua titik koordinatnya. Rumus yang berlaku  adalah sebagai berikut:

Jawaban C

1. – 1/3
2. 1/2
3. -1
4. 2/3

PEMBAHASAN :
Hasil kali gradien dari dua garis yang saling tegak lurus = -1
2y = 6x + 10
Dibagi 2
y = 3x + 5
m₁ = 3

Maka gradien garis yang saling tegak lurus tersebut  dapat dihitung sebagai berikut:
m₁ x m₂ = -1
3 x m₂ = -1
m₂= – 1/3
Jawaban A

1. y = 2x
2. y = x + 3
3. y = 2x – 5
4. y = – 3x – 2

PEMBAHASAN :
Persamaan garis lurus melalui dua titik yaitu (2,5) dan (-2, 1). Apabila diketahui dua titik koordinatnya. Rumus yang berlaku  adalah sebagai berikut:

Jawaban B

1. 1/3
2. – 1/2
3. 1/6
4. -1

PEMBAHASAN :
Gradien  yang melalui dua titik  (-4,3) dan (2,4) maka rumus  gradien yang berlaku sebagai berikut:

Jawaban C