Contoh Soal & Pembahasan Persamaan & Pertidasamaan Linear Satu Variabel & Dua Variabel SMP
PEMBAHASAN :
4x + 7 = 12
⇔ 4x = 12 – 7 = 5
⇔ x = ![]()
Jawaban A
- -3
- -2
- -1
- 0
PEMBAHASAN :
6(3x+2) + 4 = 4x + 2
⇔ 18x + 12 + 4 = 4x + 2
⇔ 18x + 16 = 4x + 2
⇔ 18x – 4x = 2 – 16
⇔ 14x = -14
![]()
Jawaban C
- 1
- 2
- 3
- 4
PEMBAHASAN :
![]()
4x + 2 = 3 x 6
⇔ 4x + 2 = 18
⇔ 4x = 18 – 2 = 16
![]()
Jawaban D
Umur Anaya 3 kali umur Zaki. Jika umur Anaya 8 tahun lebih tua dari Zaki maka umur Zaki sekarang adalah….
- 4 tahun
- 5 tahun
- 6 tahun
- 7 tahun
PEMBAHASAN :
Jika dimisalkan umur Zaki adalah x
maka dapat dituliskan sebagai berikut
3x = x + 8
⇔ 3x – x = 8
⇔ 2x = 8
![]()
Jawaban A
- x < 1
- x > 1
- x < 2
- x > 2
PEMBAHASAN :
3(4x + 2) – (x – 3) < 8x + 3
⇔ 12x + 6 – x + 3 < 8x + 3
⇔ 11x + 9 < 8x + 3
⇔ 11x – 8x < 3 – 9
⇔ 3x < 6
⇔ x < 2
Jawaban C
- x < -1
- x > -1
- x < -2
- x > -2
PEMBAHASAN :
![]() ………….kalikan 6
………….kalikan 6
⇔ 2x – 18x < 8
⇔ -16x < 16
⇔ -x < 1 (dibagi -1, tanda dibalik) ⇔ x > -1
Jawaban B
- -9
- -3
- 7
- 11
PEMBAHASAN :
Menentukan nilai x dengan cara eliminasi y
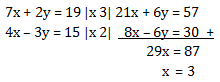
Menentukan y dengan mensubstitusikan x ke salah satu persamaan
7x + 2y = 19
⇔ 7.3 + 2y = 19
⇔ 21 + 2y = 19
⇔ 2y = 19 – 21 = -2
⇔ y = -1
Maka
3x – 2y = 3.3 – 2.(-1) = 9 – (-2) = 9 + 2 = 11
Jawaban D
- Rp. 1.000
- Rp. 3.000
- Rp. 7.000
- Rp. 10.000
PEMBAHASAN :
Jika dimisalkan
harga mangga = x
harga jeruk = y
Menentukan harga mangga (x) dengan mengeliminasi y
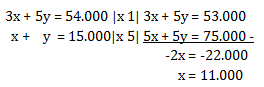
Menentukan harga jeruk (y) dengan mensubstitusikan x ke salah satu persamaan
x + y =15.000
⇔ 11.000 + y = 15.000
⇔ y = 15.000 – 11.000 = 4.000
Maka selisih harga mangga dan jeruk
x – y = 11.000 – 4.000 = Rp. 7.000
Jawaban C
- 12
- 14
- 16
- 18
PEMBAHASAN
Jika dimisalkan:
![]()
![]()
maka persamaan menjadi
2x + 3y = ![]() ……dikalikan 4
……dikalikan 4
8x + 12y = 3…………pers (1)
3x + 2y = ![]() ………..dikalikan 3
………..dikalikan 3
9x + 6y = 4 …………..pers (2)
Menentukan x dengan mengeliminasi x
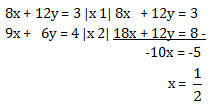
Menentukan y dengan mensubstitusikan x ke salah satu percobaan
8x + 12y = 3
⇔ 8.½ + 12y = 3
⇔ 4 + 12y = 3
⇔ 12 y = 3 – 4 = -1
![]()
maka nilai a dan b
![]()
a = 2
![]()
b = 12
Sehingga
a – b = 2 – (-12) = 2 + 12 = 14
Jawaban B
PEMBAHASAN :
Menentukan x dengan mengeliminasi x
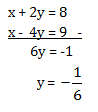
Menentukan x dengan cara mensubstitusikan y ke salah satu persamaan
x + 2y = 8
x + 2.![]() = 8
= 8
x + ![]() = 8
= 8
x – ![]() = 8
= 8
x = 8 + ![]() =
= ![]()
Maka himpunan penyelesaiannya : ![]()
Jawaban B
- =
- >
- <
- ≤
PEMBAHASAN :
Kalimat terbuka ada dua jenis yaitu:
- Persamaan: kalimat terbuka yang dihubungkan dengan tanda sama dengan (=)
- Pertidaksamaan : kalimat terbuka yang dihubungkan dengan tanda >, ≥, <, dan ≤
Jawaban A
- =
- >
- <
- ≤
PEMBAHASAN :
Kalimat terbuka ada dua jenis yaitu:
- Persamaan: kalimat terbuka yang dihubungkan dengan tanda sama dengan (=)
- Pertidaksamaan : kalimat terbuka yang dihubungkan dengan tanda >, ≥, <, dan ≤
Jawaban A
- x > y + 3
- x + 2 = – 10
- 2x – y = 15
- x – 7 < 1
PEMBAHASAN :
- x > y + 3 → pertidaksamaan linear dua variabel
- x + 2 = – 10 → persamaan linear satu variabel
- 2x – y = 15 → persamaan linear dua variabel
- x – 7 < 1 → pertidaksamaan linear satu variabel
Jawaban C
- – 8 – 6 = 2
- 5 + 1 > 4
- 2x – y = 2xy
- x + 5 = 10
PEMBAHASAN :
- – 8 – 6 = 2 → salah – 8 – 6 = 14
- 5 + 1 > 4 → benar 6 > 4
- 2x – y = 2xy → nilai x dan y belum diketahui, benar/ salah belum diketahui
- x + 5 = 10 → nilai x belum diketahui, benar/salah belum diketahui
Jawaban B
- 2
- 3
- 4
- 5
PEMBAHASAN :
x = {1,3,5,7, …}
Untuk mengetahui nilai x dapat dilakukan pengujian pada setiap pilihan sebagai berikut:
x = 1 → 3x – 2 = 13 → 3.1 – 2 ≠ 13
x = 3 → 3x – 2 = 13 → 3.2 – 2 ≠ 13
x = 5 → 3x – 2 = 13 → 3.5 – 2 = 13 (memenuhi)
x = 7 → 3x – 2 = 13 → 3.7 – 2 ≠ 13
Jawaban D
- x = – 5
- x = 5
- x = 1
- x = 11
PEMBAHASAN :
5x – 7 = 18
5x = 25
x = 5
himpunan penyelesiannya adalah x = 5
Jawaban B
- 8
- 10
- 12
- 15
PEMBAHASAN :
![]() x = 8
x = 8
Ruas kiri dan ruas kanan dikalikan 3, sehingga diperoleh:
2x = 24
x = 12
Jawaban C
- -3
- 1
- 2
- -2
PEMBAHASAN :
2(4x + 2) + 6 = 2x – 8
8x + 4 + 6 = 2x – 8
8x + 10 = 2x – 8
6x = – 18
x = – 3
Jawaban A
- x = – 1
- x = 2
- x = 4
- x = 3
PEMBAHASAN :
11x – 18 = 6x + 2
11x – 6x = 2 + 18
5x = 20
x = 4
Jawaban C
- 2
- -3
- 4
- -1
PEMBAHASAN :
![]()
Ruas kiri dan ruas kanan dikalikan 6
4a + 2 = 18
4a = 16
a = 4
Jawaban C
- 1
- 2
- 3
- 4
PEMBAHASAN :
Misalkan variabelnya adalah x, diperoleh persamaan:
3x – 1 = 11
Ruas kiri dan ruas kanan ditambah 1
3x – 1 + 1 = 11 + 1
3x = 12
x = 4
Jawaban D
- Rp 750.000,00
- Rp 500.000,00
- Rp 1.000.000,00
- Rp 950.000,00
PEMBAHASAN :
Persamaan 1
x = 3y
Persamaan 2
x = y + 500.000
Substistusikan persamaan 1 ke persamaan 2
x = y + 500.000
3y = y + 500.000
2y = 500.000
y = 250.000
Maka jumlah uang karyawan x sebagai berikut:
x = 3y
x = 3(250.000)
x = 750.000
Jawaban A
- {0,1,2}
- {1,2,3}
- {1,2}
- {3,4,5, …}
PEMBAHASAN :
3x – 5 < 4 dengan x ∈ {1,2,3,4, …}
⇔ 3x – 5 < 4
⇔ 3x < 4 + 5
⇔ 3x < 9
⇔ x < 3
Maka nilai x yang memenuhi adalah {1,2}
Jawaban C
- x ≤ 10
- x ≤ 11
- x ≥ – 9
- x ≥ 8
PEMBAHASAN :
3x – 6 ≤ 2x + 5
3x – 2x ≤ 5 + 6
x ≤ 11
Maka penyelesaiannya adalah x ≤ 11
Jawaban B
- a > 5
- a > – 8
- a < -10
- a < 13
PEMBAHASAN :
![]()
Ruas kiri dan ruas kanan dikalikan 3, maka diperoleh:
⇔ 4a – 7 < 3a + 6
⇔ 4a – 3a < 6 + 7
⇔ a < 13
Maka penyelesaiannya adalah a < 13
Jawaban D
PEMBAHASAN :
5x – 12 < 2(3x + 4)
5x – 12 < 6x + 8
5x – 6x < 8 + 12
-x < 20
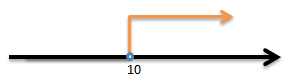
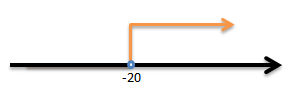
x > 20
Gambarkan x > 20 pada garis bilangan:
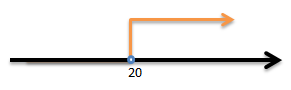
Jawaban C
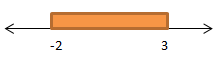
- -2
- -1
- 0
- 2
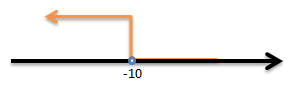
PEMBAHASAN :
Pertidaksamaan yang sesuai dengan gambar garis bilangan di atas adalah -2 < x < 3 dan anggotanya yaitu {-1,0,2}
Jawaban A
- x < 1
- x < – 4
- x > 3
- x > -3
PEMBAHASAN :
![]()
Ruas kiri dan ruas kanan dikalikan 12 diperoleh pertidaksamaan sebagai berikut:
4(2x ) – 3(3x ) < 3(1)
8x – 9x < 3
-x < 3
x > 3
Jawaban C
- x ≥ -7
- x ≥ 7
- x ≤ 3
- x ≤ -3
PEMBAHASAN :
3a – 2(a + 1) ≤ 2a + 5
3a – 2a – 2 ≤ 2a + 5
a – 2 ≤ 2a + 5
a – 2a ≤ 5 + 2
-a ≤ 7
a ≥ 7
Jawaban B
- a > 1/3
- a > 1/4
- a > 1/5
- a > 1/6
PEMBAHASAN :
3(x – 2) + (5x – 1) > 2(x – 3)
⇔ 3x – 6 + 5x – 1 > 2x – 6
⇔ 8x – 7 > 2x – 6
⇔ 8x – 2x > – 6 + 7
⇔ 6x > 1
⇔ x > 1/6
Jawaban D
- 5
- – 5
- 6
- 7
PEMBAHASAN :
3x + 3y = 15 | x 4 | 12x + 12y = 60
4x + 3y = 24 | x 3 | 12x + 9y = 72
⇔ 3y = – 12
⇔ y = – 4
Menentukan nilai x sebagai berikut:
3x + 3y = 15
⇔ 3x + 3(-4) = 15
⇔ 3x – 12 = 15
⇔ 3x = 15 + 12
⇔ 3x = 27
⇔ x = 9
Jadi x + y = 9 + (- 4) = 5
Jawaban A
- 315
- 420
- 280
- 300
PEMBAHASAN :
Diketahui:
Keliling = 72 cm
p – l = 6 cm
Rumus keliling = 2 (p + l)
72 = 2 (p + l)
36 = p + l …….. persamaan 1
6 = p – l ………. persamaan 2
Maka diperoleh system persamaan linear sebagai berikut:
p + l = 36
p – l = 6
2p = 42
p = 21
⇔ P + l = 36
⇔ 21 + l = 36
⇔ l = 15
Jadi luas persegi panjang dapat dihitung sebagai berikut:
Luas persegi panjang = p x l = 21 x 15 = 315 cm2
Jawaban A
- 36
- 16
- 56
- 20
PEMBAHASAN :
Misalkan dua bilangan bulat tersebut adalah a dan b
Sehingga diperoleh persamaan linear sebagai berikut:
a – b = 16
a + b = 56
2a = 72
a = 36
Maka nilai b dapat dihitung sebagai berikut:
a – b = 16
36 – b = 16
-b = -20
b = 20
jadi bilangan terkecil adalah 20
Jawaban D
- 26
- 30
- 24
- 32
PEMBAHASAN :
Diketahui:
Jarak tempuh perjalanan = 212 km
Kecepatan awal = (2a + 12) km/jam, waktu tempuh = 2 jam
Kecepatan selanjutnya = (2a + 18) km/jam, waktu tempuh = 5 jam
Rumus jarak = waktu x kecepatan
Diperoleh persamaan linear sebagai berikut:
212 = 2(2a + 12) + 5(2a + 18)
212 = 4a + 24 + 10a + 90
212 = 14a + 114
14a = 212 – 114
14a = 98
a = 7
Maka kecepatan awal kendaraan dapat dihitung sebagai berikut:
Kecepatan awal = 2a + 12
⇔ 2a + 12
⇔ 2(7) + 12
⇔ 14 + 12
⇔ 26 km/jam
Jawaban A
- 14
- -14
- 11
- -11
PEMBAHASAN :
2x + 4y = 10 | x 3 | 6x + 12y = 30
3x – 3y = 42 | x 2 | 6x – 6y = 84
18y = – 54
y = – 3
Menentukan nilai x sebagai berikut:
2x + 4y = 10
2x + 4(-3) = 10
2x – 12 = 10
2x = 22
x = 11
Maka nilai x – y = 11 – ( – 3) = 14
Jawaban A
- 5
- 10
- 20
- 15
PEMBAHASAN :
2p – 3q = 50 | x 1 | 2p – 3q = 50
p + 2q = 18 | x 2 | 2p + 4q = 36
-7q = 14
q = -2
Menentukan nilai p sebagai berikut:
p + 2q = 18
p + 2(-2) = 18
p – 4 =18
p = 22
Maka p + q = 22 + (-2) = 20
Jawaban C
- 10
- 14
- 16
- 18
PEMBAHASAN :
- 2x + 3y = 28
- x + 2y = 12 → x = 12 – 2y
Substitusikan persamaan 2 ke persamaan 1 sebagai berikut:
2x + 3y = 28
2(12 – 2y) =28
24 – 4y = 28
-4y = 28 – 24
-4y = 4
y = – 1
Menentukan nilai x sebagai berikut:
x = 12 – 2y
x = 12 – 2(-1)
x = `12 + 2
x = 14
Jawaban B
- ½
- 3
- 3/2
- 6
PEMBAHASAN :
3a + 2b = 10
5a – 2b = 14
8a = 24
a = 3
Menentukan nilai b sebagai berikut:
3a + 2b = 10
3(3) + 2b = 10
9 + 2b = 10
2b = 1
b = ½
Maka a : b = 3 : ½ = 6
Jawaban D
- 244
- 289
- 324
- 378
PEMBAHASAN :
Diketahui:
Keliling = 72 cm
Panjang sisinya = (p + 2) cm
Rumus keliling persegi = 4 x sisi
72 = 4 x (p + 2)
72 = 4p + 8
4p = 72 – 8
4p = 64
P = 16
Panjang sisi = p + 2 = 16 + 2 = 18 cm
Maka luas persegi = sisi x sisi = 18 x 18 = 324 cm2
Jawaban C
- 2
- – 1
- – 2
- 3
PEMBAHASAN :
5(2x + 1) – (3x – 2) = 2x + 6
10x + 5 – 3x + 2 = 2x + 6
7x + 7 = 2x + 6
5x = – 1
x = – 1/5
Maka nilai x . 5 = – 1/5 . 5 = – 1
Jawaban B
- x > 5
- x > 4
- x < 3
- x < 2
PEMBAHASAN :
4x + 2 – x > 2(x + 5) – 3
3x + 2 > 2x + 10 – 3
3x + 2 > 2x + 7
x > 5
Jawaban A
- {0, 1 }
- {0, 1, 2}
- {0, 1, 2, 3}
- {0, 1, 2, 3, 4}
PEMBAHASAN :
3x – 10 < – 1 , x ∈ {0, 1, 2, 3, 4, 5, … }
3x – 10 < – 1
3x < 9
x < 3
Maka nilai x yang memenuhi adalah {0, 1, 2}
Jawaban B
- x ≤ 5
- x ≥ – 7
- x ≤ – 3
- x ≤ 8
PEMBAHASAN :
3x – 12 ≤ 2x – 4
3x -2x ≤ – 4 + 12
x ≤ 8
Maka penyelesaiannya adalah x ≤ 8
Jawaban D
- d < 12
- d > 12
- d = 10
- d < -12
PEMBAHASAN :
![]() → kalikan dengan 3
→ kalikan dengan 3
2d – 10 < d + 2
2d – d < 2 + 10
d < 12
Maka penyelesaiannya adalah d < 12
Jawaban A
- x < 2
- x < -2
- x > 2
- x > -2
PEMBAHASAN :
(3x – 1) – 2(x + 1) < 2x – 5
3x – 1 – 2x – 2 < 2x – 5
x – 3 < 2x – 5
x – 2x < – 5 + 3
– x < – 2
x < 2
Maka penyelesaiannya adalah x < 2
Jawaban A
- x > – 5
- x > 5
- x < -5
- x < 5
PEMBAHASAN :
![]() → kalikan dengan 6
→ kalikan dengan 6
2(x + 6) – (3x + 3) < 2(2)
2x + 12 – 3x – 3 < 4
-x + 9 < 4
-x < 4 – 9
-x < -5
x < 5
Jawaban D
- 5 kg
- 2,5 kg
- 1 kg
- 3 kg
PEMBAHASAN :
Misalkan berat badan Ayu adalah p
Berdasarkan soal di atas kalimat matematikanya sebagai berikut:
3p = p + 6
3p – p = 6
2p = 6
p = 3
Maka berat badan Ayu adalah 3kg
Jawaban D
- 5
- 10
- 15
- 20
PEMBAHASAN :
Misalkan bilangan tersebut adalah x, sehingga diperoleh persamaan sebagai berikut:
3x + 5 = 35
3x = 35 – 5
3x = 30
x = 10
Maka bilangan tersebut = x = 10
Jawaban B
- x > 19
- x > – 19
- x ≤ 11
- x ≤ – 11
PEMBAHASAN :
(2x – 1) + 3(x – 2) > 4(x + 3)
2x – 1 + 3x – 6 > 4x + 12
5x – 7 > 4x + 12
5x – 4x > 12 + 7
x > 19
Maka penyelesaiannya adalah x > 19
Jawaban A
- 144
- 225
- 529
- 441
PEMBAHASAN :
Diketahui:
Keliling persegi = 92 cm
Panjang sisi = (x + 2) cm
Rumus keliling persegi = 4 x s
4(x + 2) = 92
4x + 8 = 92
4x = 92 – 8
4x = 84
x = 21
Panjang sisi = x + 2 = 21 + 2 = 23 cm
Rumus luas persegi = s x s
= 23 cm x 23 cm
= 529 ![]()
Jawaban C
- =
- ⇔
- ≅
- ∼
PEMBAHASAN :
Persamaan ekuivalen adalah dua persamaan yang memiliki penyelesaian sama, dilambangkan dengan ” ⇔ ”
Jawaban B