DAFTAR ISI
Rangkuman Materi Statistika Kelas 8
Perumusan Ukuran Statistika
Perumusan ukuran statistika dibedakan menjadi 2 jenis data, yaitu:
Data tunggal
Data yang diruliskan dengan mendaftar satu per satu
Data kelompok
Data yang dituliskan dengan bentuk interval kelas.
Ukuran Pemusatan
Ukuran statistik yang dapat menjadi pusat dari rangkaian data dan memberi gambaran singkat tentang data, terdiri dari tiga bagian yaitu mean, median dan modus
Mean (Rataan Hitung)
Merupakan ukuran pemusatan atau rata-rata hitung
Mean data tunggal
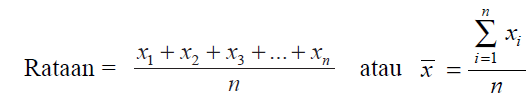
Keterangan:
∑x = jumlah data
n = banyaknya data
xi = data ke-i
Mean data distribusi frekuensi
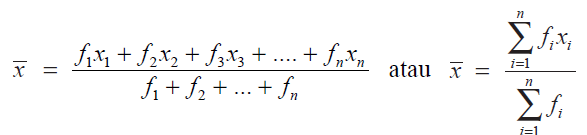
Keterangan:
fi = frekuensi untuk nilai xi
xi = data ke-i
Mean data kelompok
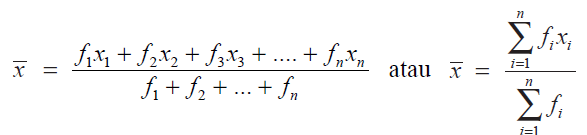
Keterangan:
fi = frekuensi untuk nilai xi
xi = titik tengah rentang tertentu
Cara lain:
- Menentukan rataan sementaranya.
- Menentukan simpangan (d) dari rataan sementara.
- Menghitung simpangan rataan baru dengan rumus berikut ini.
- Menghitung rataan sesungguhnya.
Median (Me)
Merupakan suatu nilai tengah yang telah diurutkan
Median data tunggal
Data ganjil: ambil nilai yang berada di tengah
Data genap: ambil rata rata dua data yang berada di tengah
Median data kelompok

Ket:
L2 = tepi bawah kelas median
n = banyak data
(∑f)2 = jumlah frekuensi sebelum kelas median
f2 = frekuensi kelas median
c = panjang interval kelas
Modus (Mo)
Merupakan nilai yang paling sering muncul atau nilai yang mempunyai frekuensi tertinggi
Modus data tunggal
Ambil data yang jumlahnya paling banyak
Modus data kelompok
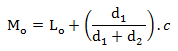
Ket :
L0= Tepi bawah kelas modus
d1= selisih frekuensi kelas modus dengan frekuensi kelas sebelum modus
d2= selisih frekuensi kelas modus dengan frekuensi kelas sesudah modus
c = panjang interval kelas
Ukuran Letak
Ukuran letak meliputi kuartil (Q), desil (D), dan Persentil (P).
Kuartil (Q)
Membagi data yang telah menjadi empat bagian yang sama banyak
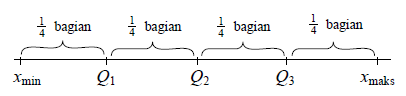
Keterangan:
xmin = data terkecil
xmaks = data terbesar
Q1 = kuartil ke-1
Q2 = kuartil ke-2
Q3 = kuartil ke-3
Kuartil data tunggal
![]()
Keterangan:
Qi = kuartil ke-i
n = banyak data
Kuartil data kelompok
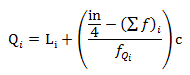
Keterangan:
Qi = kuartil ke-i (1, 2, atau 3)
Li = tepi bawah kelas kuartil ke-i
n = banyaknya data
(∑f)i = frekuensi kumulatif kelas sebelum kelas kuartil
c = lebar kelas
f = frekuensi kelas kuartil
Desil dan persentil
Desil membagi data menjadi sepuluh bagian yang sama besar. Sedangkan persentil membagi data menjadi 100 bagian yang sama.
Desil dan persentil data tunggal
Desil
![]()
Keterangan:
Di = desil ke-i
i = 1, 2, 3, . . ., 9
n = banyaknya data
Persentil
![]()
Keterangan:
Pi = persentil ke-i
i = 1, 2, 3, . . ., 99
n = banyaknya data
Ukuran Penyebaran
menggambarkan penyebaran data tersebut dan dapat dikaitkan dengan simpangan (lebar data) dari suatu nilai tertentu. Contoh : jangkauan, hamparan, simpangan, quartil, dan simpangan rata-rata
Jangkauan (J)
Selisih antara data terbesar dengan data terkecil
Jangkauan data tunggal
J = xmaks - xmin
Jangkauan data kelompok
J = nilai tengah kelas tertinggi - nilai tengah kelas terendah
Hamparan (Jangkauan antar kuartil) (R)
Selisih antara kuartil atas dengan kuartil bawah
Hamparan untuk data tunggal dan kelompok:
R = Q2 - Q1
Keterangan:
Q2 = kuartil atas
Q1 = kuartil bawah
Simpangan kuartil (Qd)
Simpangan antar kuartil
Simpangan antar kuartil untuk data tunggal dan kelompok:
Qd = (Q3 – Q1 )
Simpangan rata rata
Simpangan terhadap rata rata
Simpangan rata-rata data tunggal
![]()
Keterangan:
SR = simpangan rata-rata
n = ukuran data
xi = data ke-i dari data x1, x2, x3, …, xn
x = rataan hitung
Simpangan rata-rata data kelompok
Simpangan baku
akar dari jumlah kuadrat deviasi dibagi banyaknya data
Simpangan baku data tunggal
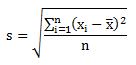
Keterangan: n = banyaknya data
Simpangan baku data kelompok
Ragam/Variasi
Ragam data tunggal

Keterangan: n = banyaknya data
Ragam data kelompok
![]()
Keterangan: n = banyaknya data
Contoh Soal & Pembahasan Statistika & Peluang Kelas VIII SMP
- 5
- 6
- 7
- 8
PEMBAHASAN :
Jumlah data nilai siswa adalah 9
Diketahui rata-rata nilai siswa adalah 6,23, maka nilai x adalah
![]()
![]()
6,23 x 9 = 50 + x
56 = 50 + x
x = 56 - 50 = 6
Jawaban B
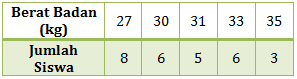
- 27
- 30
- 31
- 33
PEMBAHASAN :
Modus merupakan data yang paling sering muncul atau yang frekuensi kemunculannya terbesar. Dari data di soal maka berat badan yang paling banyak ada di siswa adalah 27 kg sebanyak 8 siswa. Maka modusnya adalah 27
Jawaban A
- 26
- 27
- 28
- 29
PEMBAHASAN :
Median adalah nilai yang tepat ditengah-tengah jika data diurutkan dari yang terkecil ke yang terbesar. Jika data nya ganjil maka median adalah nilai yang tepat di tengah-tengah. Jika data nya genap maka median merupakan rata-rata data yang ditengah.
Data di soal jika diurutkan dari terkecil ke terbesar
23, 25, 25, 26, 27, 27, 28, 29, 30, 30, 31, 32, 33, 33, 34
Karena datanya ada 15 (ganjil) maka mediannya tepat ditengah-tengah yaitu 29
Jawaban D
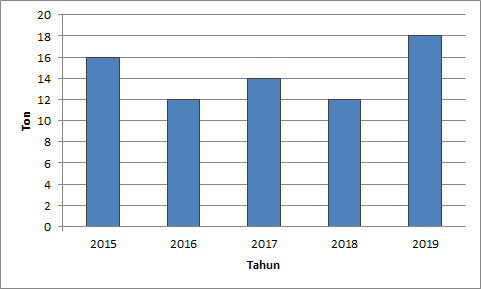
Diketahui grafik di bawah ini
- 11,3
- 12,5
- 14,4
- 15,2
PEMBAHASAN :
Dari grafik dapat ditentukan bahwa jumlah tahun adalah 5 tahun (jumlah data) dengan data sebagai berikut:
2015 : 16 ton
2016 : 12 ton
2017 : 14 ton
2018 : 12 ton
2019 : 18 ton
Maka rata-rata hasil panen selama 5 tahun adalah
![]()
![]()
Jawaban C
- 5,32
- 5,65
- 6,67
- 7,5
PEMBAHASAN :
Mean sama dengan nilai rata-rata, maka nilai meannya adalah
![]()
![]()
Jawaban C
PEMBAHASAN :
Jumlah kelereng = 24 kelereng
Jumlah kelereng bukan biru = 15 + 4 = 19 kelereng
Maka peluang terambilnya kelereng bukan biru adalah
![]()
Jawaban B
- 2 kali
- 4 kali
- 6 kali
- 8 kali
PEMBAHASAN :
Peluang pemanah gagal mengenai titik di tengah papan sasaran adalah 1 - 0,8 = 0,2
Maka jumlah pemanah tersebut gagal tepat sasaran jika melakukan 30 kali percobaan adalah
30 kali x 0,2 = 6 kali gagal
Jawaban C
- ¼
- ½
- ¾
- 1/3
PEMBAHASAN :
Menentukan frekuensi relatif yaitu dengan membandingkan jumlah yang muncul dengan jumlah kejadian, maka frekuensi relatif munculnya mata dadu 6 adalah
![]()
Jawaban A
- 14/32
- 9/16
- 7/16
- 15/16
PEMBAHASAN
Jumlah siswa total = 14 + 18 = 32 orang
maka peluang siswa perempuan yang menjadi ketua murid adalah
![]()
Jawaban B
- 1/6
- 1/8
- 1/9
- 1/7
PEMBAHASAN :
Jika tiga mata uang dilempar bersamaan maka ruang sampelnya adalah {(AAA), (GGG), (AGG), (GAG), (GGA), (AAG), (AGA), (GAA)}. sisi angka bersamaan muncul hanya satu kali dari 8 kali kemungkinan, maka peluangnya adalah ![]()
Jawaban B
- Ruang sampel: semua buah jeruk yang dimiliki penjual
Titik sampel: tiga jenis jeruk yang dibeli ibu - Ruang sampel: semua buah-buahan yang dimiliki penjual
Titik sampel: buah jeruk yang dibeli ibu - Ruang sampel: jenis-jenis jeruk
Titik sampel: jeruk yang tidak dibeli oleh ibu - Ruang sampel: jeruk yang tidak dibeli oleh ibu
Titik sampel: jeruk yang dibeli oleh ibu
PEMBAHASAN :
Ruang sampel adalah himpunan dari semua hasil kemungkinan yang akan muncul pada saat percobaan. Sedangkan titik sampel adalah setiap anggota dari ruang sampel.
Berdasarkan soal di atas yang merupakan ruang sampel adalah semua buah jeruk yang dimiliki penjual dan titik sampelnya adalah tiga jenis jeruk yang dibeli ibu.
Jawaban A
- Jeruk lemon memiliki rasa asam
- Deni menyukai olah raga basket
- Ahmad memiliki tinggi badan 170 cm
- Risa gemar minum susu
PEMBAHASAN :
Data kualitatif adalah data yang dijabarkan dengan kata-kata sedangkan data kuantitatif adalah data yang dijabarkan dengan angka-angka.
- Jeruk lemon memiliki rasa asam → data kualitatif
- Deni menyukai olah raga basket → data kualitatif
- Ahmad memiliki tinggi badan 170 cm → data kuantitatif
- Risa gemar minum susu → data kualitatif
Jawaban C
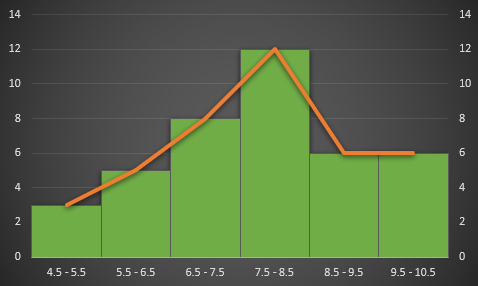
- Ogive
- Histogram
- Lingkaran
- Poligon
PEMBAHASAN :
Jenis-jenis bentuk diagram sebagai berikut:
- Ogive

Sumber gambar : Yos3prens.wordpress.com - Histogram

- Lingkaran

- Poligon

Jawaban D
Soal No.14
Perhatikan tabel di bawah ini!
Nama Hari | Jumlah Pengunjung Bioskop |
Senin | 96 |
Selasa | 101 |
Rabu | 99 |
Kamis | 112 |
Jumat | 135 |
Sabtu | 257 |
Minggu | 246 |
Kenaikan jumlah pengunjung terbanyak terjadi pada hari …
- Selasa
- Sabtu
- Jumat
- Kamis
PEMBAHASAN :
Nama Hari | Jumlah Pengunjung Bioskop | Jumlah Kenaikan/Penurunan Pengunjung |
Senin | 96 | - |
Selasa | 101 | +5 |
Rabu | 99 | -2 |
Kamis | 112 | +13 |
Jumat | 135 | +23 |
Sabtu | 257 | +122 |
Minggu | 246 | -11 |
Kenaikan pengunjung terbanyak terjadi pada hari sabtu
Jawaban B
- 5
- 6
- 7
- 8
PEMBAHASAN :
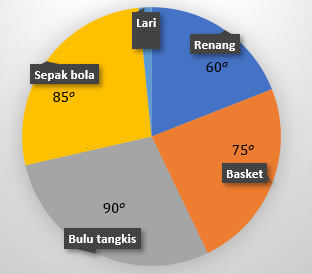
Diketahui:
Renang = 600
Basket = 750
Bulu tangkis = 900
Sepak bola = 850
Lari = 3600 – (600 + 750 + 800 + 850 ) = 3600 – 3000 = 600
Maka banyak siswa yang menyukai olah raga lari ![]()
Jawaban A
Nilai | Frekuensi |
3 | 13 |
5 | 7 |
7 | 9 |
4 | 6 |
8 | 10 |
Nilai rata-rata berdasarkan data di atas adalah …
- 6,18
- 5,36
- 6,72
- 4,24
PEMBAHASAN :
Banyak data = 13 + 7 + 9 + 6 + 10 = 45
Maka nilai rata- rata dapat dihitung sebagai berikut:
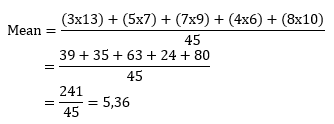
Jawaban B
- 5,5
- 7
- 8
- 6
PEMBAHASAN :
Jumlah nilai 10 orang siswa = 10 x 8,2 = 82
Jumlah nilai 10 + 1 orang siswa = 11 x 8 = 88
Maka nilai siswa baru = 88 – 82 = 6
Jawaban D
- 72 orang
- 64 orang
- 80 orang
- 120 orang
PEMBAHASAN :
Persentase pegawai swasta = 100% - (40% + 20% + 20%) = 20%
Jumlah pedagang = 40% x 120 = 48 orang
Jumlah pegawai swasta = 20% x 120 =24 orang
Jumlah pedagang dan pegawai swasta = 48 + 24 = 72 orang
Jawaban A
- 65
- 55
- 90
- 48
PEMBAHASAN :
Modus adalah nilai yang paling sering muncul, maka untuk mencarinya adalah sebagai berikut:
Tinggi Badan Balita (cm) | Banyak Balita |
65 | 2 |
76 | 1 |
55 | 3 |
90 | 4 |
48 | 2 |
83 | 1 |
102 | 1 |
89 | 1 |
88 | 1 |
100 | 1 |
80 | 1 |
68 | 1 |
75 | 1 |
Jumlah | 20 |
Sehingga modusnya adalah 90 cm
Jawaban C
Berat Badan Balita (kg) | Banyak Balita |
5 | 5 |
7 | 4 |
6 | 6 |
9 | 8 |
8 | 2 |
13 | 3 |
12 | 4 |
Jumlah | 32 |
Rata-rata berat badan siswa adalah … kg.
- 12
- 13
- 9
- 7
PEMBAHASAN :
Rata-rata berat badan balita dapat dihitung sebagai berikut:
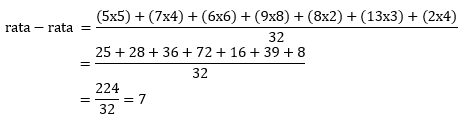
Jawaban D
- 13
- 6
- 12
- 9
PEMBAHASAN :
Modus adalah nilai yang paling sering muncul, lihat pada tabel di bawah ini!
Berat Badan Balita (kg) | Banyak Balita |
5 | 5 |
7 | 4 |
6 | 6 |
9 | 8 |
8 | 2 |
13 | 3 |
12 | 4 |
Jumlah | 32 |
Maka modusnya adalah 9 kg, terdapat 8 balita dengan berat badan 9 kg
Jawaban D
Data nilai 10 orang siswa yaitu 60, 85, 87, 92, 75, 65, 70, 90, 62, 76. Nilai tengah dari data tersebut adalah …
- 75,5
- 60,5
- 57,5
- 85,5
PEMBAHASAN :
Untuk mencari nilai tengah urutkan data dari nilai yang terkecil sampai nilai yang terbesar, sebagai berikut:
60, 62, 65, 70, 75, 76, 85, 87, 90, 92
1 2 3 4 5 6 7 8 9 10
Data berjumlah 10
Nilai tengah atau median terdapat pada urutan ke 5 dan 6, sehingga dapat dihitung sebagai berikut:
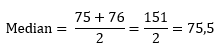
Jawaban A
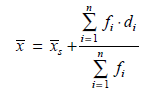

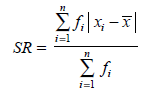
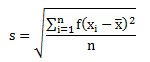
Terima kasih atas ilmunya Mas/Mbak 😀
Sangat bermanfaat