Contoh Soal & Pembahasan Statistika SMA Bagian II

Contoh Soal & Pembahasan Statistika Bagian II

Soal No.1

Diketahui nilai ulangan matematika siswa

Hitung rataan hitung, median dan modusnya

PEMBAHASAN :
Menentukan rataan hitung

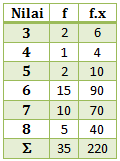
Menentukan median
Jumlah data/siswanya (n) = 35 (ganjil),

Mediannya nilai ke 18 jika diurut berdasarkan frekuensi maka nilai ke 18 adalah 5
Menentukan modus
Modus adalah nilai yang paling sering muncul atau frekuensinya paling banyak muncul. Maka modusnya yaitu nilai 6 sebanyak 15 kali

DOWNLOAD KUMPULAN SOAL CONTOH SOAL STATISTIKA SMA BAGIAN II DALAM BENTUK PDF KLIK DISINI

Soal No.2

Jika diketahui data:
4, 2, 2, 5, 4, 5, 3, 3, 6
Tentukan jangkauan semi interkuartil

PEMBAHASAN :
Jangkauan semi interkuartil atau simpangan kuartil adalah setengah dari jangkauan kuartil

Menentukan Q₁dan Q₃
dari data 4, 2, 2, 5, 4, 5, 3, 3, 6

Maka Q₁ = 2

Maka Q₃ = 3
Menentukan SQ
SQ = ½(Q₃ - Q₁) = ½ (3 -2) = ½

Soal No.3

Tentukan varians dari data berikut:
4,5, 6, 7, 3, 4, 5, 6, 3, 7, 3, 4, 5, 6, 7, 7, 5, 4, 6

PEMBAHASAN :

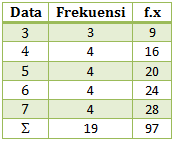
Menentukan rataan

B = 2 x 10^-3T
Periode yang diperlukan untuk menempuh satu lingkaran penuh:

dengan R adalah panjang jari-jari lintasan dengan rumusan

Maka waktu/periode yang ditempuh untuk setengah lingkaran adalah

Soal No.4
Dalam satu sekolah jika diambil 3 kelas dan dihitung rata-rata nilai matematikanya. Kelas IPA 1, IPA 2 dan IPA 3 memiliki jumlah siswa 35, 32, 34 dan diketahui rata-rata gabungan nilai matematikanya adalah 54,3. Jika rata-rata nilai kelas IPA 1 adalah 45 dan rata-rata kelas IPA 2 adalah 65. Tentukan rata-rata nilai kelas IPA 3!

PEMBAHASAN :
Menentukan rata-rata nilai matematika kelas IPA 3 dari rata-rata gabungan

Data Berikut untuk menjawab soal No 5 dan 6

Diketahui data no sepatu siswa dalam salah satu kelas sebagai berikut

Soal No.5
Tentukan mediannya

PEMBAHASAN :
Menentukan median
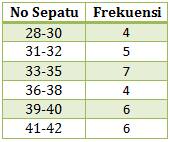
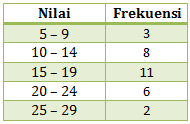
Median adalah nilai tengah, jika diurut berdasarkan frekuensi maka mediannya berada pada interval 33-35.

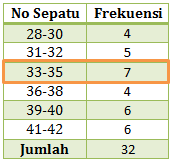
Diketahui:
tepi bawah (t_b) = 32,5
panjang interval kelas (c) = 3
Jumlah data (n) = 32
Jumlah frekuensi sebelum kelas median (Σ f_i) = 4 + 5 = 9
frekuensi median (f_q) = 7

Soal No.6

Dari data tabel di atas. Tentukan Modusnya

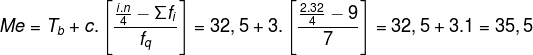
PEMBAHASAN :
Modus adalah data yang sering muncul. Jika dilihat dari frekuensi yang paling banyak. Maka modus ada pada interval: (33-35)
Diketahui:
tepi bawah (t_b) = 32,5
panjang interval kelas (c) = 3
frek kelas modus - frek kelas sebelum = d₁ = 7 - 5 = 2
frek kelas modus - frek kelas sesudah = d₂ = 7 - 4 = 3
Menentukan Modus dengan rumusan

Mo = 33,7

Soal No.7

Diketahui data pada tabel berikut

Jika kuartil atasnya adalah 49,1. Tentukan nilai x

PEMBAHASAN :
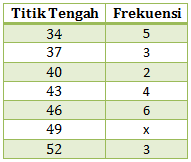
Karena titik tengah memiliki selisih = 3, maka panjang interval kelasnya (c) = 3. Kuartil atas berada pada titik tengah 49,1 berada pada interval 48-50.
Diketahui:
Q₃ = 49,1
tepi bawah (t_b) = 48,5
panjang interval kelas (c) = 3
banyaknya data (n) = 23 + x
Jumlah frekuensi sebelum kelas kuartil (Σ f_i) = 20
Untuk menentukan nilai x ditentukan dari rumusan kuartil atas:

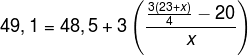
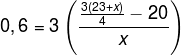
0,8x = 69 + 3x - 80
2,2x = 11
x = 5

Soal No.8

Jika diketahui data dengan rata-rata 42 dengan jangkauan 9. Jika data tersebut keduanya dikali x kemudian di tambah y maka dihasilkan rata-rata yang baru yaitu 85 dan jangkauan menjadi 19. Tentukan nilai 6x + y

PEMBAHASAN :
Diketahui:
Rata-rata awal = 42
jangkauan awal (J) = 9
Maka sesudah dikali x dan ditambah y maka nilainya menjadi

J = 9x + y = 19 ……pers (2)
Jika di eliminasi y, maka nilai x
33x = 66
x = 2
maka nilai y
9x + y = 19
9(2) + y = 19
18 + y = 19
y = 19 - 18 = 1
maka nilai 6x + y
6(2) + 1 = 13