Rangkuman Materi Pola & Barisan Bilangan Kelas 8 SMP

Pola Barisan Bilangan

Pola barisan bilangan adalah sebuah barisan bilangan yang penulisannya mengikuti pola-pola tertentu. Pola-pola tersebut yaitu:

Pola persegi

Pola persegi adalah pola bilangan yang dapat membentuk persegi atau sama dengan pola bilangan pangkat 2. Contohnya: 2, 4, 9, 16, … rumusnya: Un = n²

Pola persegi Panjang

Pola persegi Panjang adalah pola dari bilangan-bilangan yang dapat membentuk persegi Panjang. Contohnya: 2, 6, 12, 20, … rumusnya:

Un = n(n+1)

Pola segitiga

Pola barisan bilangan-bilangan yang dapat membentuk segitiga. Contohnya: 3, 6, 10, 15, … rumusnya:

Pola garis lurus

Pola bilangan garis lurus adalah penulisan bilangan dengan mengikuti pola garis lurus. Contohya:

mewakili bilangan 2

Pola

bilangan segitiga pascal

Pola bilangan segitiga pascal adalah pola dari jumlah bilangan pada baris-baris segitiga pascal. Contohnya: baris ke-4 atau U₄  terdiri atas bilangan 1, 2, 1. Barisan bilangannya adalah 1, 2, 4, 8, 16, … rumusnya:

U_n = 2^n-1

Pola bilangan ganjil

Pola bilangan ganjil adalah barisan bilangan yang pola bilangannya merupakan bilangan ganjil. Contohnya: 1, 3, 5, 7, 9, … rumusnya:

U_n = 2n-1

Pola bilangan genap

Pola bilangan genap adalah pola barisan yang bilangannya merupakan kumpulan bilangan genap. Contohnya: 2, 4, 6, 8, 10, 12, … rumusnya:

U_n = 2n

Barisan Bilangan

Barisan Aritmetika

Barisan aritmetika adalah barisan bilangan yang memiliki pola tetap menurut operasi penjumlahan dan pengurangan. Suku ke-n dari suatu bilangan dilambangkan dengan Un.

Contohnya:

Barisan aritmetika naik

2, 6, 10, 14, 18, … = 4 (beda positif)

Barisan aritmetika turun

20, 18, 16, 14, … = -2 (beda negatif)

Rumusnya:

suku ke-n barisan geometri:

U_n = a + (n-1)b

a = U₁ = suku pertama

b = beda

Barisan Geometri

Barisan geometri adalah barisan bilangan yang memiliki rasio tetap antara dua suku yang berurutan. Contohnya:

Barisan geometri naik (r > 1)

2, 4, 8, 16, 32, …

Barisan geometri turun (r < 1)

80, 40, 20, 10, …

Rumusnya:

Suku ke-n barisan geometri:

U_n = ar^n-1

a = U₁ = suku pertama

r = rasio

Deret Bilangan

Deret aritmetika

Deret aritmetika adalah penjumlahan dari suku-suku suatu barisan bilangan aritmetika.

Rumusnya:

S_n = jumlah suku deret aritmetika

a = U₁ = suku pertama

b = beda

Deret geometri

Deret geometri adalah penjumlahan dari suku-suku suatu barisan bilangan geometri.

Rumusnya:

a = U₁ = suku pertama

r = beda

Contoh Soal Pola & Barisan Bilangan Kelas 8 SMP

1. 17
2. 19
3. 20
4. 22

PEMBAHASAN :
Diketahui:
Suku pertama (a) = 4
beda (b) = 7-4 = 10-7 = 3
Ditanyakan suku ke 7 (U₇)
U₇ = a + (n-1)b = 4 + (7-1)3 = 22
Maka suku ke-7 adalah 22
Jawaban D

PEMBAHASAN :
Barisan tersebut memiliki pola barisan segitiga. Untuk menentukan suku ke-n pola barisan segitiga menggunakan rumusan:



Jawaban B

Diketahui barisan , x 2¹, x 2², x 2³…

PEMBAHASAN :
pola barisan , x 2¹, x 2², x 2³… dapat dituliskan menjadi

x 2⁰, x 2¹, x 2², x 2³. maka untuk suku ke n atau U_n = x 2^n-1
Jawaban D

PEMBAHASAN :
Menentukan banyaknya suku dapat kita peroleh dengan menentukan rumus barisanya, barisan 4, 7, 12, 19, …, 228. memiliki rumus barisan U_n = n² + 3, karena
4 → 12 +3
7 → 22 + 3
12 → 32 + 3
19 → 42 + 3
Maka untuk menentukan banyaknya suku bisa dilihat dari angka yang terbesar yaitu 228
228 = n² + 3
n² = 228 – 3 = 225
n = 15
Jawaban D

PEMBAHASAN :
Untuk menentukan U₈ maka kita harus mencari terlebih dahulu a (suku pertama) dan b (beda) nya dari U₃ dan U₆
U_n = a + (n-1)b
U₃ = a + 2b
41 = a + 2b
a = 41 – 2b…..(1)
U₆ = a + 5b
65 = a + 5b ….(2)
Substitusikan persamaan (1) ke persamaan (2) untuk menentukan nilai b
65 = (41-2b) +5b
65 = 41 + 3b
2b = 65 – 41 = 24
b = 8
Maka nilai a nya
65 = a + 5b = a + 5.8
65 = a + 40
a = 65 – 40 = 25
Menentukan nilai U₈
U₈ = a + 7b = 25 + 7.8 = 25 + 56 = 81
Jawaban C

1. 56.750
2. 78.125
3. 150.000
4. 156.250

PEMBAHASAN :
Untuk menentukan U₈ kita harus mengetahui rasio (r) dari barisan tersebut. Nilai a barisan tersebut = 2 dan r = 10/2 = 5, maka U₈ adalah
U_n = a. r^n-1
U₈ = 2. 5^8-1
U₈ = 156.250
Jawaban D

PEMBAHASAN :
Karena deret geometri maka berlaku:



8.2 = 18 – x
16 = 18 – x
x = 2
Jawaban D

PEMBAHASAN :
Karena deret geometri maka:
U₄ = ar³ = 2
U₈ = ar⁷ = 162
Maka jika dibandingkan:

r⁴ = 81
r = 3
Menentukan suku pertama dapat diambil dari U4
U₄ = ar³

Jawaban D

PEMBAHASAN :
Barisan bilangan ganjil tersebut adalah 1,3,5,7,….
U_n = (2n-1)
U₃₀ = 2.30 – 1 = 59
Karena termasuk deret aritmatika dengan a = 1, b = 3-1 = 2. Maka jumlah 30 bilangan ganjil adalah:


Jawaban C

Jumlah 5 suku pertama dari deret geometri  adalah …

PEMBAHASAN :
Dari soal dapat diketahui:
a =

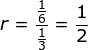
n = 5
Maka:


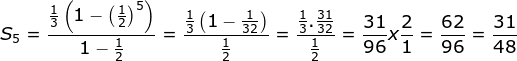
Jawaban A

1. 33, 39
2. 29, 33
3. 29,40
4. 24, 27

PEMBAHASAN :
Barisan dalam soal memiliki beda :
4 ke 5 bedanya 1
5 ke 8 bedanya 3
8 ke 13 bedanya 5
13 ke 20 bedanya 7
Maka dapat disimpulkan barisan tersebut memiliki beda bilangan ganjil sehingga dua suku berikutnya adalah 20 + 9 = 29 dan 29 + 11 = 40
Jawaban C

PEMBAHASAN :
Barisan tersebut membentuk barisan bilangan persegi panjang yang memiliki rumus:
n(n + 1), maka nilai U₉
U₉ = n(n + 1) = 9(9 + 1) = 9. 10 = 90
Jawaban C

PEMBAHASAN :
Bilangan segitiga Pascal memiliki pola sebagai berikut:

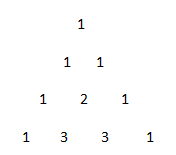
Menentukan jumlah bilangan pada baris ke n adalah 2^{n – 1}, maka jumlah bilangan pada baris ke 6 adalah
2^{6 – 1} = 2⁵ = 32
Jawaban B

PEMBAHASAN :
Barisan 46, 40, 34, 28, 22 termasuk ke dalam barisan deret aritmatika dengan a = 46 dan b = 40 – 46 = -6
maka rumus suku ke-n nya adalah
U_n = a + (n – 1)b = 46 + (n – 1)(-6) = 46 -6n + 6 = 52 – 6n
Jawaban A

PEMBAHASAN :
Diketahui:
a = -16
b = -10 – (-16) = 6
Jika suku ke-4 adalah x maka nilai x
U_n = a + (n – 1) b
U₄ = -16 + (4 – 1)6
x = -16 + 18 = 2
Jawaban C

PEMBAHASAN :
Jika kertas dibuat barisannya maka akan membentuk barisan
1, 2, 4, 8, 16,…
Barisan tersebut merupakan barisan geometri karena rasionya sama, yaitu

dengan a = 1
Maka jumlah potongan setelah suku kelima
U_n = ar^n-1
U_s = 1 x 2^5-1 = 2⁴ = 16 bagian
Jawaban B

PEMBAHASAN :
Diketahui:
a = 7
b = 10 – 7 = 3
Maka jumlah 15 suku pertamanya adalah

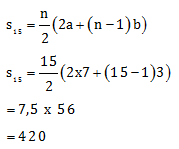
Jawaban D

PEMBAHASAN :
Suku ke-3
U₃ = a + 2b = 13
a = 13 – 2b … (i)

Suku ke-7
U₇ = a + 6b = 29 … (ii)
Persamaan (i) disubstitusikan ke (ii) menjadi:
(13 – 2b) + 6b = 29
⇒ 4b + 13 = 29
⇒ 4b = 16
⇒ b = 4
Maka a = 13 – 8 = 5

Menentukan n dari rumus jumlah deret

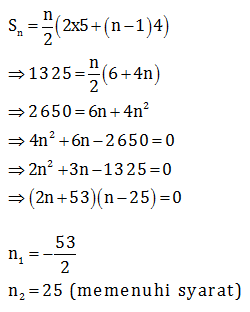
Maka, n = 25
Jawaban C

PEMBAHASAN :
Menentukan nilai a dari jumlah 7 suku pertama



Menentukan U₅
Un = ar^n-1
U₅ = 1. 3^5-1 = 1. 3⁴ = 81
Jawaban C

1. Rp. 3.000.000
2. Rp. 3.200.000
3. Rp. 3.500.000
4. Rp. 3.700.000

PEMBAHASAN :
Dari soal dapat diketahui:
a = 2.500.000
b = 300.000
n = 5
Maka gaji saat 5 tahun bekerja (U₅)
Un = a + (n-1) b
U₅ = Rp 2.500.000,00 + (5-1)Rp 300.000,00
= Rp 2.500.000,00 + Rp 1.200.000
= Rp 3.700.000,00
Jawaban D

1. 32 – 2n
2. 30 – 3n
3. 24 – 3n
4. 28 – 2n

PEMBAHASAN :
Barisan bilangan 21, 18, 15, 12, 9, … merupakan barisan deret aritmetika.
Diketahui:
a = 21
b = 18 – 21 = – 3

Maka untuk mencari rumus suku ke-n sebagai berikut:
U_n = a + (n – 1)b
= 21 + (n – 1)(- 3)
= 21 – 3n + 3
= 24 – 3n
Jawaban C

PEMBAHASAN :
-15, -10, -5, 0, 5, x, 15, 20
Diketahui:
a = – 15
b = -10 – (-15) = 5
x adalah suku ke-6

Maka nilai x dapat dihitung sebagai berikut:
U₆ = a + (n – 1)b
= -15 + (6-1)5
= -15 + 25
= 10
Jawaban A

PEMBAHASAN :
Berlaku jika b = U₂ – U₁ = U₃ – U₂
p – 3 = (3p + 2) – p
p – 3 = 2p + 2
p = – 5

Maka barisannya menjadi 3, -5, -13, …
a = 3
b = – 8
U_n = a + (n-1)b
U₅ = 3 + (5-1)-8
= 3 – 32
= – 29
Jawaban D

PEMBAHASAN :
Diketahui:

U₄ = 18

U₈ = 288

Untuk menghitung rasio adalah sebagai berikut:

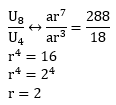
Jawaban B

PEMBAHASAN :
4, 16, 64, …
Diketahui:
a = 4
b = 16 – 4 = 12
n = 5
Menghitung rasio sebagai berikut:
a = U₁

Maka suku ke-n dapat dihitung sebagai berikut:
U_n = ar^n-1
U₅ = 4 x 4⁴
= 4 x 256
= 1024
Jawaban A