Contoh Soal & Pembahasan Pola & Barisan Bilangan SMP Bagian II

1. 33, 39
2. 29, 33
3. 29,40
4. 24, 27

PEMBAHASAN :
Barisan dalam soal memiliki beda :
4 ke 5 bedanya 1
5 ke 8 bedanya 3
8 ke 13 bedanya 5
13 ke 20 bedanya 7
Maka dapat disimpulkan barisan tersebut memiliki beda bilangan ganjil sehingga dua suku berikutnya adalah 20 + 9 = 29 dan 29 + 11 = 40
Jawaban C

DOWNLOAD CONTOH SOAL & PEMBAHASAN POLA & BARISAN SMP BAGIAN II DALAM BENTUK PDF KLIK DISINI

PEMBAHASAN :
Barisan tersebut membentuk barisan bilangan persegi panjang yang memiliki rumus:
n(n + 1), maka nilai U₉
U₉ = n(n + 1) = 9(9 + 1) = 9. 10 = 90
Jawaban C

PEMBAHASAN :
Bilangan segitiga Pascal memiliki pola sebagai berikut:

Menentukan jumlah bilangan pada baris ke n adalah 2^{n - 1}, maka jumlah bilangan pada baris ke 6 adalah
2^{6 – 1} = 2⁵ = 32
Jawaban B

PEMBAHASAN :
Barisan 46, 40, 34, 28, 22 termasuk ke dalam barisan deret aritmatika dengan a = 46 dan b = 40 - 46 = -6
maka rumus suku ke-n nya adalah
U_n = a + (n - 1)b = 46 + (n - 1)(-6) = 46 -6n + 6 = 52 - 6n
Jawaban A

PEMBAHASAN :
Diketahui:
a = -16
b = -10 - (-16) = 6
Jika suku ke-4 adalah x maka nilai x
U_n = a + (n - 1) b
U₄ = -16 + (4 - 1)6
x = -16 + 18 = 2
Jawaban C

PEMBAHASAN :
Jika kertas dibuat barisannya maka akan membentuk barisan
1, 2, 4, 8, 16,…
Barisan tersebut merupakan barisan geometri karena rasionya sama, yaitu

dengan a = 1
Maka jumlah potongan setelah suku kelima
U_n = ar^n-1
U_s = 1 x 2^5-1 = 2⁴ = 16 bagian
Jawaban B

PEMBAHASAN :
Diketahui:
a = 7
b = 10 - 7 = 3
Maka jumlah 15 suku pertamanya adalah

Jawaban D

PEMBAHASAN :
Suku ke-3
U₃ = a + 2b = 13
a = 13 – 2b … (i)

Suku ke-7
U₇ = a + 6b = 29 … (ii)
Persamaan (i) disubstitusikan ke (ii) menjadi:
(13 – 2b) + 6b = 29
⇒ 4b + 13 = 29
⇒ 4b = 16
⇒ b = 4
Maka a = 13 – 8 = 5

Menentukan n dari rumus jumlah deret

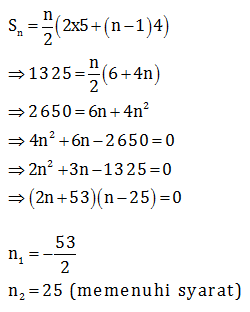
Maka, n = 25
Jawaban C

PEMBAHASAN :
Menentukan nilai a dari jumlah 7 suku pertama



Menentukan U₅
Un = ar^n-1
U₅ = 1. 3^5-1 = 1. 3⁴ = 81
Jawaban C

1. Rp. 3.000.000
2. Rp. 3.200.000
3. Rp. 3.500.000
4. Rp. 3.700.000

PEMBAHASAN :
Dari soal dapat diketahui:
a = 2.500.000
b = 300.000
n = 5
Maka gaji saat 5 tahun bekerja (U₅)
Un = a + (n-1) b
U₅ = Rp 2.500.000,00 + (5-1)Rp 300.000,00
= Rp 2.500.000,00 + Rp 1.200.000
= Rp 3.700.000,00
Jawaban D

DOWNLOAD CONTOH SOAL & PEMBAHASAN POLA & BARISAN SMP BAGIAN II DALAM BENTUK PDF KLIK DISINI