Rangkuman Materi Bab Lingkaran Kelas 8 SMP

Unsur-Unsur Lingkaran

1. Jari-jari lingkaran, adalah garis yang menghubungkan titik pusat lingkaran dengan titik pada keliling lingkaran. Contohnya garis OR, OQ, OP, dan OS.
2. Diameter lingkaran, adalah garis lurus antara dua titik pada keliling lingkaran yang melewati titik pusat lingkaran. Contohnya garis PQ dan garis RS.
3. Titik pusat lingkaran, adalah suatu titik yang berada tepat di tengah-tengah lingkaran. Contohnya titik O.
4. Busur lingkaran, adalah garis lengkung pada keliling lingkaran. Busur lingkaran di bagi 2 macam yaitu:
   • Busur kecil: panjangnya kurang dari setengah lingkaran
   • Busur besar: panjangnya lebih dari setengah lingkaran

   Contohnya: garis PR, RQ, QS, dan PS

5. Tali busur lingkaran, adalah garis lurus yang menghubungkan garis lengkung busur lingkaran pada keliling lingkaran tetapi tidak melewati titik pusat lingkaran. Contohnya garis lengkung PR, RQ, QS, dan PS.
6. Juring lingkaran, adalah daerah yang dibatasi atau diapit oleh dua garis jari-jari dan satu busur lingkaran. Juring lingkaran dibagi menjadi dua yaitu juring kecil dan juring besar tergantung besar kecilnya busur lingkaran. Contohnya daerah QOR.
7. Tembereng lingkaran, adalah daerah yang dibatasi oleh busur lingkaran dan tali busur lingkaran. Contohnya daerah busur PS dan tali busur PS.
8. Sudut lingkaran
   • Sudut pusat lingkaran: sudut antara dua buah jari-jari pada titik pusat lingkaran. Contohnya ∠POQ
   • Sudut keliling lingkaran: sudut yang terbentuk karena pertemuan antara dua tali busur dengan satu pada keliling lingkaran. Contohnya tali busur PR dan RQ bertemu di titik R sehingga membentuk ∠PRQ.

   Sifat-sifat sudut pada lingkaran, sebagai berikut:

   • Apabila sudut keliling suatu lingkaran menghadap diameter lingkaran, maka besar sudut keliling sama dengan 90⁰ .
   • Apabila sudut-sudut keliling menghadap busur yang sama, maka besar sudut-sudut keliling tersebut adalah sama.
   • Jumlah sudut keliling yang saling berhadapan adalah 180⁰ .
9. Garis singgung lingkaran, adalah garis yang memotong lingkaran tepat di satu titik pada keliling lingkaran. Contohnya perhatikan gambar di atas!
10. Apotema lingkaran, adalah garis tegak lurus dengan tali busur merupakan jarak terpendek antara tali busur dengan titik pusat lingkaran. Contohnya garis OU.

Rumus-Rumus Lingkaran

Luas lingkaran

L = π x r² atau L = ¼ π d² k

Keterangan:

π = phi = 3,14 = 22/7

r = jari-jari = ½ x d

d = diameter

Keliling lingkaran

K = 2 x π x r atau K = π x d

Garis singgung

Garis singgung melalui titik di luar lingkaran

Berlaku teorema Pythagoras:

Perhatikan ΔAOB!

OB² = OA² + AB²

Keterangan:

OA = r = jari-jari

OB = Jarak titik ke pusat lingkaran

AB = panjang garis singgung

Garis singgung dua lingkaran

1. Garis singgung persekutuan luar
   
   Berlaku teorema Pythagoras:
   Perhatikan ΔPQS!
   
   Keterangan:
   R = panjang jari-jari lingkaran besar
   r = panjang jari-jari lingkaran kecil
   k = jarak pusat lingkaran A dan B
   PS = R – r
   I = AB = panjang garis singgung lingkaran A dan B
2. Garis singgung persekutuan dalam
   
   Perhatikan ΔPQS!
   
   Keterangan:
   AB = d = panjang garis singgung persekutuan dalam
   R = panjang jari-jari lingkaran besar
   r = panjang jari-jari lingkaran kecil
   k = jarak titik pusat kedua lingkaran
   PS = jumlah jari-jari lingkaran P dan Q =  R + r

Lingkaran dalam dan lingkaran luar 

Jari-jari lingkaran luar segitiga:

Jari-jari lingkaran dalam segitiga:

Contoh Soal & Pembahasan Lingkaran Kelas 8 Tingkat SMP

1. 400,00 cm²
2. 454,323 cm²
3. 490,625 cm²
4. 521,425 cm²

PEMBAHASAN :
Diketahui
Keliling = 78,5 cm
Menentukan diameter dari keliling
K = π. d

Menentukan jari-jari dari diameter
d = 2. r
maka r = ½. d = ½. 25 cm = 12,5 cm
Maka luas lingkaran tersebut adalah
L = πr² = 3,14. (12,5)² = 490,625 cm²
Jawaban C

1. 28,26 cm²
2. 33,23 cm²
3. 38,56 cm²
4. 50,16 cm²

PEMBAHASAN :
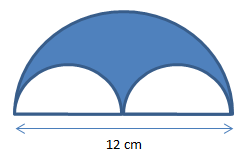
Menentukan luas daerah yang diarsir yaitu dengan mengurangkan luas setengah lingkaran besar dengan 2 luas setengah lingkaran kecil
Luas Arsir = luas setengah lingkaran besar – 2 x luas setengah lingkaran kecil
Menentukan luas setengah lingkaran besar
L = ½ . π. r² = ½ . 3,14. (½.12)² = ½ . 3,14. (6)² = 56,52 cm²
Menentukan luas setengah lingkaran kecil
L = ½ . π. r² = ½ . 3,14. (½.6)² = ½ . 3,14. (3)² = 14,13 cm²
Maka luas daerah yang di arsir adalah
L = 56,52 – 2. 14,13 = 56,52 – 28,26 = 28,26 cm²
Jawaban A

1. 50^o
2. 55,5^o
3. 60,5^o
4. 64,5^o

PEMBAHASAN :
Jika digambarkan sebagai berikut

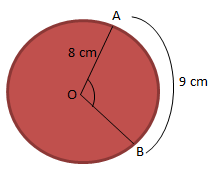
Menentukan ∠AOB dapat ditentukan dari perbandingan




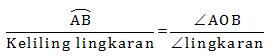
Jawaban D

1. 254,650^o
2. 289,56^o
3. 327,083^o
4. 376,54^o

PEMBAHASAN :
Jika digambarkan sebagai berikut

Menentukan ∠AOB



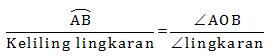
Menentukan luas juring AOB dengan menggunakan perbandingan




Jawaban C

1. 20,934 – 50√3 cm²
2. 34,654 – 50√3 cm²
3. 20,934 – 100√3 cm²
4. 34,654 – 100√3 cm²

PEMBAHASAN :
Menentukan luas juring AOB


Menentukan luas Δ AOB

tinggi segitiga diperoleh lewat phytagoras

maka luas Δ AOB
luas Δ AOB = ½. alat. tinggi = ½. 20. 10√3 = 100√3 cm²
Maka luas temberengnya
luas tembereng = luas juring – luas segitiga = 20,934 – 100√3 cm²
Jawaban C

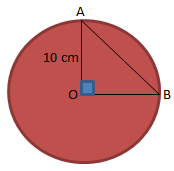
1. 8√2
2. 10√2
3. 12√2
4. 15√2

PEMBAHASAN :
Menentukan panjang tali busur abi bisa ditentukan menggunakan Phytagoras pada segitiga AOB

Jawaban B

1. 1 cm
2. 2 cm
3. 3 cm
4. 4 cm

PEMBAHASAN :
Diketahui
R = 12 cm
l = 6 cm
k = 10 cm
Menentukan jari-jari dihitung dari rumus persekutuan luar


Kuadratkan kedua sisi
36 = 100 – (144 – 24 r + r²
36 = 100 – 144 + 24r – r²
r² – 24r + 80 = 0
(r – 20) (r – 4) = 0
r = 20 atau r = 4 cm
jari-jari lingkaran B yang mungkin adalah 4 cm
Jawaban D

PEMBAHASAN :
Diketahui
R = 8 cm
r = 2 cm
k = 15 cm
Menentukan panjang garis singgung persekutuan dalam menggunakan rumus


Jawaban A

PEMBAHASAN 
Diketahui
d = 24 m, maka r = 12 m
Menentukan luas tanah yang akan ditanami rumput
L = luas taman – luas kolam
L = (π r²) – (pxl)
l = (3,14.(12)²) – 9 x 6 = 452,16 – 54 = 398,16 m²
Maka biaya pemasangannya adalah
Biaya = Luas yang akan ditanami x (harga rumput + harga pasang)
Biaya = 398,16 x (Rp. 6.000 + Rp. 4.000) = 398,16 x Rp. 10.000 = Rp. 3.981.600,00
Jawaban C

1. 197 cm²
2. 454,23 cm²
3. 867,34 cm²
4. 1480,24 cm²

PEMBAHASAN :
Diketahui:
panjang kertas = 60 cm
lebar kertas = 50 cm
d = 44 cm, maka r = 22 cm
Menentukan sisa kertas yang tidak terpakai
sisa = luas kertas – luas lingkaran
sisa = (p x l) – (πr²)
sisa = (60 x 50) – (3,14. (22)²) = 3000 – 1519,76
sisa = 1480,24 cm²
Jawaban D

1. Tembereng
2. Juring
3. Segitiga
4. Tali busur

PEMBAHASAN :
Pada unsur-unsur lingkaran yang dimaksud dengan juring adalah daerah yang dibatasi atau diapit oleh dua garis jari-jari dan satu busur lingkaran. Sedangkan tembereng adalah daerah yang dibatasi oleh busur lingkaran dan tali busur lingkaran.
Jawaban B

1. 80,32
2. 78,55
3. 75,36
4. 72,31

PEMBAHASAN :
Diketahui:
r = 12 cm
π = 3,14

Menghitung panjang keliling lingkaran adalah sebagai berikut:
K = 2πr = 2 x 3,14 x 12 cm = 75,36 cm
Jawaban C

1. 41,12
2. 39,5
3. 35,09
4. 30,87

PEMBAHASAN :
Diketahui:
d = 16 m

Menentukan panjang batas kolam yang dipasangi keramik adalah sebagai berikut:

panjang batas kolam = ½ keliling lingkaran + diameter
.                                      = (½ x π x d) + d = (½ x 3,14 x 16 m) + 16 m = 41,12 m
Jawaban A

1. 10
2. 11
3. 12
4. 13

PEMBAHASAN :
Diketahui:
L = 132,665 cm²
Maka, panjang jari-jari dapat dihitung sebagai berikut:
L = ¼ x L lingkaran
132,665 = ¼ x 3,14 x r²
132,665 = 0,785 x r²
r² = 169
r = 13
Jawaban D

1. 356,78
2. 452,42
3. 510,25
4. 555,13

PEMBAHASAN :
Diketahui:
Diameter lingkaran besar (d) = 30 cm atau r = ½ x 30 cm = 15 cm
Dameter lingkaran kecil (d) = 20 atau r = ½ x 20 cm = 10 cm

Maka, luas daerah yang diarsir dapat dihitung sebagai berikut:
Luas = Luas setengah lingkaran besar + luas setengah lingkaran kecil
.         = (½ x π x r²) + (½ x π x r²) = (½ x 3,14 x (15)²) + (½ x 3,14 x (10)²)
.         = 353,25 + 157 = 510,25
Jawaban C

1. 452,42
2. 510,25
3. 555,13

PEMBAHASAN :
Diketahui:
Diameter lingkaran (d) = 50 m
panjang satu lintasan lurus = 100 m

Menghitung panjang lintasan sebagai berikut:
Panjang lintasan atau keliling = (2 x panjang lintasan lurus) + (keliling lingkaran)
.                                                      = (2 x 100 m) + (3,14 x 50 m) = 200 m + 157 m = 357 m
Jawaban A

1. 452,42
2. 510,25
3. 555,13

PEMBAHASAN :
Diketahui:
Diameter lingkaran (d) = 50 m
panjang satu lintasan lurus = 100 m

Menghitung panjang lintasan sebagai berikut:
Panjang lintasan atau keliling = (2 x panjang lintasan lurus) + (keliling lingkaran)
.                                                      = (2 x 100 m) + (3,14 x 50 m) = 200 m + 157 m = 357 m
Jawaban A

1. 23,13 cm
2. 32,15 cm
3. 39,25 cm
4. 40,15 cm

PEMBAHASAN :

Diketahui:
OP = r = 15 cm
Titik pusat = titik O
∠POQ = 150⁰

Dengan perbandingan, dapat dihitung panjang busur PQ sebagai berikut:

Jawaban C

1. 200,5
2. 209,3
3. 214,5
4. 287,2

PEMBAHASAN :

Diketahui:
OA = 20 cm
∠AOB = 60⁰

Maka luas juring POQ dapat dihitung sebagai berikut:

Jawaban C

1. 11,2
2. 12,3
3. 13,2
4. 14,5

PEMBAHASAN :

Diketahui:
luas juring POQ = 45,6 cm²
∠POQ = 42⁰

Mencari luas lingkaran dapat dihitung sebagai berikut:

Untuk menghitung jari-jari lingkaran dapat dihitung sebagai berikut:

Menentukan jari-jari dari luas lingkaran
L = πr²
391 = 3,14 x r²
r² = = 125
r   = = 11,2 cm
Jawaban A

1. 50⁰
2. 65⁰
3. 70⁰
4. 75⁰

PEMBAHASAN :
Diketahui:
∠POB = 130⁰

Pada lingkaran luar segitiga seperti gambar diatas berlaku:
∠PRQ = ½ x ∠POQ = ½ x 130⁰ = 65⁰
Jawaban B

1. 20⁰
2. 30⁰
3. 40⁰
4. 50⁰

PEMBAHASAN :
Diketahui:
∠A = 5x
∠B = 90⁰
∠C = 4x
∠ABC = 180⁰

Menentukan nilai ∠C
∠A + ∠B + ∠C = 180⁰
5x   +  90⁰ + 4x = 180⁰
.                       9x = 90⁰
.                          x = 10⁰
maka, ∠ACB = ∠C = 4x = 4 x 10⁰ = 40⁰
Jawaban C

1. Sudut keliling harus bertolak belakang dengan sudut pusat
2. Sudut keliling suatu lingkaran yang menghadap diameter lingkaran, maka besar sudut keliling sama dengan 90⁰ .
3. Sudut-sudut keliling yang menghadap busur yang sama, maka besar sudut-sudut keliling tersebut akan sama.
4. Jumlah sudut keliling yang saling berhadapan adalah 180⁰ .

PEMBAHASAN :
Sifat-sifat sudut keliling adalah:

• Apabila sudut keliling suatu lingkaran menghadap diameter lingkaran, maka besar sudut keliling sama dengan 90⁰ .
• Apabila sudut-sudut keliling menghadap busur yang sama, maka besar sudut-sudut keliling tersebut adalah sama.
• Jumlah sudut keliling yang saling berhadapan adalah 180⁰ .

Jawaban A

1. Tali busur
2. Apotema
3. Tembereng
4. Busur

PEMBAHASAN :

• Tali busur: garis lurus yang menghubungkan garis lengkung busur lingkaran pada keliling lingkaran tetapi tidak melewati titik pusat lingkaran.
• Apotema: garis tegak lurus dengan tali busur merupakan jarak terpendek antara tali busur dengan titik pusat lingkaran.
• Tembereng: daerah yang dibatasi oleh busur lingkaran dan tali busur lingkaran.
• Busur: garis lengkung pada keliling lingkaran.

Jawaban C

1. 698,6
2. 706,5
3. 728,2
4. 755,6

PEMBAHASAN :
Diketahui:
K = 94,2 cm
π = 3,14

Menentukan panjang jari-jari lingkaran dapat dihitung sebagai berikut:
K = 2πr
94,2 = 2 x 3,14 x r
94,2 = 6,28 x r
r  = 15 cm

Maka, luas lingkaran dapat dihitung sebagai berikut:
L = πr² = 3,14 x 15² = 706,5 cm²
Jawaban B

1. 4 : 1
2. 3 : 1
3. 2 : 1
4. 1 : 1

PEMBAHASAN :
Diketahui:
r_p = 2 x r_Q

Maka untuk menghitung besar perbandingan luas lingkaran P dan Q adalah:

Maka perbandingannya adalah 4 : 1
Jawaban A

1. 50⁰
2. 60⁰
3. 70⁰
4. 80⁰

PEMBAHASAN :
Diketahui:
∠POQ = 120⁰

Pada lingkaran luar segitiga seperti gambar diatas berlaku:
∠PTQ = ½ x ∠POQ = ½ x 120⁰ = 60⁰
Jawaban B

1. 1
2. 2
3. 3
4. 4

PEMBAHASAN :
Garis singgung lingkaran  adalah garis yang memotong lingkaran tepat di satu titik pada keliling lingkaran.
Jawaban A

1. 9 cm
2. 10 cm
3. 11 cm
4. 12 cm

PEMBAHASAN :
Diketahui:
R = 7 cm
r = 5 cm
k = 15 cm

maka panjang garis singgung persekutuan dalam (d) dapat dihitung sebagai berikut:

Jawaban A

1. 10,5
2. 11
3. 12,5
4. 13

PEMBAHASAN :
Diketahui:
Panjang sisi a = 15 cm
Panjang sisi b = 20 cm
Panjang sisi c = 25 cm

Menentukan luas segitiga sebagai berikut:
L = ½ x 15 cm x 20 cm
.  = 150 cm²

Menentukan jari-jari lingkaran luar segitiga adalah:

Jawaban C

1. 2,9
2. 4,5
3. 5
4. 5,4

PEMBAHASAN :
Diketahui:
Panjang sisi a = 15 cm
Panjang sisi b = 20 cm
Panjang sisi c = 25 cm

Menentukan luas segitiga sebagai berikut:
L = ½ x 15 cm x 20 cm
.  = 150 cm²

Menentukan panjang jari-jari lingkaran dalamnya sebagai berikut:
s = ½ x keliling segitiga
.  =  ½  x (15 cm +20 cm + 25 cm)
.  = 30 cm

Maka jari-jari lingkaran dalamnya adalah

Jawaban C

1. 95⁰
2. 90⁰
3. 205⁰
4. 105⁰

PEMBAHASAN :
Diketahui:
∠juring kecil POQ = 150⁰
∠juring besar POQ = 360⁰ – 150⁰ = 210⁰

Maka besar ∠PRQ = ½ x 210⁰ = 105⁰
Jawaban D

1. 31,1
2. 26,8
3. 33,9
4. 41,2

PEMBAHASAN :
Diketahui:
R = 12 cm
r = 6 cm
k = 36 cm

Untuk menghitung panjang garis singgung persekutuan dalam (d) adalah:

Jawaban A

1. 31,1
2. 26,8
3. 33,9
4. 41,2

PEMBAHASAN :
Diketahui:
R = 12 cm
r = 6 cm
k = 36 cm

Untuk menghitung panjang garis singgung persekutuan dalam (d) adalah:

Jawaban A

1. 43
2. 45
3. 37
4. 39

PEMBAHASAN :
Diketahui:
R = 10 cm
r  = 6 cm
d = 42 cm

Rumus yang berlaku untuk garis singgung persekutuan dalam untuk menentukan jarak antara titik pusat Pdan Q sebagai berikut:

Jawaban B

1. 43
2. 45
3. 37
4. 39

PEMBAHASAN :
Diketahui:
Jari-jari lingkaran besar = r_b = 8 cm + 4 cm = 12 cm
Jari-jari lingkaran kecil = r_k = 8 cm

Maka untuk menghitung luas daerah yang diarsir sebagai berikut:
Luas daerah yang diarsir = ½ luas lingkaran besar – ½ luas lingkaran kecil

Jawaban D

1. 75,76
2. 77,68
3. 81,12
4. 85,32

PEMBAHASAN :
Menentukan keliling setengah lingkaran
K = ½  x (π x d)
K  = ½  x (3,14 x 12 cm) = 18,84 cm

Menentukan keliling persegi panjang
K = 2 x (p + l)
K= 2 x (12 cm + 8 cm) = 40 cm

Menentukan keliling seperempat dua lingkaran
K = 2 x (1/4 x π x d)
K = 2 x (1/4 x 3,14 x 12 cm) = 18,84 cm

Maka besar keliling gambar yang diarsir adalah 18,84 cm + 40 cm + 18,84 cm = 77,68 cm
Jawaban B

1. 178,12
2. 180,43
3. 197,36
4. 209,04

PEMBAHASAN :
Menentukan luas setengah lingkaran
L = ½  x (π x r²)
L = ½  x (3,14 x 6² cm) = 56,52 cm

Menentukan luas persegi panjang
L = p x l = 12 cm x 8 cm = 96 cm²

Menentukan luas seperempat lingkaran
L = 2 x (1/4 x π x r²)
L = 2 x (1/4 x 3,14 x 6² cm) = 56,52 cm

Maka besar keliling gambar yang diarsir adalah 56,52 cm + 96 cm + 18,84 cm = 209,04 cm
Jawaban D

1. 28,2
2. 31,4
3. 37,5
4. 40,3

PEMBAHASAN :
Diketahui:
OP = OQ = 30 cm
∠POQ = 60⁰

Maka, untuk menghitung panjang busur PQ adalah sebagai berikut:

Jawaban D

1. 13,4
2. 14
3. 14,9
4. 15

PEMBAHASAN :
Diketahui:
OQ = 6 cm
PQ = 12 cm
∠PQO = sudut siku-siku

Maka untuk menghitung panjang OP berlaku sebagai berikut:

Jawaban A

1. 400
2. 300
3. 200
4. 100

PEMBAHASAN :
Diketahui:
∠ABO = sudut siku-siku
AB = 18 cm
OA = 24 cm

Menentukan jari-jari lingkaran sebagai berikut:

Maka keliling lingkaran dapat dihitung sebagai berikut:
K = 2πr
K = 2 x 3,14 x 15,9 cm = 100 cm
Jawaban D