Contoh Soal Bilangan Berpangkat dan Bentuk Akar Kelas 9 SMP
Soal No.31
Bentuk pecahan dari 
adalah …
adalah …
PEMBAHASAN :
Jawaban C
Soal No.32
Hasil perhitungan dari 
- 0,01
- 0,02
- 0,03
- 0,04
PEMBAHASAN :
Jawaban C
Soal No.33
Hasil perhitungan dari 
PEMBAHASAN :
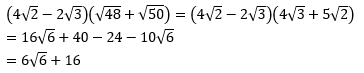
Jawaban A
Soal No.34
Sebuah persegi panjang memiliki panjang 
cm dan lebar 
cm. Maka luas persegi panjang tersebut adalah …
cm dan lebar 
cm. Maka luas persegi panjang tersebut adalah …
PEMBAHASAN :
Jawaban D
Soal No.35
Diketahui 
maka nilai a adalah …
maka nilai a adalah …- -5
- -7
- -9
- -11
PEMBAHASAN :
Jawaban C
Soal No.36
Diketahui sebuah bangun persegi memiliki panjang diagonal 36 cm. Maka luas persegi adalah …
- 256 cm2
- 648 cm2
- 560 cm2
- 480 cm2
PEMBAHASAN :
Jawaban B
Soal No.37
Sebuah segitiga dengan panjang alas 
dan tinggi 
. Maka luas segitiga tersebut adalah …
dan tinggi 
. Maka luas segitiga tersebut adalah …
PEMBAHASAN :
Jawaban D
Soal No.38
Hasil perhitungan dari 
- 4
- 6
- 9
- 12
PEMBAHASAN :
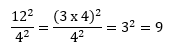
Jawaban C
Soal No.39
- 2x + 4y
- 3x – 4y
- 2x + 5y
- -4x – 3y
PEMBAHASAN :
Jawaban A
Soal No.40
Jika 
maka nilai x = …
maka nilai x = …- 4
- 6
- 8
- 10
PEMBAHASAN :
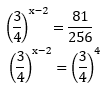
Maka nilai x:
x – 2 = 4
x = 6
Jawaban B
Sangat membantu sekali buat belajar adik saya.
Sangat membantu dan mudah di mengerti
Alhamdulillah terima kasih untuk latihan dan pembahasan soal-soal ini. Sangat membantu dan bermanfaat dalam proses belajar saya