Kumpulan Soal Ulangan Barisan, Deret dan Notasi Sigma Beserta Pembahasannya

Kumpulan Soal Ulangan Barisan, Deret dan Notasi Sigma Dengan Pembahasannya

Soal No.1
Diketahui suku kedua suatu deret aritmatika adalah 5. Jika dijumlahkan suku keempat dan suku keenam hasilnya 28. Tentukan suku kesembilan dari deret aritmatika tersebut.

PEMBAHASAN :
Diketahui U2 = 5, maka a + b = 5
U4 + U6 = 28
Menentukan beda
U4 + U6 = 28
(a+3b) + (a+5b) = 28 (mengubah ke bentuk a +b)
(a+b + 2b) + (a+b+4b) = 28
(5+2b) + (5+4b) = 28
10 + 6b = 28
6b = 18
b = 3
Menentukan a
Substitusikan b ke a+b = 5
a + 3 = 5
a = 2
Menentukan U9
U9 = a + 8b
U9 = 2 + 8.3 = 2 + 24 = 26

Soal No.2
Dalam perlombaan mengambil kelereng. 8 kelereng diletakan pada garis lurus diketahui dua kelereng yang berdekatan memiliki jarak 6 meter. Jika jarak kelereng pertama ke garis pengambilan berjarak 6 meter. Tentukan jarak total anak yang mengambil 8 kelereng bolak balik mengambil satu kelereng ke garis pengambilan dengan satu pengambilan.

PEMBAHASAN :
Diketahui
b = 6 meter
Jarak total dapat dihitung dari deret aritmatika x 2 karena bolak balik
dengan a = 0 meter dan n = 9 karena kelereng pertama merupakan suku ke 2, maka


Karena bolak balik, maka jarak total yang ditempuh adalah 2x nya
Jarak total = 2 x 216 m = 432 m

Soal No.3
Diketahui barisan 1,3,9,27
Tentukanlah:
a. rumus suku ke-n
b. suku ke-9

PEMBAHASAN :
Dari barisan tersebut dapat diketahui nilai rasionya

  1. menentukan rumus suku ke n
    Un = a.rn-1
    Un = 1.3n-1Un= 3n-1
  2. Menentukan suku ke-9
    U9 = 3n-1 = 39-1 = 38 = 6561
Soal No.4
Jika diketahui tiga bilangan rasional membentuk barisan aritmatika. Jumlah ketiga bilangan 42 dan hasil kalinya 2.520. Tentukan bilangan terkecilnya

PEMBAHASAN :
Misalkan tiga bilangan rasional itu : x,y,z
maka a = x, b = y-x


42 = 3y
y = 14
U1.U2.U3 =2.520
x.(x+(y-x)).(x+2(y-x))=2.520
(x2+xy-x2)(x+2y-2x) = 2.520
xy(2y-x) = 2.520
14x(28-x) = 2.520
392x – 14x2 = 2.520
14x2-392x+2.520 = 0
x2 – 28x + 180 = 0
(x – 18) (x-10) =0
x1 = 18 atau x2 = 10
maka angka ketiga bilangan tersebut adalah : 10, 14, 18
dan yang terkecil adalah 10

Soal No.5
Tentukan bentuk notasi sigma dari deret berikut:

PEMBAHASAN :
notasi sigma deret tersebut adalah

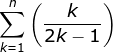
k = 1 merupakan batas bawah, sedangkan n disebut batas atas. penjumlahan yang ditulis dalam notasi sigma ini merupakan penjumlahan  pertama

Soal No.6
Nyatakanlah bentuk notasi sigma berikut dalam bentuk deret!

PEMBAHASAN :
notasi sigma di atas memiliki batas atas = 5 dan batas bawah n = 5, maka penjumlahan 10 bilangan pertama yaitu

Soal No.7
Sebuah bola dijatuhkan dari ketinggian 1 meter. Setiap kali sesudah jatuh mengenai lantai, bola itu dipantulkan lagi dan mencapai tinggi  dari tinggi sebelumnya. Tentukanlah panjang seluruh jalan yang dilalui bola itu sampai berhenti!

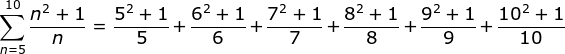
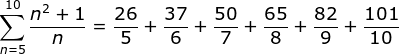
PEMBAHASAN :
diketahui:
Untuk sekali pantul panjangnya : (1 + 3/4)m = 7/4 m
rasio (r) nya = 3/4
Karena -1<r<1 dimana rn menuju 0 sehingga menentukan panjang lintasannya menggunakan deret geometri tak terhingga
maka:

Soal No.8
Diketahui barisan sepuluh bilangan a1, a2, a3,…., a10 Jika a1 = 2p+25, a2 = -p + 9, a3 = 3p + 7, dan an+1 – an untuk n = 1, 2, 3, ….., 9 tentukan jumlah semua bilangan tersebut

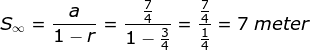
PEMBAHASAN :
Barisan tersebut termasuk barisan aritmatika, sehingga:
a2 – a1 = a3 – a2
(-p + 9) – (2p + 25) = (3p +7) – (-p+9)
-p + 9 – 2p – 25 = 3p + 7 + p – 9
-3p – 16 = 4p -2
-7p = 14
p = -2
Menentukan beda (b)
a1 = 2p + 25 = 2.(-2) + 25 = 21
a2 = -p + 9 = -(-2) + 9 = 11
maka b = a2 – a1 = 11 – 21 = -10
Maka jumlah bilangan tersebut

Soal No.9
Tentukan nilai x agar deret geometri berikut konvergen
(x-2) + (x-2)2 + (x-2)3 + ….

PEMBAHASAN :
Menentukan rasio (r)

Agar deret geometri tersebut konvergen,
haruslah -1 < r < 1 sehingga:
-1 < x-2 < 1.
x-2 < 1
(x-2)2 < 12
x2 – 2x + 2 < 1
x – 2)2 – 12 < 0
(x – 2 + 1)(x – 2 – 1) < 0
(x – 1)(x – 3) < 0
x = 1 dan x = 3
maka  1 < x < 3

Soal No.10
Suku pertama suatu deret geometri adalah x-4, suku ke-3 adalah x2a, dan suku ke-8 adalah x52. Tentukanlah nilai a dan jumlah 10 suku pertama deret tersebut!

PEMBAHASAN :
Diketahui :
U1 = x-4
U3 = ar2 = x2a
U8 = ar7 = x52
Menentukan rasio (r)
U3 = x-4.r2 = x2a

   ……..(1)
U3 – U2 = U2 – U1
x2.6 – U2 = U2 – x-4
2U2 = x12 + x-4 = x8
U2 = 1/2 x8
  ……..(2)
Substitusikan pers (1) dan (2)
xa+2 = 1/2 x12
x8 = 1/2 x12
1/2 = x-4
x = 1,189
r = x8 = (1,189)8= 4
Menentukan nilai a
U8 = ar7 = x52 =x-4 . x7(a+2) = x-4+7a+14 = x10+7a
52 = 10 + 7a
7a = 42
a = 6
Menentukan jumlah suku pertama
a = U1 = x-4 = (1,189)-4 = 0,5

Soal No.11
Jumlah deret tak hingga deret 1

PEMBAHASAN :
Diketahui :
deret 1
Maka: a = 1 dan deret 2
Jumlah deret tak hingga dapat dihitung sebagai berikut:
deret 3
deret 8
deret 5
deret 6
deret 7

Soal No.12
Tentukan jumlah deret geometri tak hingga deret 9 = …

PEMBAHASAN :
Diketahui :
deret 9
a = 10
deret 10
Berlaku rumus:
deret 3
Maka jumlah deret tak hingga dapat dihitung sebagai berikut:
deret 11
deret 12
= 30

Soal No.13
Tentukan suku ke-n dari deret hitung 2,6,10,14, … jika jumlah n suku pertama adalah 288!

PEMBAHASAN :
Diketahui :
Barisan bilangan 2,6,10,14, …
a = 2
b = 4
Jumlah n suku pertama = 288
Berlaku rumus:
deret 13
Menentukan banyaknya suku sebagai berikut:
deret 15
288= n (2 + (n – 1) 2)
288 = n (2 + 2n – 2)
288 = deret 16
144 = deret 17
n = 12
Maka suku ke-12 dapat dihitung sebagai berikut:
U12 = a + (n – 1) b
= 2 + 11 . 4
= 46

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.

You cannot copy content of this page