Rangkuman, Contoh Soal & Pembahasan Getaran

Rangkuman Getaran & Gerak Harmonik

PENGERTIAN GETARAN

Getaran merupakan gerakan bolak-balik secara periodik melalui titik kesetimbangan.

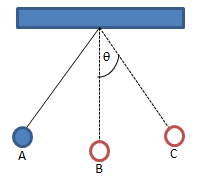
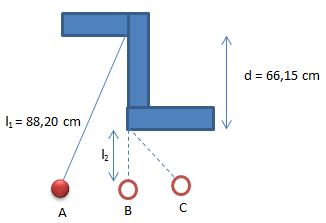
Getaran pada ayunan sederhana

get3

A dan C disebut titik tertinggi sedangkan B disebut titik kesetimbangan. Satu getaran terjadi saat bandul melintas mulai dari A dan kembali lagi ke A. Jadi satu getaran itu dari A – B – C – B – A. Satu getaran lengkap adalah gerakan bolak-balik dari A ke C dan kembali lagi ke A. Waktu yang dibutuhkan untuk melakukan satu getaran lengkap disebut periode. Sedangkan banyaknya getaran atau gerak bolak-balik yang dapat dilakukan dalam waktu satu detik disebut frekuensi. Hubungan periode (T) dan frekuensi (f) dinyatakan oleh:

get4

Gaya pemulih, periode dan frekuensi ayunan sederhana

get1
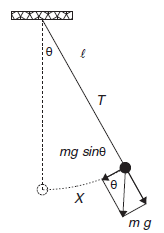
Gaya pemulih merupakan gaya yang menyebabkan benda kembali ke keadaan semula. Dirumuskan sebagai berikut:
F = – k.x atau
F = -m.g.sin θ atau
GET5
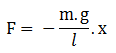
Keterangan:
F : gaya (N)
k : tetapan gaya
m : massa benda (kg)
g : percepatan gravitasi (m/s2)
θ : sudut simpangan
l : panjang tali (m)
x : simpangan getar (m)

Tanda minus (-) menunjukkan bahwa arah gaya F berlawanan dengan arah simpangan.

Periode getaran pada ayunan sederhana
Dirumuskan sebagai berikut:
get6
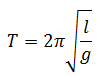
Frekuensi getaran pada ayunan sederhana
Dirumuskan sebagai berikut:
get7
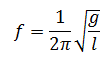
T : periode getaran (s)
g : percepatan gravitasi (ms-2)
π : 3.14 = 22/7
l : panjang tali (m)
f : frekuensi getaran (Hz)

Getaran pada pegas

Gaya pemulih, periode dan frekuensi pada pegas
get8
Gaya pemulih pada pegas dirumuskan sebagai berikut:
F = – k.∆x
Keterangan:
F : gaya yang bekerja pada pegas (N)
k : konstanta pegas (N/m)
∆x : pertambahan panjang pegas (m)
Periode Getaran Pada Pegas
Dirumuskan sebagai berikut:
get9
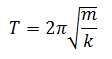
Frekuensi getaran pada ayunan sederhana
Dirumuskan sebagai berikut:
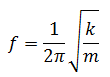
get10
T = periode getaran (s)
π = 3.14 = 22/7
k = tetapan pegas (Nm-1)
f = frekuensi getaran (Hz)
m = massa beban (kg)
Nilai konstanta suatu pegas dapat ditentukan dari persamaan:
k = m.ω2
Keterangan
ω : kecepatan sudut dari gerak pegas (rad/s)
Jika disusun seri maka menentukan k dengan persamaan:
get11
Jika disusun paralel maka menentukan k dengan persamaan:
kparalel = k1 + k2 + k3 + ………..

Persamaan Simpangan, Kecepatan, dan Percepatan

Jika benda melakukan gerak harmonik sederhana dengan sudut awal θo maka persamaan simpangannya

y = A sin(ωt + θ0)
Keterangan:
y = Simpangan (meter)
A = Amplitudo (meter)
θ0 = Frekuensi (rad/s)
ω = Sudut fase awal (rad)
t = waktu titik tersebut telah bergetar (s)

Persamaan kecepatan getaran harmonik adalah:

v = Aωcos(ῴt + θ0)
persamaan dari percepatan gerak harmonik dinyatakan sebagai:
a = -Aω2 sin(ωt + θ0)

Sudut Fase, Fase, dan Beda Fase

Sudut fase dapat dituliskan sebagai berikut:
θ =(ῴt + θ0)
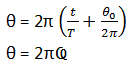
get12
Keterangan:
Ҩ = fase.
Beda fase yang dihasilkan diantara dua kedudukan adalah
ΔҨ = Ҩ2 – Ҩ1
get13

hukum kekekalan energi mekanik pada getaran harmonik

Semua benda yang bergerak mempunyai energi kinetik dan energi potensial. Benda yang bergerak harmonik sederhana juga mempunyai energi kinetik dan energi potensial.

Energi potensial

di rumuskan sebagai berikut
EP = ½ ky2
EP = ½ mω2 A2 sin2ωt
Keterangan
Ep = energi potensial (joule)
m = massa benda (kg)
A = amplitudo (m)
ω = kecepatan sudut(rad/s)
t = waktu (sekon)

Energi kinetik

di rumuskan sebagai berikut
Ek = ½ mv2
Ek = ½ mω2A2cos2ωt
Ek = ½ k (A2-y2)

Energi mekanik

Energi mekanik merupakan jumlah energi potensial dan energi kinetik.
EM = Ep + Ek = ½kA2.

superposisi getaran

Benda dapat mengalami dua getaran sekaligus. Jika suatu benda melakukan dua getaran sekaligus akan membentuk gelombang getaran yang di peroleh dengan menjumlahkan simpangan tiap-tiap getaran.

Contoh Soal & Pembahasan Getaran & Gerak Harmonik

Informasi berikut digunakan untuk menjawab soal no 1 dan 2
Sebuah beban bermassa m yang diikatkan pada ujung kanan sebuah pegas dengan konstanta pegas k diletakkan pada lantai datar dengan ujung pegas sebelah kiri terikat pada dinding. Beban ditarik ke kanan sampai ke titik A yang berjarak a dari titik setimbang dan kemudian dilepaskan sehingga berosilasi.
Soal No.1 (UTBK 2019)
Setelah dilepas, beban bergerak ke kiri melewati titik setimbang O dan berhenti sesaat pada jarak b di sebelah kiri titik setimbang. Kemudian, beban bergerak ke kanan dan berhenti sesaat pada jarak c di sebelah kanan titik setimbang. Apabila Ek adalah energi kinetik sistem dan Ek di O sama dengan ½ kb2, maka…
  1. b < c
  2. b > c
  3. b < a
  4. b = a
  5. b > a

PEMBAHASAN :

  • Energi potensial
    EP = ½ ky2
    Dengan
    m = massa benda
    A = amplitudo
    Y = simpangan
  • Energi Kinetik
    EK = ½ mv2
    Atau
    EK = ½ k (A2 – y2)
    Dengan
    m = massa benda
    A = amplitudo
    v = kecepatan
    Y = simpangan
    K = konstanta
  • Energi Mekanik
    Energi mekanik adalah jumlah energi potensial dengan energi kinetik
    EM = EP + EK
    EM = ½ kA
  • Situasi energi potensial, kinetik dan Mekanik pada titik setimbang dan Terjauh
    1. Pada titik setimbang (y = 0)
      • Kecepatan bernilai maksimum (vmak), akibatnya EK maksimum
        Energi Mekanik = EKMAKSIMUM = ½ mvmaks2 = ½ kA2
      • Percepatan nol
      • Energi potensial nol (y = 0)
    2. Pada titik terjauh (y = A)
      • Simpangan maksimum (ymaksimum) akibatnya EPmaksimum
      • Energi Mekanik = EPMAKSIMUM = ½ kymaks2 = ½ kA2
      • Kecepatan nol
      • Percepatan maksimum akibatnya gaya pulih maksimum

Pernyataan diatas: “…. beban bergerak ke kiri melewati titik setimbang O dan berhenti sesaat pada jarak b kemudian bergerak ke kanan..”
Artinya: titik b merupakan titik terjauh (amplitudo), energi mekanik di titik ini adalah
EM = ½ Kymaks2
EM = ½ kb2
Pernyataan diatas: “….beban bergerak ke kanan dan berhenti sesaat pada jarak c sebelah kanan titik setimbang..”
Artinya: titik c merupakan titik terjauh (amplitudo) juga
Pernyataan diatas: “…. beban di tarik ke kanan sampai ke titik A yang berjarak a dari titik setimbang..”
Artinya titik a merupakan titik terjauh (amplitudo) juga
Kesimpulan a = b = c
Jawaban D

Soal No.2 (UTBK 2019)
Setelah dilepas, beban bergerak ke kiri melewati titik setimbang dan berhenti sesaat di titik B, pada jarak b di sebelah kiri titik setimbang. Andaikan lantai kasar dan sampai di titik setimbang energi mekanik berkurang sebesar ε, usaha gaya gesek dari titik A sampai titik B adalah…

PEMBAHASAN :
Gaya gesek merupakan termasuk gaya non konservatif, untuk itu berlaku:
WTotal = Wkonservatif + Wnon konservatif
ΔEk = – ΔEp + Wnon konservatif
Wnon konservatif = ΔEk+ΔEp
Wnon konservatif = ΔEm
Pada situasi soal di atas, dari posisi A ke posisi setimbang O timbul gaya gaya gesek, usaha gaya gesek dari A ke O adalah
Wf = -Fg s
Wf = -Fg a
Jika ditinjau dari energi mekanik, energi mekanik dari posisi A ke posisi O berkurang sebesar ε dengan demikian: (Gaya gesek merupakan termasuk gaya non konservatif)
ε = -Fg a
                        (1)
Untuk situasi dari posisi A ke B, usaha yang dilakukan gaya gesek adalah:
WFAB = WFA + WFB
WFAB = -Fg a -Fg b
WFAB = -Fg (a + b)                    (2)
Subsitusi persamaan 1 ke 2

Jawaban B

Soal No.3 (UTBK 2019)

Gas sebanyak n mol dan bersuhu T kelvin disimpan dalam sebuah silinder yang berdiri tegak. Tutup silinder berupa piston bermassa m kg dan luas penampang S m2 dapat bergerak bebas. Mula-mula piston diam dan tinggi kolom gas h meter. Kemudian, piston ditekan sedikit ke bawah sedalam y meter, lalu dilepas sehingga berosilasi. Jika suhu gas tetap, gas berperilaku sebagai pegas dengan konstanta pegas k, dan , tekanan gas sama dengan…. pascal

PEMBAHASAN :
Pada saat di tekan sebesar y, timbul gaya pulih untuk mengembalikan ke posisi semula. Yang berperilaku sebagai gaya pulih adalah gaya dorong gas.
Fpulih = Fgas
Jika Fpulih= k y
K y = Fgas
Dari konsep tekanan, P = F/A maka F = P A dengan demikian:
K y = Pgas A
Pgas = Ky/A
Perlu dingat, tekanan berkontribusi pada gaya pemulih itu adalah perbedaan tekanan sebelum dan sesudah ditekan ΔP dengan demikian, persamaan di atas:
ΔP = Ky/A                                (1)
Dari soal suhu gas dijaga konstan, akibatnya tekanan gas sebelum ditekan (P1) berbeda dengan tekanan gas sesudah di tekan (P2) dengan hubungan:
P2 = P1 + ΔP       (2)
Untuk situasi gas ideal suhu konstan sebagai berikut.
P1 V1 = P2 V2
P1 A h = P2 A (h-y)
P1 h = P2 (h-y)

Dari soal diperoleh hubungan:

Dengan demikian:

Jawaban A

Soal No.4
Benda bergetar selaras sederhana pada pegas dengan tetapan gaya 80 N/m. Amplitudo getaran tersebut 20 cm dan kecepatan maksimum sebesar 4m/s. massa benda tersebut bernilai …
  1. 1 kg
  2. 0.8 kg
  3. 0,4 kg
  4. 0,2 kg
  5. 0,1 kg

PEMBAHASAN :
get17
Jawaban : D

Soal No.5
Sebuah benda melakukan gerak harmonik sederhana dengan amplitudo A dan frekuensi sudut ω. Pada saat kecepatan benda sama dengan 4/5 kecepatan maksimumnya, percepatannya adalah …
  1. -(4/5)Aω2
  2. -(3/5)Aω2
  3. -(1/5)Aω2
  4. 3/5 Aω2
  5. 4/5 Aω2

PEMBAHASAN :
get18
Jawaban : B

Soal No.6
Bila pada simpangan y = 5 cm, percepatan gelombang selaras a = -5 cm/s2 maka pada saat simpangan 10 cm, percepatannya adalah … cm/s2.
  1. -25
  2. -20
  3. -10
  4. -2,5
  5. -1,25

PEMBAHASAN :
get19
Jawaban : C

Soal No.7
Suatu partikel bergetar selaras dengan amplitudo A cm dan periode T detik. Jika partikel mulai bergetar dari kedudukan seimbang dengan arah kanan maka partikel mempunyai simpangan sebesar 4/5 A cm dengan arah gerak ke kiri pada saat partikel telah bergetar selama waktu … detik
  1. T/12
  2. T/6
  3. T/4
  4. T/3
  5. 5T/12

PEMBAHASAN :
get20
Jawaban : E

Soal No.8
Pada ujung sebuah pegas (k = 5 N/m) digantungkan sebuah beban. Beban di tarik ke bawah sejauh 10 cm kemudian dilepaskan. Sejak dilepaskan beban melewati titik terendahnya 140 kali dalam selang waktu 44 sekon. Tentukanlah:
  1. Amplitudo
  2. Periode
  3. Frekuensi

PEMBAHASAN :
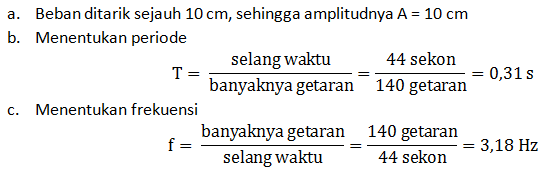
get21

Soal No.9
Sebuah bandul sederhana dengan massa beban 50 gram dan panjang tali 90 cm digantung pada langit-langit sebuah lift. Percepatan gravitasi 10 ms-2. Jika bandul digetarkan tentukan periode bandul ketika lift sedang bergerak:
  1. Ke atas dengan kecepatan tetap
  2. Ke atas dengan percepatan tetap 2 ms-2
  3. Ke bawah dengan percepatan tetap 2 ms-2

PEMBAHASAN :
get23

Soal No.10
Benda bermassa m digantung pada ujung sebuah pegas dan bergetar dengan periode 1 sekon. Kemudian pada benda tersebut ditambahkan massa 0,3 kg dan periodenya menjadi 2 sekon. Berapakah massa m?

PEMBAHASAN :
get24

Soal No.11
Sebuah kubus kayu bermassa 220 gram digantung vertikal pada ujung sebuah pegas yang memiliki tetapan 50 Nm-1. Sebutir peluru bermassa 25 gram ditembakkan vertikal ke atas tepat mengenai bagian bawah kayu dan bersarang di dalamnya. Berapakah periode getaran kayu tersebut? (π =22/7)

PEMBAHASAN :
get25

Soal No.12
Sebuah benda bermassa m digantungkan pada sebuah pegas dan bergetar dengan periode 0,5 sekon. Berapa bagiankah massa yang harus dikurangkan pada m agar frekuensinya menjadi dua kali semula?

PEMBAHASAN :
get26

Soal No.13
Sebuah bola dengan massa 20 gram digantung pada sepotong pegas. Kemudian ditarik ke bawah dari kedudukan setimbang lalu dilepaskan. Ternyata terjadi getaran tunggal dengan frekuensi 32 Hz. Jika bola tersebut diganti dengan massa bola 80 gram, berapakah frekuensi yang akan terjadi?

PEMBAHASAN :
get27

Soal No.14
Sebuah bandul sederhana panjangnya 39,2 cm.
  1. Berapakah periodenya di bumi (g = 9,8 ms-2)
  2. Berapakah periodenya di tempat yang percepatan gravitasinya empat kali percepatan gravitasi bumi?

PEMBAHASAN :
get28

Soal No.15
Berapakah panjang bandul sederhana yang bergetar 49 kali dalam selang waktu 44 sekon? (g = 9,8 ms-2 dan π = 22/7)

PEMBAHASAN :
get29

Soal No.16
Dua bandul sederhana masing-masing 60,5 cm dan 50 cm. Bandul 60,5 cm digetarkan frekuensinya 1 hertz. Jika bandul 50 cm digetarkan, berapakah frekuensinya?

PEMBAHASAN :
get30

Soal No.17
Sebuah bandul yang panjangnya 88,20 cm diberi simpangan kecil. Sebuah rintangan vertikal panjangnya 66,15 cm dipasang memanjang dari titik pusat bandul
get31
Berapa lama waktu yang diperlukan jika bandul dilepaskan dari A hingga kembali lagi ke A? (π= 3,14, g = 9,8 ms-2)

PEMBAHASAN :
get32

Soal No.18
Berikut ini merupakan prinsip gerak harmonis yang digunakan sebagai peredam kejut adalah …
  1. Pendulum
  2. Ayunan
  3. Shock pegas mobil
  4. Alat musik
  5. Bungee jumping

PEMBAHASAN :
Pegas (shocker) dipasang pada roda mobil untuk memastikan perjalanan yang aman bagi penumpang. Ketika mobil menabrak jalan bergelombang, pegas akan berfungsi sebagai peredam kejut sehingga perjalanan menjadi mulus. Gaya pemulihan pada pegas akan mendorong roda mobil kembali ke tempatnya.
Jawaban : C

Soal No.19
Syarat suatu gerak dinamakan getaran harmonik adalah …
  1. Gerakan dinamik
  2. Gerakannya selalu melewati posisi keseimbangan
  3. Percepatan berbanding terbalik dengan posisi benda
  4. Gaya mengarah ke posisi keseimbangan
  5. Gerakan benda berubah-ubah

PEMBAHASAN :
Syarat getaran harmonik sederhana, sebagai berikut:

  1. Gerakannya periodik (bolak-balik)
  2. Gerakannya selalu melewati posisi keseimbangan
  3. Percepatan/ gaya yang bekerja pada benda sebanding dengan posisi/ simpangan benda
  4. Arah percepatan/ gaya yang bekerja pada benda selalu mengarah ke posisi keseimbangan

Jawaban : B

Soal No.20
Penyebab benda mengalami percepatan pada gerak harmonik adalah …
  1. Massa benda
  2. Gaya sentripetal
  3. Periode getaran
  4. Frekuensi getaran
  5. Gaya pulih

PEMBAHASAN :
Pada gerak harmonik sederhana, benda mengalami percepatan dengan arah menuju titik setimbang. Percepatan tersebut terjadi karena adanya gaya pulih. Besarnya gaya pemulih bergantung kepada posisi benda yang berosilasi.

Jawaban : E

2 comments

  1. AlTof Yuri
    09/04/2017 at 12:52 pm

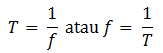
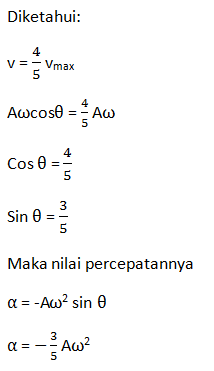
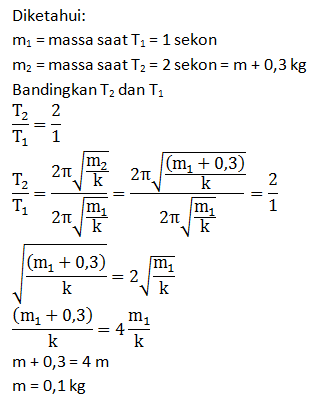
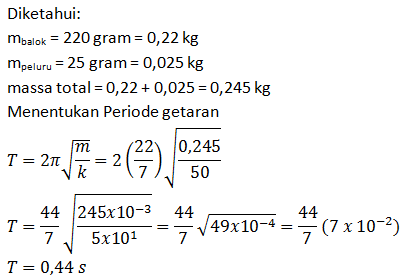
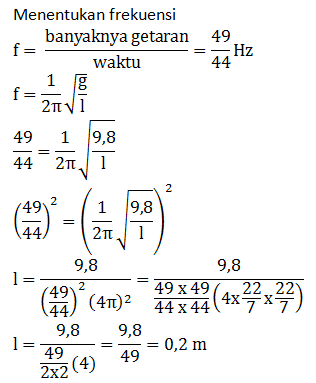
    thankssss

    Reply
  2. OneTorch
    26/02/2018 at 2:11 pm

    Kasih contoh soal yang tentang bandul fisis dong..
    Yg ada pengaruhnya dengan gaya torsi. Makasih

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.

You cannot copy content of this page