Rangkuman Logika Matematika Kelas 11

Operasi Logika

Operasi pada logika matematika ada 5, yaitu:

1. Negasi/ ingkaran ( bukan …)
   Negasi atau ingkaran apabila dari sebuah pernyataan dapat membubuhkan kata tidak benar atau dapat menyisipkan kata bukan. Jika P adalah sebuah pernyataan, maka negasi/ ingkarannya dapat ditulis ∼P.
2. Disjungsi (… atau …)
   Disjungsi apabila pernyataan yang dibentuk dari dua pernyataan, misalkan p dan q yang dirangkaikan menggunakan kata hubung atau. Dapat dilambangkan p ∨ q, dibaca p atau q.
3. Konjungsi (… dan ….)
   Konjungsi apabila pernyataan yang dibentuk dari dua pernyataan, misalkan p dan q yang dirangkaikan menggunakan kata hubung dan. Dapat dilambangkan p ∧ q, dibaca p dan q.
4. Implikasi (jika … maka …)
   Implikasi bisa diartikan dengan pernyataan bersyarat/ kondisional, apabila pernyataan majemuk disusun dari dua buah pernyataan. Misalkan jika p maka q dilambangkan p ⇒ q.
5. Biimplikasi/implikasi dwiarah (jika dan hanya jika …)
   Biimpikasi apabila pernyataan dapat dirangkai dengan menggunakan kata hubung “ jika dan hanya jika”. Misalkan p jika dan hanya jika q dilambangkan p⇔q

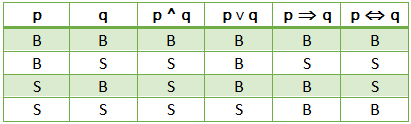
Tabel Kebenaran

Kuantor

Suatu ungkapan yang diterapkan pada kalimat terbuka dengan satu variabel dan dapat mengubahnya menjadi kalimat tertutup disebut kuantor. Ada 2 macam Kuantor, yaitu:

1. Kuantor Universal 
   Suatu pernyataan yang berlaku untuk umum, dilambangkan   dibaca “untuk semua nilai x”.
2. Kuantor Eksistensial
   Suatu pernyataan yang berlaku secara khusus, dilambangkan  dibaca “ada nilai x” atau “beberapa nilai x”.

Negasi pernyataan majemuk

Konvers, Invers, dan Kontraposisi

Hubungan nilai kebenaran dari suatu implikasi p   q diperoleh:

1. q ⇒ p disebut konvers dari p ⇒ q
2. ~ p⇒ ~ q disebut invers dari p ⇒ q
3. ~ q ⇒ p disebut kontraposisi dari p ⇒ q

Ekuivalensi

Dua pernyataan majemuk dikatakan ekuivalen jika kedua pernyataan itu mempunyai nilai kebenaran yang sama. Pernyataan  ekuivalensi ada dua, yaitu:

1. p ⇒ q ≡ ~ p v q
2. p ⇒ q ≡ ~q ⇒ p

Penarikan Kesimpulan

Proses penarikan kesimpulan dari beberapa pernyataan yang diketahui nilai kebenarannya disebut premis. cara menarik kesimpulan dari 2 premis sebagai berikut:

1. Modus Ponens (Kaidah Pengasingan)
   Premis 1 : p ⇒ q
   Premis 2 : p
   Kesimpulan : q
2. Modus Tolens (Kaidah Penolakan Akibat)
   Premis 1 : p ⇒ q
   Premis 2 : ~q
   Kesimpulan : ~p          
3. Silogisme (Sifat Menghantar atau Transitif)
   Premis 1 : p ⇒ q
   Premis 2 : q ⇒ r
   Kesimpulan : p ⇒ r

Contoh Soal & Pembahasan Logika Matematika Kelas 11

1. Pada hari Sabtu siswa SMP memakai baju pramuka dan tidak memakai atribut lengkap
2. Pada hari Sabtu siswa SMP tidak memakai seragam pramuka atau tidak memakai atribut lengkap
3. Pada hari Sabtu siswa SMP tidak memakai seragam pramuka dan atribut lengkap
4. Selain hari Sabtu siswa SMP tidak memakai seragam pramuka dan memakai atribut lengkap
5. Selain hari Sabtu siswa SMP memakai seragam pramuka atau atribut lengkap

PEMBAHASAN :
“ Pada hari sabtu siswa SMP memakai baju pramuka dan atribut lengkap “
Ingkaran dari pernyataan di atas:
~ (p ∧ q) ≡ ~ p ∨ ~ q
Maka: “ Pada hari Sabtu siswa SMP tidak memakai seragam pramuka atau tidak memakai atribut lengkap “.
Jawaban : B

1. (p ⇒ ~ q) ⇒ (p ⇒ q)
2. (~ p ⇒ ~ q) ⇒ (p ∧ ~ q)
3. (p ∧ q) ⇒ (p ⇒ ~ q)
4. (p ∧ ~ q) ⇒ (~ p ∧ ~ q)
5. (p ⇒ ~ q) ⇒ (p ⇒ ~ q)

PEMBAHASAN :
Berlaku:
Kontraposisi dari a ⇒ b adalah ~ b ⇒ ~ a
Sehingga kontraposisi dari (~ p ⇒ q) ⇒ (~ p ∨ q) sebagai berikut:
~ ( ~ p ∨ q) ⇒ ~ ( ~ p ⇒ q) ≡ (p ∧ ~ q) ⇒ (~ p ∧ ~ q)
Jawaban : D

1. (p ∨ ~ q) ⇒ ~ p
2. (~ p ∨ q) ⇒ ~ p
3. (~p ∨ ~ q) ⇒ p
4. ~ p ⇒ (p ∨ ~ q)
5. ~ p ⇒ (p Ù ~ q)

PEMBAHASAN :
Berlaku:
Invers dari a ⇒ b adalah ~ a ⇒ ~ b
Sehingga invers dari (p ∧ ~ q) ⇒ p sebagai berikut:
~ (p ∧ ~ q) ⇒ ~ p ≡ (~ p ∨ q) ⇒ ~ p
Jawaban : B

1. Jika harga BBM tidak naik maka harga barang naik
2. Jika harga barang naik maka harga BBM naik
3. Harga BBM naik dan harga barang tidak naik
4. Harga BBM naik atau harga barang naik
5. Harga barang naik jika dan hanya jika harga BBM naik

PEMBAHASAN :
Berlaku: ~ (p ⇒ q) ≡ p ∧ ~ q
“ Jika harga BBM naik, maka harga barang naik “
Sehingga ingkaran atau negasi dari pernyataan di atas adalah “ Harga BBM naik dan harga barang tidak naik “.
Jawaban : C

1. Konjungsi
2. Disjungsi
3. Implikasi
4. Biimplikasi
5. Negasi

PEMBAHASAN :
Konjungsi adalah suatu pernyataan majemuk yang dihubungkan oleh kata hubung ‘ dan ‘. Dilambangkan dengan p ∧ q yang berarti p dan q.
Jawaban : A

1. Jika Budi sakit, berarti Budi kehujanan
2. Jika Budi demam, berarti Budi sakit
3. Jika Budi kehujanan, maka Budi sakit
4. Jika Budi kehujanan, maka Budi demam
5. Jika Budi kehujanan, maka Budi sakit dan demam

PEMBAHASAN :
Hujan ⇒ sakit
Sakit ⇒ demam
Jadi kesimpulannya adalah “Jika Budi kehujanan, maka Budi Demam.”
Jawaban : D

1. Semua buruh demo dan lalu lintas selalu macet
2. Semua buruh demo dan lalu lintas tidak macet
3. Semua buruh tidak demo dan lalu lintas macet
4. Semua buruh tidak demo dan lalu lintas tidak macet
5. Semua buruh tidak demo dan lalu lintas selalu macet

PEMBAHASAN :
Buruh ⇒ demo ⇒ macet
Ingkaran: Buruh ⇒ demo ∼ macet
Jadi ingkaran dari pernyataan di atas adalah: ” Semua buruh demo dan lalu lintas tidak macet. ”
Jawaban : B

1. Maya tidak suka memakai keduanyas
2. Maya tidak memakai bando dan memakai pita
3. Maya memakai bando dan tidak memakai pita
4. Maya tidak memakai bando dan pita
5. Maya memakai bando dan pita

PEMBAHASAN :
p: Maya memakai bando
q: Maya memakai pita
Jadi pernyataan majemuk dari hasil penggabungan pernyataan di atas adalah: ” Maya memakai bando dan pita. ”
Jawaban : E

1. Semua orang tidak disiplin olah raga dan Ratna bukan orang sehat
2. Semua orang tidak disiplin olah raga dan Ratna orang sehat
3. Semua orang disiplin olah raga dan Ratna bukan orang sehat
4. Semua orang disiplin olah raga dan Ratna orang sehat
5. Semua orang disiplin olah raga dan Ratna selalu sehat

PEMBAHASAN :
p: Semua orang disiplin olah raga
q: Ratna orang sehat
∼ (p – q) = (∼ p ∨ q) = (p ∧ ∼ q)
Jadi kesimpulan negasinya adalah: ” Semua orang disiplin olah raga dan Ratna bukan orang sehat.”
Jawaban : C

1. Konjungsi
2. Negasi
3. Disjungsi
4. Implikasi
5. Biimplikasi

PEMBAHASAN :
p: 9 merupakan bilangan ganjil (benar)
q: 9 habis dibagi 2 (salah)
Jadi p ∧ q merupakan konjungsi, hanya bernilai benar jika kedua pernyataan bernilai benar. Sedangkan pernyataan di atas salah satunya bernilai salah.
Jawaban : A