DAFTAR ISI
Rangkuman Trigonometri Kelas X/10
UKURAN SUDUT
Perbandingan trigonometri dalam segitiga siku-siku
Sudut dan Kuadran
Pembagian daerah
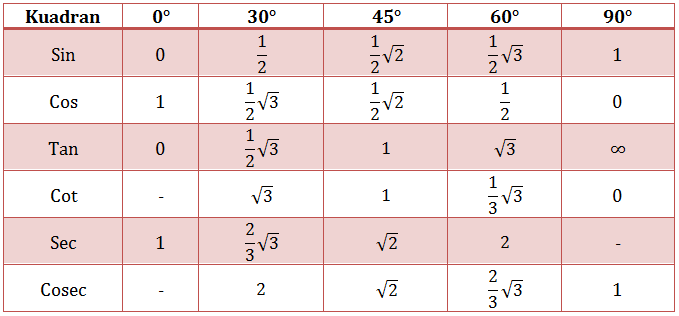
Tanda-tanda Perbandingan Trigonometri
Sudut-sudut Khusus
Rumus trigonometri Sudut-sudut berelasi
Sudut (90o - a)
Sin (90o - a) = Cos a Cot (90o - a) = tan a
Cos (90o - a) = Sin a Sec (90o - a) = cosec a
Tan (90o - a) = Cot a Cosec (90o - a) = Sec a
Sudut (90o + a)
Sin (90o + a) = cos a Cot (90o + a) = -tan a
Cos (90o + a) = -sin a Sec (90o + a) = -cosec a
Tan (90o + a) = -cot a Cosec (90o + a) = sec a
Sudut (180o - a)
Sin (180o - a) = sin a Cot (180o - a) = -cot a
Cos (180o - a) = -cos a Sec (180o - a) = -sec a
Tan (180o - a) = -tan a Cosec (180o - a) = cosec a
Sudut (180o + a)
Sin (180o + a) = -sin a Cot (180o + a) = cot a
Cos (180o + a) = -cos a Sec (180o + a) = -sec a
Tan (180o + a) = tan a Cosec (180o + a) = -cosec a
Sudut (270o - a)
Sin (270o - a) = -cos a Cot (270o - a) = tan a
Cos (270o - a) = -sin a Sec (270o - a) = -cosec a
Tan (270o - a) = cot a Cosec (270o - a) = -sec a
Sudut (270o + a)
Sin (270o + a) = -cos a Cot (270o + a) = -tan a
Cos (270o + a) = sin a Sec (270o + a) = cosec a
Tan (270o + a) = -cot a Cosec (270o + a) = -sec a
Sudut (-a)
Sin (-a) = -sin a Cot (-a) = -cot a
Cos (-a) = cos a Sec (-a) = sec a
Tan (-a) = -tan a Cosec (-a) = -cosec a
Sudut (n.360o - a)
Sin (n.360o - a) = Sin (-a) = -sin a Cot (n.360o - a) = Cot (-a) = -cot a
Cos (n.360o - a) = Cos (-a) = cos a Sec (n.360o - a) = Sec (-a) = sec a
Tan (n.360o - a) = Tan (-a) = -tan a Cosec (n.360o - a) = Cosec (-a) = -cosec a
Sudut (n.360o + a)
Sin (n.360o + a) = sin a Cot (n.360o + a) = cot a
Cos (n.360o + a) = cos a Sec (n.360o + a) = sec a
Tan (n.360o + a) = tan a Cosec (n.360o + a) = cosec a
Dalil Segitiga
Aturan Sinus
Aturan Cosinus
Aturan Tangen
Luas Segitiga
Identitas Trigonometri
Hubungan Kebalikan
Hubungan Ekuivalen
Hubungan teorema Phytagoras
Penjumlahan dan Selisih Dua Sudut
Sudut Rangkap
Jumlah dan Selisih Sinus dan Cosinus
Rumus Perkalian Sinus dan Cosinus
- 2 sin A cos B = sin (A+B) + sin (A – B)
- 2 cos A sin B = sin (A+B) – sin (A – B)
- 2 sin A cos B = cos (A+B) + cos (A – B)
- – 2 sin A sin B = cos (A+B) – cos (A – B)
Persamaan Trigonometri
- sin x = sin a ⇒ x = a+ k.2p atau x = (p-a) + k.2p
- cos x = cos a ⇒ x = ±a + k. p
- tan x = tan a ⇒ x = a + k. p ; k = bilangan bulat
Contoh Soal & Pembahasan Trigonometri Kelas X/10
- α = -β + 45o
- α = -β + 60o
- α = -β + 90o
- α = -β + 120o
- α = -β + 180o
PEMBAHASAN :
x = sin α + sin β ⇒ x2 = sin2 α + 2sin α. sin β + sin2 β
y = cos α - cos β ⇒ y2 + = cos2 α - 2cos α. cos β + cos2 β +
………………………..x2 + y2 = 1-2(cos α. cos β - sin α. sin β) + 1
⇒ x2 + y2 = 2 - 2 cos (α + β)
∴ Nilai terbesar x2 + y2 terjadi saat:
cos (α + β) = -1
⇒ cos (α + β) = cos 180o
⇒ α + β = 180o
⇒ α = -β + 180o
Jawaban E
PEMBAHASAN :
cos 2x + cos 2y = ![]()
⇒ (1 - 2 sin2 x) + (1 - 2 sin2 y) = ![]()
⇒ 2 - 2 sin2 x - 2 (2 sin x)2 = ![]()
⇒ -10. sin2 x = ![]()
⇒ sin2 x = ![]()
⇒ sin x = ![]()
Sin y = 2. sin x
⇒ sin y = 2. ![]()
⇒ sin y = ![]()
![]()
Jawaban B
- 8√2
- 8√3
- 16
- 8√5
- 8√6
- 5/8
- 25/32
- 5/32 √39
- 25/32 √39
- 5/32
- 55√2
- 60√2
- 75√3
- 90√3
- 120√3
Jawaban : D
- 1/4
- 1/2
- 3/4
- 1
- 5/4
- -7 + 4 √3
- 7 + 4√3
- 7 - 4√3
- -7 - 4√3
- -7 + 2√3
- -3/5
- -2/5
- -1/5
- 1/5
- 3/5
- ½ √3
- ½ √2
- ½
- - ½
- - ½ √2
- tan2 θ + sin2 θ
- tan2 θ - sin2 θ
- sin2 θ - cos2 θ
- cos2 ½θ + tan2 ½θ
- sin2 ½θ + tan2 ½θ
- -√3
- -½√3
- -1/3√3
- 1/3√3
- √3
- 17/25
- 1
- 6/5
- 31/25
- 7/5
- 72/125
- 96/125
- 108/125
- 124/125
- 144/125
- ½
- ½ √2
- ½ √3
- √3
- 1
PEMBAHASAN :
- 3 sin A + 4 cos B = 6
9 sin2 A + 24 sin A cos B + 16 cos2 B = 36…( 1 )
3 cos A + 4 sin B = 1
9 cos2 A + 24 cos A sin B + 16 sin2 B = 1….( 2)
Dari persamaan (1) dan (2)
9sin²A +24 sinA cosB + 16 cos²B =36
9cos²A + 24 cosA sinB + 16 sin²B = 1
9 + 24 (sinA sinB + cosA sinB) + 16 = 37
sinA cosB + cosA sinB =24/12 = ½
- ∠A + ∠B + ∠C = ∠180°
sin C = sin (180° - (A + B))
=sin (A + B)
=sinA cosB + cosA sinB
= ½
Jawaban : A
PEMBAHASAN :
Diketahui A, B, dan C sudut – sudut dalam segitiga ABC. Jika cos A = 4/5 dan sin B = 1/√5 , maka nilai sin C = …
- -½ √5
- -2/5 √5
- 1/25 √5
- 1/5 √5
- 2/5 √5
- 4
- 3
- 2
- 1
- 0
- (45,135)
- (135,180)
- (45,225)
- (135,225)
- (135,315)
- (450, 1350)
- (600, 1650)
- (450, 1800)
- (600 , 1800)
- (1350, 1800)
- {60 ˂ x˂ 180}
- {x ≤ 60 atau x ≥ 180}
- {0 ˂ x ˂ 60 atau 300 ˂ x ˂ 360}
- {0˂ x ˂ 60 atau 300 ˂ x ≤ 360}
- {60 ≤ x ≤ 180}
- 3/2 < k < 2
- 3/2 < k < 2 atau k < 0
- 1/2 < k < 2
- 1/2 < k < 1 atau k < 0
- 0 < k < 3/2
- {x│20 ≤ x≤ 100}
- {x│ 35 ≤ x ≤ 100}
- {x│ x≤ 50 atau x ≥ 130}
- {x│≤ 35 atau x≥ 145}
- {x│x ≤ 50 atau x ≥ 310}
- 0° < x < 120°, 180° < x < 240°
- 0° < x < 150°, 180° < x < 270°
- 120° < x < 180°, 240o < x < 360°
- 150° < x < 180°, 270° < x < 360°
- 0° < x < 135°, 180° < x < 270°
PEMBAHASAN :
Jawaban : B
PEMBAHASAN :
Jawaban : A
- 30(1 -
 )
) - 90(1 + 2
 )
) - 30(2 -
 )
) - 60(1 +
 )
) - 20(3 + 2
 )
)
PEMBAHASAN :
∠P + ∠R = 900
x + x = 900
2x = 900
x = 450
PQ = PR . sin x
. = 60 . sin 450
. = 60 . ½![]()
. = 30![]()
QR = PR . cos x
. = 60 . cos 450
. = 60 . ½![]()
. = 30![]()
Maka keliling ΔPQR dapat dihitung sebagai berikut:
K ΔPQR = PQ + PR + QR
. = 30![]() + 60 + 30
+ 60 + 30![]()
. = 60 + 60![]()
. = 60(1 + ![]() )
)
Jawaban : D
- ½
- -1/3
- -¼
- -½
- 1/5
PEMBAHASAN :
θ = 3/2
θ = 3/2 x 1800 = 2700
sin 2700 = sin (1800 + 900) = 0 + 1 = 1
cos 2700 = cos (1800 + 900) = -1 + 0 = -1
tan 2700 = tan (1800 + 900) = 0
Maka ¼ sin θ cos θ - tan θ = ¼ sin 2700 cos 2700 - tan 2700
. = ¼ . 1 . -1 – 0 = -¼
Jawaban : C
PEMBAHASAN :
Diagonal bidang AC = BD = 4p![]()
OB = ½ BD = ½ . 4p![]() = 2p
= 2p![]()
OX = ½ OC = AC = . 4p![]() = p
= p![]()
Maka sin ∠XBO dapat dihitung sebagai berikut:
Jawaban : E
- 1
- 2
- 3
- 4
- 5
PEMBAHASAN :
Berlaku sin2 a + cos2 a = 1
Sin 200 = sin (900 – 700 ) = cos 700
Sin 500 = sin (900 – 400) = cos 400
Maka soal di atas dapat diselesaikan sebagai berikut:
Sin2 (200) + sin2 (500) + sin2 (700) + sin2 (400)
= Cos2 (700 ) + cos2 (400) + sin2 (700) + sin2 (400)
= {Cos2 (700 ) + sin2 (700)} + { cos2 (400) + sin2 (400)}
= 1 + 1
= 2
Jawaban : B
- 11
- 20
- 13
- 17
- 25
PEMBAHASAN :
Berlaku sin2 α + cos2 α = 1
Misalkan:
p = sin α
q = cos α
p + q = 2
(p + q)2 = 4
P2 + 2pq + q2 = 4
(p2 + q2) + 2pq = 4
1 + 2pq = 4
2pq = 3
pq = 3/2
Maka sin3 α + cos3 α
= p3 + q3
= (p + q)3 + 3p2q + 3pq2
= (p + q)3 + 3pq(p + q)
= 23 + 3.3/2(2)
= 8 + 9
= 17
Jawaban : D
PEMBAHASAN :
Jawaban : A
PEMBAHASAN :
Jawaban : E
- 1 – sin x
- 1 + tan x
- 1 + cos x
- ½ - sin x
- ½ - cos x
PEMBAHASAN :
Jawaban : C
- 10 cm
- 6 cm
- 13 cm
- 8 cm
- 11 cm
PEMBAHASAN :
Maka panjang sisi segi enam beraturan tersebut dapat dihitung sebagai berikut:
Misalkan:
Panjang sisi = a
Jawaban : B
PEMBAHASAN :
Diketahui:
a = 3
b = 3
c = 4
Jawaban : A
PEMBAHASAN :
Luas ΔPQR = ½ . PR . PQ . sin ∠RPQ
20 = ½ . 10 . 8 . sin P
20 = 40
Sin ∠RPQ =
∠RPQ = 300
Maka cos ∠RPQ = ½
Jawaban : D
- 1
- 2
- 3
- 4
- 5
PEMBAHASAN :
Luas Δ = ½ . alas . tinggi
12 = ½ . 12 . 6 sin α
12 = 36 sin α
Maka terdapat 4 nilai a pada segitiga tersebut
Jawaban : D
- ¼
 (1 -
(1 - )
- ½
 (1 +
(1 + )
- ¼ (
 -
- )
- 2
 (1 +
(1 + )
 (1 -
(1 - )
PEMBAHASAN :
tan a = , a = 300
tan b = 1 , b = 450
sin a = ½
cos a = ½
sin b = ½![]()
cos b = ½ ![]()
sin (a – b) = sin a . cos b – cos a . sin b
= ½ . ½ ![]() – ½
– ½ . ½
![]()
= ¼ ![]() – ¼
– ¼
= ¼ ![]() (1 -
(1 - )
Jawaban : A
PEMBAHASAN :
Diketahui
cos ∠A =
→ sin ∠A =
cos ∠B =
→ sin ∠B =
Maka sin ∠C dapat dihitung sebagai berikut:
Sin ∠C = sin {1800 – (A + B)}
= sin (A + B)
= (sin A . cos B) + (cos A . sin B)
Jawaban : B
- 300
- 400
- 500
- 600
- 900
PEMBAHASAN :
cos 250 cos 350 - sin 250 cos 350
= cos (250 + 350)
= cos 600
= cos (900 – 600)
= sin 300
Jawaban : A
PEMBAHASAN :
α - β = ½ π
Cos (α - β) = cos ½ π
Cos α cos β + sin α . sin β = ½
Cos α cos β + ![]() = ½
= ½
Cos α cos β =
cos (α + β) = Cos α cos β - sin α . sin β
Jawaban : E
PEMBAHASAN :
Diketahui:
sin α - sin β =
cos α + cos β =
Persamaan 1:
sin α - sin β = (kuadratkan)
sin2 α - 2 sin α sin β + sin2 β = P
Persamaan 2:
cos α + cos β = (kuadratkan)
cos2 α + 2 cos α cos β + cos2 β = Q
Berlaku:
sin2 x + cos2 x = 1
Jumlahkan persamaan 1 dan 2 sebagai berikut:
(sin2 α + cos2 α) + 2(cos α cos β - sin α sin β) + (sin2 β + cos2 β) = P + Q
1 + 2(cos α cos β - sin α sin β) + 1 = P + Q
2 + 2 cos (α + β) = P + Q
Cos (α + β) =
Jawaban : B
PEMBAHASAN :
Jawaban : E
PEMBAHASAN :
Jawaban : A
-
- 1
PEMBAHASAN :
2 sin α cos β = sin (α + β) + sin (α - β)
2 sin 300 cos 300 = sin (300 + 300) + sin (300 – 300)
2 sin 300 cos 300 = sin 600 + sin 00
2 sin 300 cos 300 = + 0
2 sin 300 cos 300 =
Jawaban : D
- – sin B
- – 5 cos B
- sin A + sin B
- sin A – sin B
- cos (A + B)
PEMBAHASAN :
5 sin A sin B = 5 x ½ {cos (A – B) – cos (A + B)}
5 sin A sin B = 5 x ½ (cos A – cos B – cos A – cos B)
5 sin A sin B = 5 x ½ (- 2 cos B)
5 sin A sin B = - 5 cos B
Jawaban : B
PEMBAHASAN :
sin 900 + sin 300 = 2 sin ½ (900 + 300 ) . cos ½ (900 – 300)
sin 900 + sin 300 = 2 sin ½ (1200) . cos ½ (600)
sin 900 + sin 300 = 2 sin 600 . cos 300
sin 900 + sin 300 = 2 ..
sin 900 + sin 300 = ![]()
Jawaban : A
PEMBAHASAN :
Berlaku:
Sin 2α = 2 sin α cos α
Segitiga dengan tipe teorema Pythagoras, maka cos α =
Sin 2α = 2 sin α cos α
Sin 2α = 2 . .
Sin 2α =
Jawaban : E
PEMBAHASAN :
Jawaban : D
PEMBAHASAN :
Sin P cos Q = ½ {sin (P + Q) + sin (P – Q)}
Sin P cos Q = ½ {sin (1800 – C) + sin 600 }
Sin P cos Q = ½(sin C +)
Sin P cos Q = ½( +
)
Sin P cos Q =
Jawaban : C
- 0
- 1
- ½
PEMBAHASAN :
Jawaban : A
- 00 dan 300
- 00 dan 600
- 200 dan 500
- 300 dan 450
- 450 dan 900
PEMBAHASAN :
sin 2x – sin x = 0
2 sin x cos x – sin x = 0
sin x (2 cos x – 1) = 0
sin x = 0 → x = 00
2 cos x – 1 = 0
2 cos x = 1
cos x = ½ → x = 600
Jawaban : B
- 900
- 600
- 1200
- 2700
- 1800
PEMBAHASAN :
(2 cos2 x – 1) – cos x – 2 = 0
2 cos2 x – cos x – 3 = 0
Misalkan:
cos x = a
Berlaku:
-1 ≤ cos x ≤ 1
Maka 2 cos2 x – cos x – 3 = 0 → 2a2 – a – 3 = 0
(2a – 3)(a + 1) = 0
2a – 3 = 0
2a = 3
a = 3/2 (tidak memenuhi)
a + 1 = 0
a = - 1 (memenuhi)
cos x = - 1
x = 1800
Jawaban : E
- 1350 dan 2250
- 900 dan 2700
- 1800 dan 1800
- 1500 dan 2100
- 1200 dan 2400
PEMBAHASAN :
+ 2 cos x = 0
2 cos x = -
cos x = - ½
x1 = 1500
x2 = 2100
Jawaban : D
PEMBAHASAN :
Jawaban : C
- 300
- 600
- 900
- 1200
- 1500
PEMBAHASAN :
Jawaban : A
- {450 , 1350 , 2250 , 3150 }
- {300 , 600 , 1800 , 2700 }
- {600 , 1200 , 1800 , 2400 }
- {00 , 450 , 1350 , 2250 }
- {900 , 1800 , 2700 , 3600 }
PEMBAHASAN :
→ kalikan cos x
2 cos2 x - 2![]() cos x + 1 = 0
cos x + 1 = 0
( ![]() cos x – 1)2 = 0
cos x – 1)2 = 0
( ![]() cos x – 1) (
cos x – 1) (![]() cos x – 1) = 0
cos x – 1) = 0
![]() cos x – 1 = 0
cos x – 1 = 0
cos x = ± ½ ![]()
kuadran I → x = 450
kuadran II → x = 1350
kuadran III → x = 2250
kuadran IV → x = 3150
Jawaban : A
- 300 dan 600
- 00 dan 900
- 450 dan 450
- 600 dan 1200
- 900 dan 900
PEMBAHASAN :
4 cos4 x – 4 cos2 x = 0
4 cos2 x (cos2 x – 1) = 0
4 cos2 x = 0
cos x = 0
x = 900
cos2 x – 1 = 0
cos x = 1
x = 00
Jawaban : B
- 0
- 1
- – ½
- – 1
- 2
PEMBAHASAN :
Berlaku:
y = a sin kx + c
nilai y minimum = - |a|+ c
f(x) = 3 sin (x - ) + 2
a = 3
c = 2
Maka nilai y minimum = - |3|+ 2 = - 1
Jawaban : D
- {x|67,50 ≤ x ≤ 112,50}
- {x|1350 ≤ x ≤ 2250}
- {x|900 ≤ x ≤ 1200}
- {x|450 ≤ x ≤ 1250}
- {x|300 ≤ x ≤ 1500}
PEMBAHASAN :
2 cos 2x0 + ![]() ≤ 0
≤ 0
cos 2x0 = -½![]()
2x0 = 1350 dan 2250
x0 = 67,50 dan 112,50
Maka nilai yang memenuhi 67,50 ≤ x ≤ 112,50
Jawaban : A
- {600 , 3000}
- {1200 , 2400}
- {900 , 2700}
- {1800 , - 1800}
- {- 900 , - 2700}
PEMBAHASAN :
sin (x + 600 ) + cos (x + 600) = 0
sin (x + 600 ) = - cos (x + 600)
berlaku:
cos x = sin (x – 900) atau sin(x + 900)
tan (x + 600) = tan 1500
x + 600 = 1500 ± k.1800
x = 900 ± k.1800
k = 0 → x = 900 (memenuhi)
k = 1 → x = - 900 (tidak memenuhi) atau x = 2700 (memenuhi)
k = 2 → x = - 2700 (tidak memenuhi) atau 4500 (tidak memenuhi)
Maka himpunan penyelesaiannya = {900 , 2700}
Jawaban : C
PEMBAHASAN :
Jawaban : E
- y = 2 cos (2x - 20o)
- y = 2 cos (x - 20o)
- y = 2 cos (2x - 10o)
- y = 2 cos (x - 10o)
- y = 2 cos (2x - 40o)
PEMBAHASAN :
Jawaban : A
PEMBAHASAN :
Bentuk umum persamaan kurva pada grafik di atas adalah y = 2 sin x. Kurva tersebut bergeser ke kiri sejauh . Maka persamaannya menjadi:
Jawaban : B
- -1
- 0
- 1
- 2
- 3
PEMBAHASAN :
Bentuk umum dari persamaan tersebut adalah y = a sin kx + c
a = 3
c = 2
Untuk menghitung nilai y minimum sebagai berikut:
Nilai minimum = - |a|+ c = - 3 + 2 = - 1
Jawaban : A
- 10
- 14
- 16
- 20
- 30
PEMBAHASAN :
F(x) = cos 2x + 2
a =
c = 2
Nilai maksimum F(x) = p = |a| + c = + 2
Nilai minimum F(x) = q = - |a| + c = - + 2
Maka:
p2 + q2 = (+ 2 )2 + (-
+ 2 )2
(3 + 4+ 4 ) + (3 - 4
+ 4 )
= 14
Jawaban : B
- 20
- 18
- 28
- 32
- 40
PEMBAHASAN :
Jawaban : D
- 10 dan 5
- 12 dan 4
- 22 dan 2
- 18 dan 8
- 26 dan 10
PEMBAHASAN :
Jawaban : C
- 1050 dan 3450
- 900 dan 1800
- 450 dan 1350
- 1200 dan 2400
- 750 dan 2250
PEMBAHASAN :
![]() sin x +
sin x + ![]() cos x = 1
cos x = 1
Kalikan persamaan di atas dengan ½, sehingga:
½![]() sin x + ½
sin x + ½![]() cos x = ½
cos x = ½
sin 450 sin x + cos 450 cos x = cos 600
cos (x – 450) = cos 600
Maka diperoleh:
x – 450 = ± 600 + k . 3600
x1 – 450 = 600 + k . 3600
x1 = 1050 + k . 3600
k = 0 → x1 = 1050 + k . 3600 → x1 = 1050 + 0 . 3600 = 1050 (memenuhi)
k = 1 → x1 = 1050 + k . 3600 → x1 = 1050 + 1 . 3600 = 4650 (tidak memenuhi)
x2 – 450 = - 600 + k . 3600
x2 = - 150 + k . 3600
k = 0 → x2 = - 150 + k . 3600 → x2 = - 150 + 0 . 3600 = - 150 (tidak memenuhi)
k = 1 → x2 = - 150 + k . 3600 → x2 = - 150 + 1 . 3600 = 3450 (memenuhi)
Jawaban : A
- {600 , 3000}
- {450 , 1800}
- {00 , 3600}
- {00 , 900}
- {1200 , 2400}
PEMBAHASAN :
tan (30 – ½ x)0 = cot (x + 60)0
tan (30 – ½ x)0 = tan (90 – (x + 60))0
tan (30 – ½ x)0= tan (- x + 30)0
300 – ½ x = - x + 300 + k . 1800
x – ½ x = k . 1800
½ x = k . 1800
x = k . 3600
k = 0 → x = k . 3600 → x = 00
k = 1 → x = 1 . 3600 → x = 3600
Maka Hp = {00 , 3600}
Jawaban : C
PEMBAHASAN :
Diketahui:
Untuk segitiga lancip berlaku rumus sebagai berikut:
cos γ = - cos (α + β)
sin γ = sin (α + β)
sin γ = sin α.cos β + cos α.sin β
Jawaban A
- 1
- 2
- -1
- ½
- -½
PEMBAHASAN :
Jawaban : C
PEMBAHASAN :
Diketahui:
∠P dan ∠Q lancip
Nilai dari tan (P-Q) dapat dihitung sebagai berikut:
Jawaban B
- 900
- 600
- 1200
- 450
- 1800
PEMBAHASAN :
, 00 < x < 1800
Identitas trigonometri:
1 + tan2 x = sec2 x
tan2x = sec2x - 1
cos x = 0
x = 900
Jawaban : A
PEMBAHASAN :
Diketahui:
cos A . cos B =
cos (A-B) =
cos A . cos B + sin A . sin B =
+ sin A . sin B =
sin A . sin B = -
=
Maka tan A . tan B dapat dihitung sebagai berikut:
Jawaban B
PEMBAHASAN :
Diketahui:
sudut a terletak di kuadran II
Jawaban E
- 1
- 0
- -2
- ½
- -1
PEMBAHASAN :
2 sin2 x + 3sin x - 2 = 0
(2 sin x – 1)(sin x + 2) = 0
sin x = ½ dan sin x = -2
Terletak di kuadran I, maka nilai yang sesuai adalah sin x = ½
tan x =
cos x =
Maka
Jawaban D
- 1
PEMBAHASAN :
Diketahui:
L Δ PQR = 18 cm2
Panjang PR = 6 cm
Panjang PQ = 12 cm
L = ½ . PQ . PR . sin P
18 = ½ . 12 . 6 . sin P
18 = 36 . sin P
sin P = ½
P = 300
Maka tan P = tan 300 =
Jawaban E
- 36
- 23
- 56
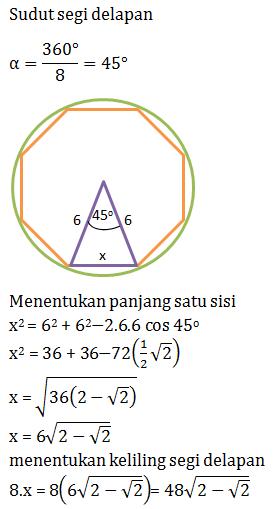
PEMBAHASAN :
Rumus untuk luas segi-n dengan panjang jari-jari lingkaran luarnya r sebagai berikut:
Jawaban C
cm
- 5 cm
cm
cm
- 6 cm
PEMBAHASAN :
Dapat menggunakan rumus dengan aturan kosinus, yaitu:
p2 = q2 + r2 – 2pq . cos P
q = 10 cm
r = 6 cm
∠P = 600
p2 = 102 + 62 – 2.10.6. cos 600
= 136 – 120 . ½
= 76
P = cm =
cm
Jawaban A
PEMBAHASAN :
Jawaban D
PEMBAHASAN :
Sedangkan ∠PQO dapat dihitung sebagai berikut:
Maka x = 750 + 750 = 1500
Sehingga cos x + tan x = cos 1500 + tan 1500
Jawaban A
- 0
- 1
- -1
- ½
- ∼
PEMBAHASAN :
Diketahui:
∠ ABC , ⊥B
sin (B + A) = x
sin B . cos A + cos B . sin A = x
1 . cos A + 0 = x
cos A = x
sin C = sin [1800 – (B + A)]
= sin (B + A)
= x
Maka cos A – sin C = x – x = 0
Jawaban A
dan
dan
dan
dan
dan
PEMBAHASAN :
6 cos2 x – cos x – 1 = 0 , – ½ π < x < ½ π
(2 cos x – 1)(3 cos x + 1) = 0
cos x = ½ dan cos x = - ¹/3
cos x = ½ → sin x =
cos x = → sin x =
Jawaban B
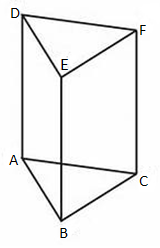
PEMBAHASAN :
ΔABC
Panjang AB = 6 cm
Panjang AC = 8 cm
∠BAC = 600
Dapat menggunakan rumus dengan aturan kosinus, yaitu:
BC2 = AC2 + AB2 – 2.AC.AB.cos ∠BAC
= 82 + 62 – 2.8.6.cos 600
= 64 + 36 – 48
= 52
BC = 2√13
Maka cos B dapat dihitung sebagai berikut:
Jawaban E
PEMBAHASAN :
ΔLMN
Tinggi segitiga pada garis NT
∠LMN = 600
Panjang LN = a
Panjang LT = a
Perhatikan ΔLNT dengan siku-siku di T sebagai berikut:
Catatan:
Menentukan panjang sisi segitiga dengan sudut yaitu:
300 : 600 : 900 → 1 : ![]() : 2
: 2
Maka Panjang MN dapat dihitung sebagai berikut:
Jawaban D
- {x|100 < x < 700}
- {x|150 < x < 750}
- {x|150 < x < 750}
- {x|250 < x < 850}
- {x|150 < x < 750}
PEMBAHASAN :
sin 2x > ½ , 00 ≤ x ≤ 1800
Menentukan nilai x yang memenuhi dari sin 2x > ½ dengan 00 ≤ x ≤ 1800
Perhatikan gambar di bawah ini!
sin 2x > ½
300 < 2x < 1500 → 150 < x < 750
Maka himpunan penyelesaiannya adalah
{x|150 < x < 750}
Jawaban C
PEMBAHASAN :
Ilustrasikan dalam gambar di bawah ini!
Kapal bergerak dari titik P ke titik Q. Kemudian bergerak 30o ke titik R. Jarak kapal terhadap posisi saat kapal berangkat adalah PR
Berlaku aturan kosinus sebagai berikut:
(PR)2 = (PQ)2 + (QR)2 – 2.(PQ).(QR) cos ∠PQR
= 202 + 402 – 2.20.40. cos 1200
= 400 +1600 – 1600. – ½
= 2800
PR =
Jawaban A
PEMBAHASAN :
900 < x < 1800 → kuadran II
tan x = a , karena berada dikuadran II a bernilai negatif sehingga menjadi tan x = - a.
Juga di kuadran II sin bernilai positif dan cos bernilai negatif.
Maka:
Jawaban D
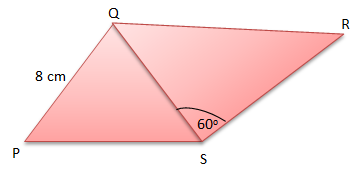
PEMBAHASAN :
Diketahui:
ΔPQR dengan S adalah titik tengah PR
Panjang QR = p
Panjang PR = q
Panjang PQ = r
Panjang QS = s
Perhatikan ΔQSR:
Perhatikan ΔPQS:
Jawaban E
PEMBAHASAN :
Diketahui:
PQR = segitiga lancip
Maka sin R = sin (P + Q)
Sin R = sin P . cos Q + cos P . sin Q
Jawaban B
PEMBAHASAN :
Jawaban A
PEMBAHASAN :
∠P dan ∠Q segitiga lancip
Jawaban E
PEMBAHASAN :
Jawaban C
PEMBAHASAN :
Jawaban D
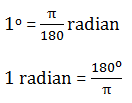





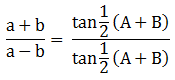

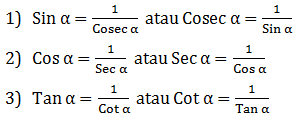
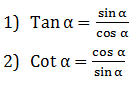
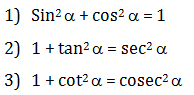
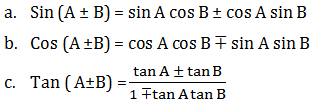
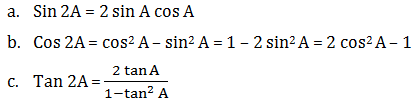


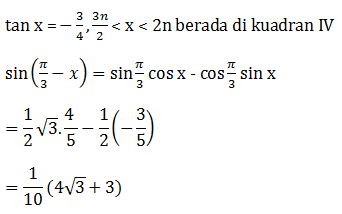

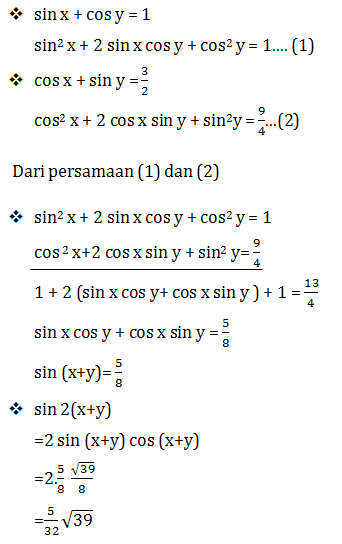
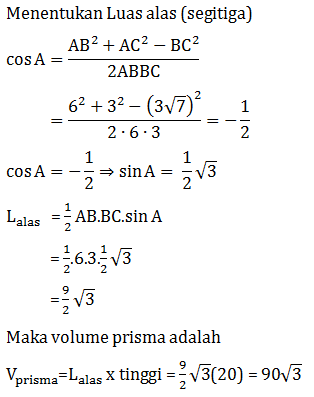




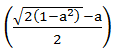
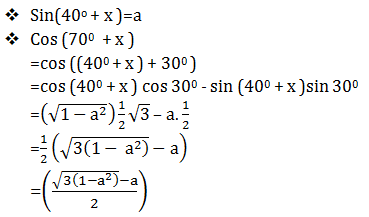
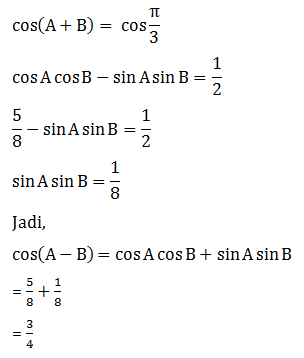
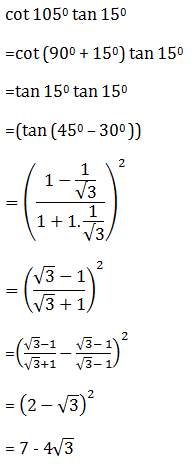
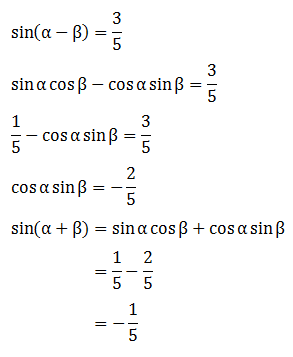


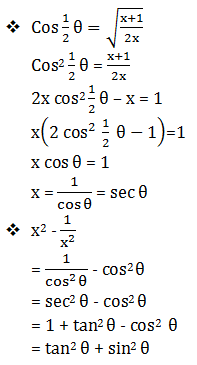
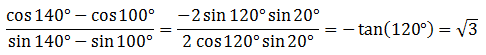


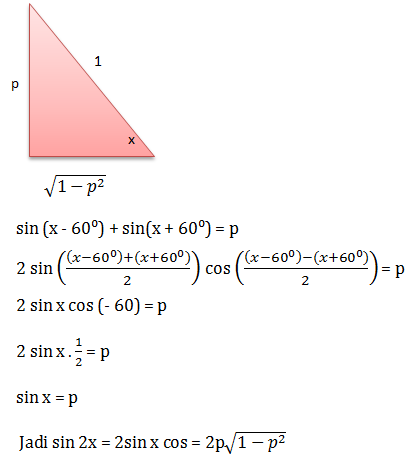
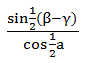
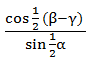

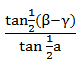
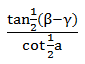
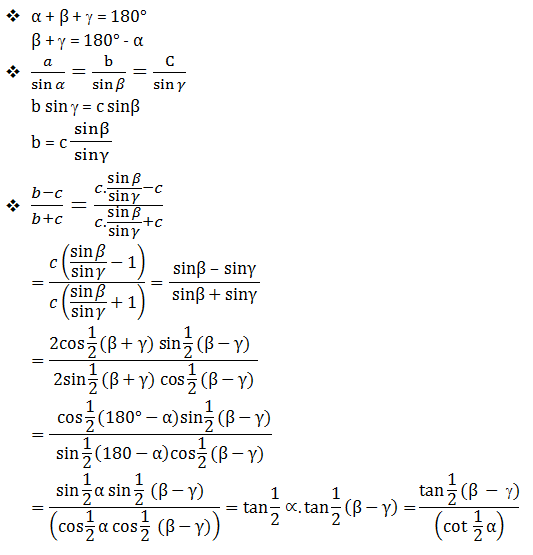

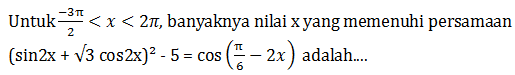




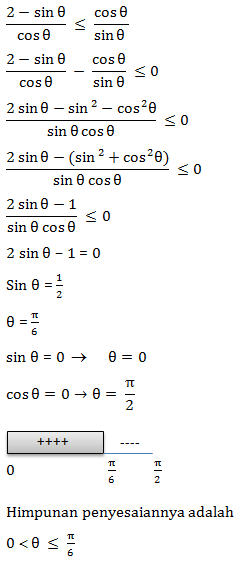

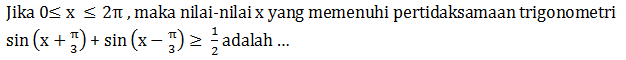
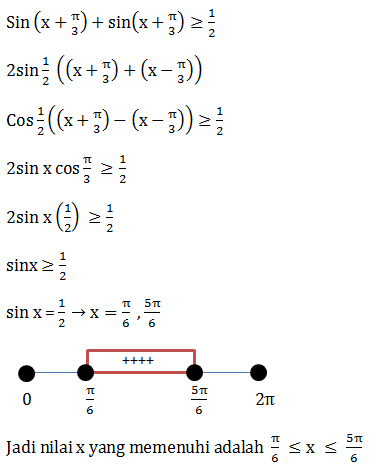

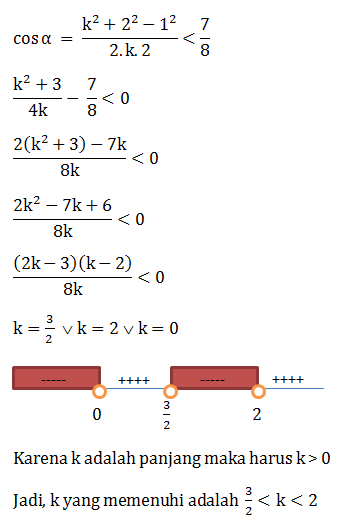

izin download
Izin download