Soal UTBK Matematika Tahun 2019 Dan Pembahasannya Part II
, maka nilai m adalah…
- -1 < m < 1
- -2 < m < 2
PEMBAHASAN :
………kalikan 8
⇒ 2x2 + + (m2x2 + 8mx + 16) = 8
⇒ (2+m2)x2 + 8mx + 8 = 0
Karena tak berpotongan, berarti D < 0 :
(8m)2 – 4.(2 + m2).8 < 0
⇒ 64m2 – 64 – 32m2 < 0
⇒ 32m2 – 64 < 0 ………..dibagi dengan 32
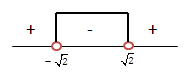
⇒ m2 – 2 < 0
Jawaban D
dan B + C = 
. Jika A adalah matriks berukuran 2 x 2 sehingga AB + AC = 
, maka determinan dari AB adalah….- 4
- 2
- 1
- -1
- -2
PEMBAHASAN :
Misalkan: 
Mencari a,b,c dan d
2a – 3b = 4 |x 1| 2a – 3b = 4
a + b = 2 |x 2|2a + 2b = 4 –
……………………………..-5b = o,
maka b = o dan a = 2
2c – 3d = -3 |x 1| 2c – 3d = -3
c + d = 1 |x 2| 2c + 2d = 2 –
…………………………….-5d = -5,
maka d = 1 dan c = 0
∴ det (A.B) = det A. det B = 2.2 = 4
Jawaban A
LIHAT JUGA : Soal UTBK I Matematika 2019 Part I
, maka banyaknya bola berwarna biru adalah…- 1
- 3
- 5
- 7
- 9
PEMBAHASAN :
P(2M) + P (1M dan 1B) = 
Dimana:
mC1 = m
10-mC1 = 10 – m
Maka
……………………..kalikan 90
⇒ m2 – m + 20m – 2m2 = 18
⇒ -m2 + 19 m – 18 = 0 ……………………kalikan (-1)
⇒ m2 – 19 m + 18 = 0
⇒ (m – 1)(m – 18) = 0
⇒ m1 = 1 atau m2 = 18 (tak memenuhi syarat, junlah bola = 10)
∴ bola biru = 10 – 1 = 9
Jawaban E
Diberikan 7 data, setelah diurutkan, sebagai berikut: a, a+1, a+1, 7, b, b, 9. Jika rata-rata data tersebut 7 dan simpangan rata-ratanya
, maka a + b = ….- 12
- 13
- 14
- 15
- 16
PEMBAHASAN :
⇒3a + 2b + 18 = 49
⇒ 3a + 2b = 31
Dengan melihat a < 7 dan b > 7, dan mencoba ‘memasukkan’ nilai a = 0, 1, 2, 3, 4, 5, dan b = 7,8,
akan didapat nilai a dan b yang tepat masing-masing adalah 5 dan 8, yang memenuhi 3a + 2b = 31
∴ a + b = 5 + 8 = 13
Jawaban B
- α = -β + 45o
- α = -β + 60o
- α = -β + 90o
- α = -β + 120o
- α = -β + 180o
PEMBAHASAN :
x = sin α + sin β ⇒ x2 = sin2 α + 2sin α. sin β + sin2 β
y = cos α – cos β ⇒ y2 + = cos2 α – 2cos α. cos β + cos2 β +
………………………..x2 + y2 = 1-2(cos α. cos β – sin α. sin β) + 1
⇒ x2 + y2 = 2 – 2 cos (α + β)
∴ Nilai terbesar x2 + y2 terjadi saat:
cos (α + β) = -1
⇒ cos (α + β) = cos 180o
⇒ α + β = 180o
⇒ α = -β + 180o
Jawaban E
PEMBAHASAN :
Joni:
Mo = A
M3 = B
⇒ Mo. (1 + b)3 = B
⇒ A. (1 + b)3 = B
Citra:
Mo = x
M3 > B
⇒ Mo. (1 + b)6 > B
⇒ x. ((1 + b)3)2 > B
Dimana 
, artinya salah satu nilai x yang memenuhi adalah 
Jawaban A
, maka nilai 
adalah ….- 1
- 2
- 3
- 4
- 6
PEMBAHASAN :
⇒ x + 6 = -ay + b
Dimana:
berarti:
b-6 = 0 ⇒ b = 6
Jawaban B
PEMBAHASAN :
- Δ BDD’ ∼ Δ ABC : DD’ =
AC = a - BD’ = BC = b
- CD’ = BC – BD’ = b – b =
b
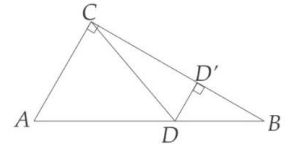
∴ Luas CDD’ = ½ x alas x tinggi = ½ x DD’ x CD’ = ½ x 
a x 
b = 
ab
Jawaban D
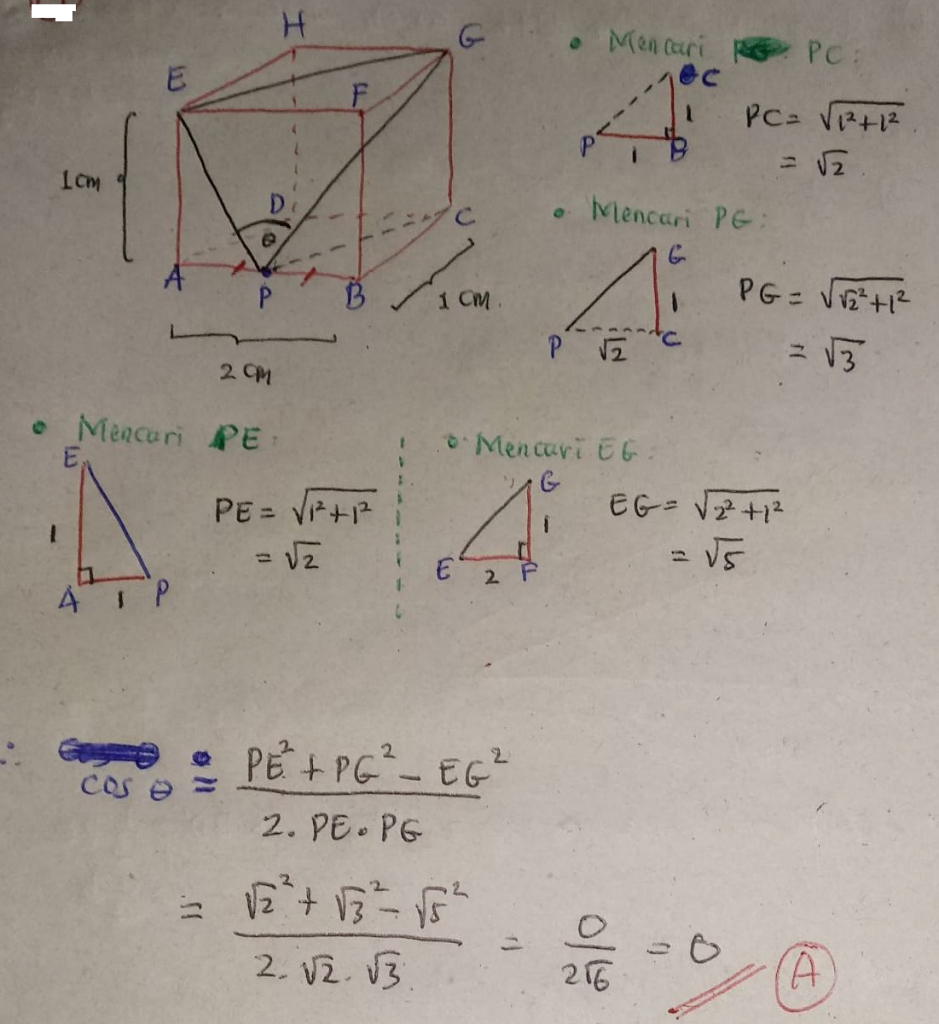
Misalkan balok ABCD.EFGH dengan AB = 2 cm, BC = 1 cm, dan AE = 1 cm. Jika P adalah titik tengah AB dan θ adalah ∠EPG, maka cos θ adalah….
- 0
- 1
PEMBAHASAN :
Jawaban A
PEMBAHASAN :
cos 2x + cos 2y = 
⇒ (1 – 2 sin2 x) + (1 – 2 sin2 y) =
⇒ 2 – 2 sin2 x – 2 (2 sin x)2 =
⇒ -10. sin2 x = 
⇒ sin2 x = 
⇒ sin x =
Sin y = 2. sin x
⇒ sin y = 2.
⇒ sin y = 
Jawaban B