Soal UTBK TKA Saintek Kimia 2021
Soal No.1
Jika pada ΔABC diketahui sin A = ½ , tan B = 2, dan |AC| = 4, |AB| = …
Jika pada ΔABC diketahui sin A = ½ , tan B = 2, dan |AC| = 4, |AB| = …
- 2 +
- 2 +
- 1 + 2
- 1 + 2
- 1 +
Soal No.2
Jika system persamaan 
memiliki penyelesaian (a,b), maka nilai 2a + b yang mungkin adalah …
memiliki penyelesaian (a,b), maka nilai 2a + b yang mungkin adalah …- 4
- 3
- 2
- 1
- 0
Soal No.3
Himpunan penyelesaian pertidaksamaan (x2 – 2)2 – 6 > |x2 – 2| adalah …
Himpunan penyelesaian pertidaksamaan (x2 – 2)2 – 6 > |x2 – 2| adalah …
- {x : x < – atau x > }
- {x : 0 ≤ x < }
- {x : – < x ≤ 0}
- {x : – < x < }
- {x : – 5 < x < 5}
atau x > Soal No.4
Jika a log c = 9 dan b log c = 3, maka a log ab = …
Jika a log c = 9 dan b log c = 3, maka a log ab = …
- 9
- 6
- 4
- 3
- 2
Soal No.5
Jika garis – 2x + y = 1 dicerminkan terhadap garis x =2 menghasilkan garis ax + y = b, maka 3a – b = …
Jika garis – 2x + y = 1 dicerminkan terhadap garis x =2 menghasilkan garis ax + y = b, maka 3a – b = …
- – 4
- – 3
- – 2
- 1
- 3
Soal No.6
Diberikan barisan aritmetika x1, x2, x3, … jika x1 + x2 + x3 = 2 dan x4 + x5 + x6 = 8, maka x1 + x2 + … + x15 = …
Diberikan barisan aritmetika x1, x2, x3, … jika x1 + x2 + x3 = 2 dan x4 + x5 + x6 = 8, maka x1 + x2 + … + x15 = …
- 64
- 70
- 76
- 80
- 84
Soal No.7
Jika
,maka 2a – 12b = …
Jika
,maka 2a – 12b = …- -6
- -4
- -3
- -2
- 0
Soal No.8
Diberikan fungsi f dengan f(x) ≥ 0 untuk setiap x ∈ R. Jika
dan daerah {(x,y):0 ≤ y ≤ f(x), 1 ≤ x ≤ 4} memiliki luas t, maka luas {(x,y):0 ≤ y ≤ f(x), 1 ≤ x ≤ 2} adalah …
Diberikan fungsi f dengan f(x) ≥ 0 untuk setiap x ∈ R. Jika
dan daerah {(x,y):0 ≤ y ≤ f(x), 1 ≤ x ≤ 4} memiliki luas t, maka luas {(x,y):0 ≤ y ≤ f(x), 1 ≤ x ≤ 2} adalah …- – s – t
- – s + t
- – 2s – t
- – 2s + t
- s + t
Soal No.9
Diberikan fungsi f dan g dengan g(x) = (ax + f(x + 1))2 dan a > 0. Jika g’(1) = 24, f’(2) = – 1, dan f(2) = 3, maka 3a + 1 = …
Diberikan fungsi f dan g dengan g(x) = (ax + f(x + 1))2 dan a > 0. Jika g’(1) = 24, f’(2) = – 1, dan f(2) = 3, maka 3a + 1 = …
- 4
- 5
- 7
- 10
- 13
Soal No.10
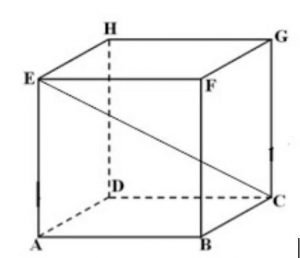
Diketahui panjang rusuk kubus ABCD.EFGH adalah 3. Jika P adalah titik pada EC dengan |EP| : |PC| = 1 : 5, maka jarak P ke H adalah …
Soal No.11
Andi menabung sejumlah uang dengan bunga majemuk. Jika pada akhir tahun ke-15 uang Andi menjadi 3 juta rupiah dan pada akhir tahun ke-30 uang Andi menjadi 9 juta rupiah, maka uang yang Andi tabungkan pada tahun pertama adalah … rupiah.
Andi menabung sejumlah uang dengan bunga majemuk. Jika pada akhir tahun ke-15 uang Andi menjadi 3 juta rupiah dan pada akhir tahun ke-30 uang Andi menjadi 9 juta rupiah, maka uang yang Andi tabungkan pada tahun pertama adalah … rupiah.
- 0,5 juta
- 1 juta
- 1,5 juta
- 2 juta
- 2,5 juta
Soal No.12
Diberikan fungsi
. Jika f-1 (a + 2) = 0, maka a2 + 1 = …
Diberikan fungsi
. Jika f-1 (a + 2) = 0, maka a2 + 1 = …- 1
- 2
- 3
- 4
- 5
Soal No.13
Diberikan vektor – vektor
dan dengan = 4
– 2
+ 4
. Jika 
vektor proyeksi pada dengan || = 2 dan 
vektor proyeksi pada dengan || = 4, maka || = …
Diberikan vektor – vektor
dan 
dengan = 4
– 2
+ 4
. Jika 
vektor proyeksi pada dengan || = 2 dan 
vektor proyeksi pada dengan || = 4, maka || = …- 3
- 4
Soal No.14
Jika luas daerah di kuadran I yang terletak di atas kurva y = (x – 1)2 dan di bawah garis y = 1 + 4m – 2mx dengan m > 0 adalah 40/3 , maka m =…
Jika luas daerah di kuadran I yang terletak di atas kurva y = (x – 1)2 dan di bawah garis y = 1 + 4m – 2mx dengan m > 0 adalah 40/3 , maka m =…
- 2
- 3
- 4
- 5
- 6
Izin .. ambil soal untuk saya bahas ya Pak,
terimakasih