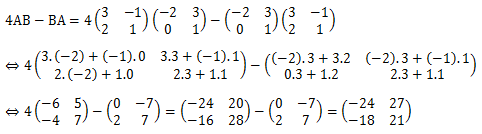Contoh Soal & Pembahasan Matriks Bagian II
PEMBAHASAN :
Diketahui:
P + Q = C’
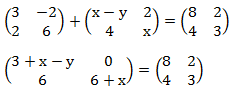
Maka diperoleh:
- 6 + x = 3, maka x = -3
- 3 + x - y = 8, maka 3 + (-3) – y = 8
y = -8
Sehingga diperoleh x + y = -3 + (-8) = -11
DOWNLOAD KUMPULAN SOAL CONTOH SOAL MATRIKS SMA BAGIAN II DALAM BENTUK PDF KLIK DISINI
PEMBAHASAN :
![]()
Karena Matris (P-kQ) singular maka determinan matriks tersebut bernilai 0
|P - k.Q|= 0
Maka :
![]()
(k+1)k = 12
k2 + k = 12
k2 + k - 12 = 0
(k+4)(k-3) = 0
Maka nilai yang memenuhi adalah k = -4 dan k = 3
Diketahui matriks P =
 , jika nilai deteminannya adalah 4, Tentukan nilai -2x + y - z = 0
, jika nilai deteminannya adalah 4, Tentukan nilai -2x + y - z = 0
PEMBAHASAN :
Menentukan matriks PQ
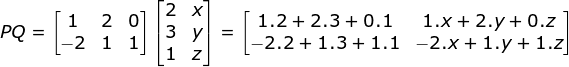
![]()
Diketahui determinannya = 4, maka:
![]()
8(-2x+y+z)-0=4
Maka
-2x+y+z = 0,5
PEMBAHASAN :
Menentukan PQ
![]()
![]()
Menentukan (PQ)-1
![]()
PEMBAHASAN :
Jika
Maka matriks X
X = P-1.Q
![]()
![]()
![]()
PEMBAHASAN :
Menentukan P-1 (P-1 = invers matriks P)
P = ![]()
P-1 = ![]()
Menentukan nilai X
P-1.Q = ![]()
P-1.Q = R
![]()
Maka:
3x - 10 = 2
3x = 10 + 2 = 12
x = 4
PEMBAHASAN :
Jika:
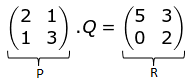
Sehingga P. Q = R
Menentukan salah satu determinan bisa menggunakan rumusan
|P|.|Q| = |R|
(2.3-1.1). |Q| = (5.2-0.3)
(5).|Q| = (10)
|Q| = 2
PEMBAHASAN :
Sistem persamaan tersebut diubah menjadi
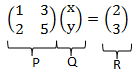
PQ = R
Q = P-1.R
Menentukan P-1
P-1 = ![]()
Maka:
![]()
x = -1 dan y = 1, sehingga:
2x - 5y = 2(-1) - 5(1) = -7
PEMBAHASAN :
Diketahui:
Translasi dengan M1 = ![]()
Dilatasi pusat O dan faktor skala 2, M2 = ![]()
Menentukan hasil transformasi
![]()
![]()
![]()
![]()
Sehingga nilai x dan y
x’ = 6+2x
![]()
y’ = -8 + 2y
![]()
Maka hasil transformasinya adalah
![]()
⇔ 3(x’ - 6) + 2(y’ + 8) = 12
⇔ 3x’ + 2y’ = 14
⇔ 3x + 2y = 14
DOWNLOAD KUMPULAN SOAL CONTOH SOAL MATRIKS SMA BAGIAN II DALAM BENTUK PDF KLIK DISINI
 tanya-tanya.com Jika bisa gratis kenapa harus bayar
tanya-tanya.com Jika bisa gratis kenapa harus bayar