Rangkuman Materi Eksponen & Logaritma Kelas X

Eksponen

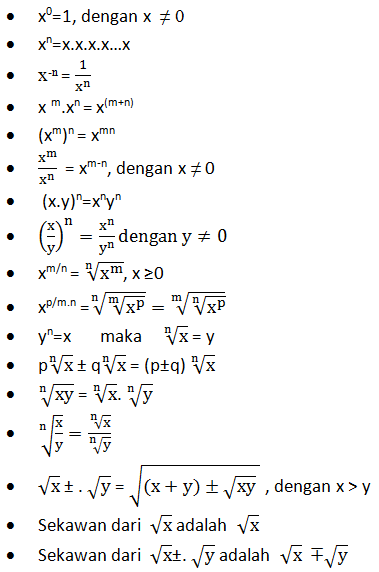
Logaritma

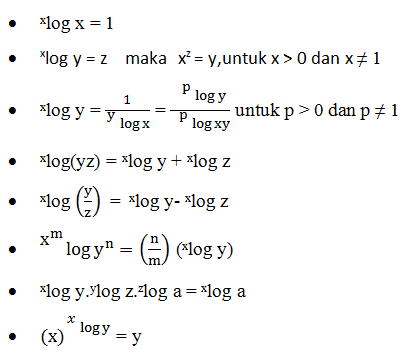
Contoh Soal Eksponen Kelas 10 dan Logaritma Berikut Pembahasan dan Jawaban

Soal No.11 (UM UGM 2008)

1. 
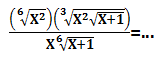
2. x
3. 1
4. 
5. 

PEMBAHASAN :

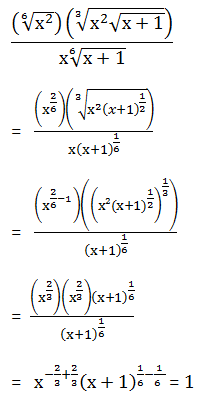
Jawaban : C

Soal No.12 (UM UGM 2009)

1. 3/5
2. 5/3
3. 1+ ^ablog ab²
4. 1 + ^ablog a²b
5. 

PEMBAHASAN :

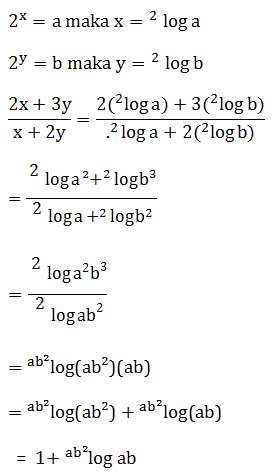
Jawaban : E

Soal No.13 (SNMPTN 2008 DASAR)
Dalam bentuk pangkat rasional

PEMBAHASAN :

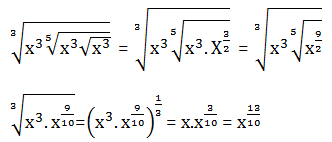
Jawaban : C

Soal No.14 (UN 2009)
Akar-akar persamaan 9^x -12.3^x + 27 = 0 adalah α dan β. Nilai αβ = …..

1. -3
2. -2
3. 1
4. 2
5. 3

PEMBAHASAN :
9^x − 12.3^x + 27 = 0
(3^x)² − 12.3^x + 27 = 0
Jika dimisalkan 3^x = a, maka:
a² − 12a + 27 = 0
(a-9)(a-3) = 0
a − 9 = 0
a = 9
3^x = a = 9
3^x = 3²
x = 2 =α
dan
a − 3 = 0
a = 3
3^x = a = 3
3^x = 3¹
x = 1 = β
Maka:
αβ = 2.1 = 2
Jawaban : D

Soal No.15 (UN 2009)
Diketahui . Nilai x yang memenuhi persamaan itu adalah…..

1. 
2. 
3. 4
4. 
5. 

PEMBAHASAN :






4x – 16 = 6
4x = 22

Jawaban : D

Soal No.16 (UN 2008)
Himpunan penyelesaian dari pertidaksamaan eksponen 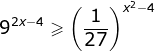adalah….

PEMBAHASAN :

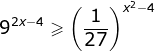
(3²)^2x-4 ≥ (3^-3)^x2-4
4x – 8 ≥ -3x² + 12
3x² + 4x – 20 ≥ 0
(3x + 10)(x − 2) ≥ 0
dan x = 2

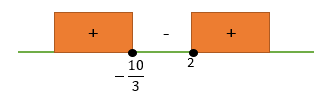
HP =

Jawaban : C

Soal No.17 (UN 2014)
Penyelesaian dari 3^2x+3 – 84.3^x + 9 ≥ 0 adalah….

1. -1 ≤ x ≤ 2
2. -2 ≤ x ≤ 1
3. x ≤ -2 atau x ≥ -1
4. x ≤ -2 atau x ≥ 1
5. x ≤ 1 atau x ≥ 2

PEMBAHASAN :
3^2x+3 – 84.3^x + 9 ≥ 0
(3^x)².3³ – 84. 3^x + 9 ≥ 0
Jika dimisalkan 3^x = a
27a² + 84a + 9 ≥ 0
9a² − 28a + 3 ≥ 0
(9a − 1)(a − 3) ≥ 0
a = 1/9 dan a = 3

Jika a = 1/9
3^x = a = 1/9
3^x = (1/3)²
x = -2

Jika a = 3
3^x = a = 3
3^x = 3¹
x = 1

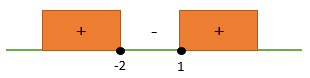
HP = x ≤ -2 atau x ≥ 1
Jawaban : D

Soal No.18 (UN 2014)
Himpunan penyelesaian dari 3^2x − 6.3^x < 27 adalah….

1. {x | x < -3, x ∈ R}
2. {x | x < -2, x ∈ R}
3. {x | x < 2, x ∈ R}
4. {x | x > 2, x ∈ R}
5. {x | x > 3, x ∈ R}

PEMBAHASAN :
3^2x − 6.3^x < 27
3^2x − 6.3^x − 27 < 0
Jika dimisalkan 3^x = a
a² – 6a – 27 < 0
(a − 9)(a + 3) < 0
a = 9 dan a = -3

Jika a = 9
3^x = a = 9
3^x = (3)²
x = 2

Jika a = -3
3^x = a = -3
3^x = -3
x = tidak memenuhi

Maka pilihannya tinggal x < 2 atau x > 2
Jika disubstitusikan nilai = 1 (x <2)ke pertidaksamaan 3^2x − 6.3^x < 27
3^2.1 − 6.3¹ < 27
9 – 18 < 27
-9 < 27 (memenuhi)

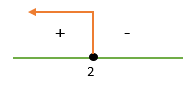
HP = x < 2
Jawaban : C

Soal No.19 (UN 2014)
Penyelesaian pertidaksamaan ³log x . ^1-2xlog 9 > 2 − ^1-2xlog 9 adalah….

1. 0 < x <
2. 0 < x <
3. 0 < x <
4. < x < 
5.  < x <

PEMBAHASAN :
Syarat terpenuhi:

• x > 0
• 1 – 2x > 0, maka x < ½
• ³log x . ^1-2xlog 9 > 2 − ^1-2xlog 9
  ^1-2xlog 3² . ³log x > ^1-2xlog (1-2x)² − ^1-2xlog 9
  
  
  
  
  5x² + 4x − 1 > 0
  (5x − 1)(x + 1) > 0
  5x -1 = 0
  x = 
  atau
  x + 1 = 0
  x = -1
  Maka garis bilangannya
  
  karena x > o dan x < ½ maka:
  
  Sehingga penyelesaiannya
  < x < 

Jawaban : D

Soal No.20 (UN 2013)
Penyelesaian dari pertidaksamaan ²⁵log (x-3) + ²⁵log (x + 1) ≤ ½ adalah….

1. -2 < x < 4
2. -3 < x < 4
3. x < -1 atau x > 3
4. 3 < x ≤ 4
5. 1 < x < 2 atau 3 < x < 4

PEMBAHASAN :
Syarat terpenuhi:

• x − 3 > 0, maka x > 3
• x + 1 > 0, maka x > -1
• ²⁵log (x − 3) + ²⁵log (x + 1) ≤ ½
  ²⁵log ((x − 3)(x + 1)) ≤ ²⁵log 25½
  x² − 2x − 3 ≤ 5
  x² − 2x − 8 ≤ 0
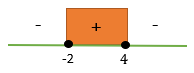
  (x − 4)(x + 2) ≤ 0
  x − 4 = 0
  x = 4
  atau
  x + 2 = 0
  x = -2
  Maka garis bilangannya
  
  karena x > 3 dan x > -1 maka:
  
  Sehingga penyelesaiannya
  3 < x ≤ 4

Jawaban : D