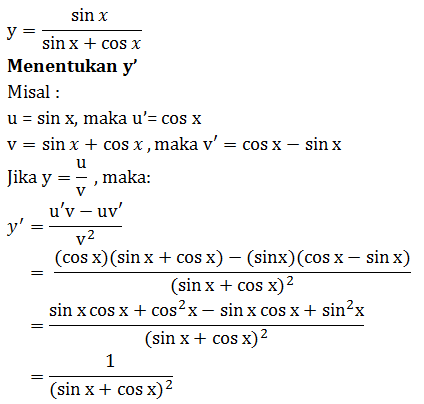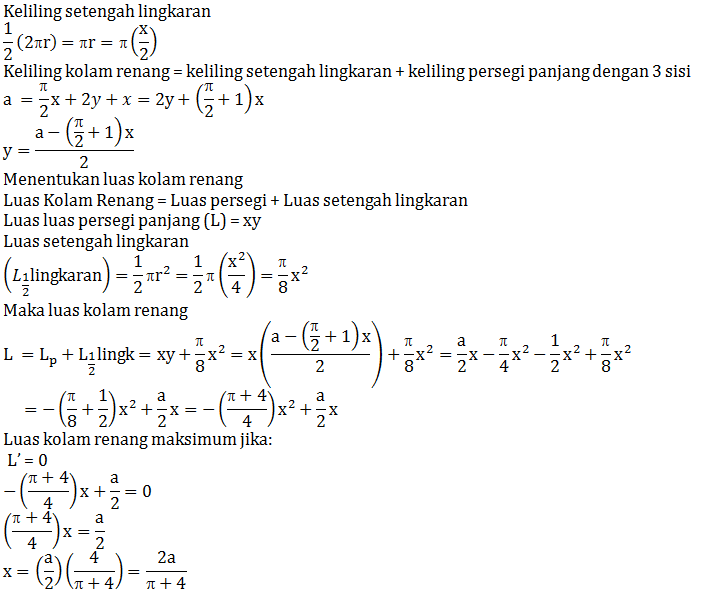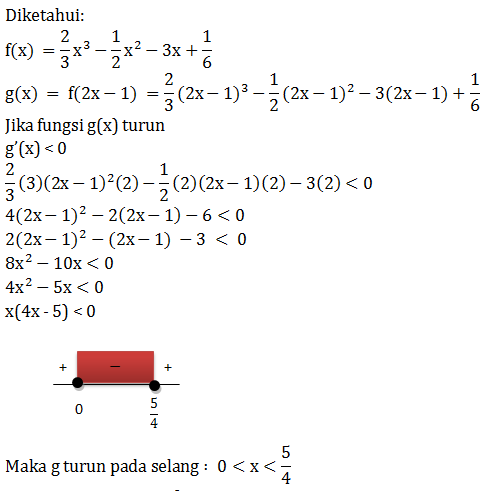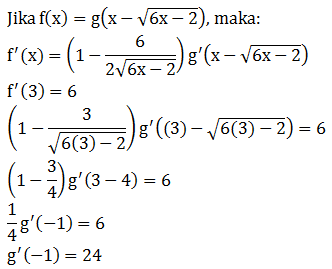Rangkuman Materi Turunan Kelas XI/11

Turunan Pertama

Turunan pertama dari suatu fungsi f(x) adalah:

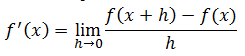
Jika f(x) = xⁿ, maka f ’(x) = nx^n-1, dengan n ∈ R
Jika f(x) = axⁿ, maka f ’(x) = anx^n-1, dengan a konstan dan n ∈ R
Rumus turunan fungsi aljabar:
Jika y = c maka y’= 0
Jika y = u + v, maka y’ = u’ + v’
Jika y = u – v, maka y’ = u’ – v’
Jika y = k u, maka y’ = k u’
Jika y = u v, maka y’ = u’v + uv’
Jika y = , maka y’ =
Jika y = uⁿ, maka y’ = n u^n-1
Jika y = f(u), maka y’ = f ’(u).u’
Jika y = (g o h)(x) = g(h(x)), maka y’ = g’(h(x)).h’(x)
Jika y = In x, maka y ’=

Turunan Fungsi Trigonometri

1. Jika y = sin x, maka y’= cos x
2. Jika y = cos x, maka y’ = -sin x
3. Jika y = tan x, maka y’= sec²x
4. Jika y = cot x , maka y’= -cosec²x
5. Jika y = sec x , maka y’ = sec x tan x
6. Jika y = cosec x , maka y’ =-cosec x cot x

Persamaan Garis Singgung

Jika kurva y = f(x), maka gradien garis singgung kurva tersebut di x = a adalah:

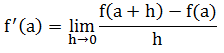
Persamaan garis singgung dari kurva y = f(x) melalui (x₁, y­₁) adalah:
(y – y₁) = m(x – x₁) atau (y – y₁) = f ‘(x₁) (x – x₁)

Fungsi Naik Turun

Fungsi dikatakan naik jika f’ (x) > 0
Fungsi dikatakan turun jika f’ (x) < 0

Stasioner

Fungsi f(x) dikatakan stasioner jika f ’ (x) = 0
Jenis titik stasioner ada 3 yaitu:

1. titik balik maksimum, jika f “(x) < 0
2. titik balik minimum, jika f ”(x) > 0
3. titik belok horizontal, jika f “(x) = 0

Turunan Kedua

Turunan kedua dari suatu fungsi y = f(x) adalah turunan dari turunan pertama dan diberi lambang:

Contoh Soal & Pembahasan Turunan Kelas XI/11

Diketahui f(0)=1 dan f’(0)=2. Jika g(x) = , maka g’(0)=…

1. -12
2. -6
3. 6
4. 8
5. 12

PEMBAHASAN :
g(x)= =(2(f(x) – 1)^-3
g'(x)=(-3)(2(f(x) – 1)^-4.(2)(f ‘(x)) = (-6)(f ‘(x))(2(f(0)- 1)^-4
g’ (0)=(-6)(f’ (0))(2(f(0) – 1)^-4 = (-6)(2)(2(1) – 1)^-4 = -12
Jawaban : A

Soal No.2 (UN 2007)

Turunan pertama dari f (x) = adalah f ’(x) =…

PEMBAHASAN :

Jawaban : E

Diketahui

1. f(0) = 1
2. f’(-1) tidak ada
3. f turun pada x > 0
4. f(x) diskontinu di titik x =-1
5. f(x) kontinu di titik x=5

PEMBAHASAN :

Jawaban : A

Turunan pertama dari y = adalah y’ =…

PEMBAHASAN :

Jawaban : B

1. b² – 4ac < 0 dan a ˃ 0
2. b² – 4ac < 0 dan a ˂ 0
3. b² – 3ac > 0 dan a ˂ 0
4. b² – 3ac < 0 dan a˃ 0
5. b² – 3ac < 0 dan a˂ 0

PEMBAHASAN :
Jika f(x) = ax³ – x² + cx + 12, maka f’(x) = 3ax² – 2bx + c
fungsi f(x) akan naik jika:
f’(x) > 0
3ax² – 2bx + c > 0
Agar fungsi bernilai positif :

• koefisien x² > 0
  3a > 0
  a > 0

• D < 0
  (-2b)² – 4(3a)(c) < 0
  4b² – 12ac < 0
  b² – 3ac < 0

Jawaban : D

Di ketahui f(x) = . Jika f(x) menyatakan turunan pertama f(x) maka f(0) + 2 f ’(0) = …

1. -10
2. -9
3. -7
4. -5
5. -3

PEMBAHASAN :

Jawaban : B

PEMBAHASAN :

Jawaban : E

PEMBAHASAN :

Jawaban : D

1. -6
2. -4
3. -2
4. 2
5. 4

PEMBAHASAN :
Jika f(x) = mx³ + 2x² – nx + 5 maka f ’(x) = 3mx² + 4x – n
Diketahui
f(1) = 0
3m(1)² + 4(1) – n = 0
3m – n = -4
Jawaban : B

1. 1 < x < 3
2. -1 < x < 3
3. -3 < x < 1
4. x < -3 atau x > 1
5. x < -3 atau x > 3

PEMBAHASAN :
Jika f(x) = x³ – 3x² – 9x – 7
maka f ‘(x) = 3x² + 6x -9
Fungsi akan turun jika f ‘(x) < 0, maka:
3x² + 6x -9 < 0
x²⁺ + 2x – 3 < 0
(x+3)(x-1) < 0

Maka fungsi f(x) turun saat -3 < x < 1
Jawaban : C

Jika (a,b) adalah titik minimum grafik fungsi f(x) = 7 – maka nilai a² + b² adalah …

1. 4
2. 5
3. 8
4. 10
5. 13

PEMBAHASAN :

Jawaban : A

Nilai minimum fungsi f(x) = x³ + x² – 3x + 1 pada intrerval 0 ≤ x ≤ 3 adalah …..

1. -1
2. 
3. 
4. 
5. 1

PEMBAHASAN :

Jawaban : B

Diberikan grafik fungsi f(x)=x+, x≠0 maka ….

1. Fungsi naik pada himpunan {x ∈R|x ˂ 0 atau x ˃2}
2. Fungsi turun pada himpunan {x ∈R|˂ 0 x ˃2}
3. Terjadi minimum lokal di titik (2,3)
4. Terjadi maksimum lokal di titik (0,0)

PEMBAHASAN :

Jawaban : A

Diketahui fungsi g(x)= x³ – A²x + 7, A konstanta. Jika f(x)= g(2x + 1) dan f turun pada ≤ x ≤ , nilai minimum relatif g adalah …

1. 
2. 
3. 2
4. 
5. 

PEMBAHASAN :

Jawaban : B

Diketahui = 2^y-3 maka nilai maksimum dari 3xy + 6x –3 adalah ….

1. 0
2. 
3. 
4. 
5. 5

PEMBAHASAN :

Jawaban : D

1. 100
2. 250
3. 500
4. 1250
5. 5000

PEMBAHASAN :
Diketahui:
q – 2p = 50
q = 50 + 2p
Jika dimisalkan, x = p² + q²
x = p² + (50+2p)² = p²+ 2500 + 200p + 4p² = 5p² + 200p+ 2500
Menentukan nilai minimum
x’ = 0
10p + 200 = 0
p= -20
q = 50 + 2(-20) = 10
Maka, p² + q² = (-20)² + (10)² = 500
Jawaban : C

Jika kurva y = (x²-a) (2x+b)³ turun pada interval -1 < x < maka nilai ab =…

1. -3
2. -2
3. 1
4. 2
5. 3

PEMBAHASAN :

Jawaban : D

Garis l menyinggung kurva y = 3 di titik yang berabsis 4. Titik potong garis l dengan sumbu x adalah …

PEMBAHASAN :

Jawaban : B

Diketahui f(x) = x³– x²-3x+. Jika g(x) = f(2x-1) maka g turun pada selang…

1. 
2. -1 ≤ x ≤
3. -1 ≤ x ≤ 1
4. -1 ≤ x ≤ 0
5. 0 ≤ x ≤ 1

PEMBAHASAN :

Jawaban : E

1. Rp. 149.000,00
2. Rp. 249.000,00
3. Rp. 391.000,00
4. Rp. 609.000,00
5. Rp. 757.000,00

PEMBAHASAN :
Diketahui:
Jumlah produk = x produk
Biaya B(x) =(9.000 +1.000 +10x²)
Harga jual H(x)= 5.000x
Fungsi laba :
L(x)=H(x) – B(x)
L(x) = 5.000x – (9.000 +1.000 +10x²) = -10x² + 4.000x – 9000
Menentukan laba maksimum
L ̍(x) = 0
-20x + 4000 = 0
x = 200
L(200) = -10(200)² + 4000 (200) – 9000 = 391.000
Jawaban : C

Diketahui f(x) = g(x – ) Jika f ’(3) = 6 maka g’(-1)=…

1. 12
2. 16
3. 20
4. 24
5. 28

PEMBAHASAN :

Jawaban : D

1. \frac{1}{3}\sqrt{7} m
2. m
3. m
4. m
5. m

PEMBAHASAN :

Jawaban : D

1. 
2. 
3. 
4. (3,2)
5. 

PEMBAHASAN :

Jawaban : C

1. 2 m, 1 m, 2 m
2. 2 m, 2m, 1 m
3. 1 m, 2 m, 2 m
4. 4 m, 1 m, 1 m
5. 1 m, 1 m, 4 m

PEMBAHASAN :

Jawaban : B

Sebuah peluru ditembakkan vertikal ke atas. Jika tinggi h meter setelah t detik dirumuskan dengan h(t) = – t³ + t² + 2t + 10 maka tinggi maksimum yang dicapai peluru tersebut adalah….

1. 26
2. 18
3. 16
4. 14
5. 12

PEMBAHASAN :

Jawaban : C

1. 3 cm
2. 4 cm
3. 6 cm
4. 9 cm
5. 12 cm

PEMBAHASAN :

Jawaban : C

Turunan pertama dari fungsi adalah f'(x) = …

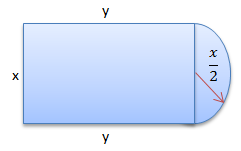
PEMBAHASAN :
Berlaku sebagai berikut:


Maka:



Jawaban : A

Turunan pertama dari fungsi adalah …

1. Y’ = cos 3x
2. Y’ = 3 cos 3x
3. Y’ = 6 cos 2 x
4. Y’ = cos 2x
5. Y’ = cos 6x

PEMBAHASAN :


Y’ = cos 6x
Jawaban : E

Jika y = 2 sin 3x – 3 cos 2x, maka

1. 2 sin 6x – 3 cos 6x
2. – 2 sin 3x + 2 cos 3x
3. 3 cos 6x – 2 sin 6x
4. 6 cos 3x +  6 sin 2x
5. – 6 cos 3x + 6 sin 2x

PEMBAHASAN :
y = 2 sin 3x – 3 cos 2x

Jawaban : D