DAFTAR ISI
Rangkuman Materi Bilangan Bulat Dan Pecahan Kelas 7 SMP
Bilangan Bulat
Terdiri dari bilangan negatif, bilangan nol (0) dan bilangan bulat positif. Jika dituliskan sebagai berikut
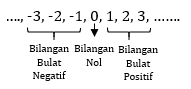
Jika dituliskan dalam bentuk garis bilangan, sebagai berikut:

Operasi Bilangan Bulat
Penjumlahan
Sifat Operasi Bilangan Bulat
- Komutatif (pertukaran)
Jika m dan n ∈ himpunan bilangan bulat, maka berlaku:
m + n = n + m
Contoh:
2 + 3 = 3 + 2 = 5
- Asosiatif (pengelompokan)
Jika m dan n ∈ himpunan bilangan bulat, maka berlaku
(m + n) + o = m + ( n + o)
Contoh:
(2 + 3) + 4 = 2 + (3 + 4) = 9
- Unsur identitas, jika m ∈ himpunan bilangan bulat, maka berlaku:
m + 0 = m
0 merupakan unsur identitas pada penjumlahan
- Memiliki invers atau lawan, jika m ∈ himpunan bilangan bulat, maka -m disebut invers atau lawan dari m, maka berlaku:
m + (-m) = (-m) + m = 0
Contoh:
4 + (-4) = (-4) + 4 = 0
- Tertutup, jika m dan n ∈ himpunan bilangan bulat, maka berlaku
m + n ∈ himpunan bilangan bulat
Pengurangan
Pada pengurangan bilangan bulat secara umum dapat dinyatakan sebagai berikut:
m – n = m+ (-n)
contohnya:
14 – 34 = -20
-12 – 32 = -44
Perkalian
Sifat-sifat operasi hitung perkalian sebagai berikut:
- Sifat tertutup
Apabila m dan n merupakan anggota himpunan bilangan bulat, maka m x n merupakan anggota himpunan bilangan bulat.
- Sifat komutatif (pertukaran)
Apabila m dan n merupakan anggota himpunan bilangan bulat, maka m x n = n x m.
- Sifat asosiatif (pengelompokkan)
Apabila m dan n merupakan anggota himpunan bilangan bulat, maka (m x n) x o = m x (n x o).
- Sifat distributif (penyebaran)
Berlaku sebagai berikut:
m x (n + o) =(m x n) + (m x o)
m x (n – o) = (m x n) – (m x o)
- Elemen/unsur identitas
Apabila m anggota himpunan bilangan bulat, maka m x 1 = m, 1 adalah unsur identitas.
Ketentuan pada perkalian bilangan bulat adalah:
- m x n = bilangan bulat positif
- m x (-n) = bilangan bulat negatif
- (-m) x n = bilangan bulat negatif
- (-m) x (-n) = bilangan bulat positif
Contohnya:
4 x (- 6) = – 24
(- 6) x (-7) = 42
Pembagian
Pembagian merupakan kebalikan dari operasi perkalian. Ketentuan pada operasi perkalian berlaku juga untuk operasi pembagian. Dengan catatan jika m merupakan anggota himpunan bilangan bulat, maka m : 0 = tidak terdefinisi dan 0 : m = 0.
Jika m, n, dan o adalah bilangan bulat, dengan n merupakan faktor m, dan n ≠ 0 maka berlaku:
m : n = o → m = n x o
contohnya:
50 : (- 2) = – 25
(- 80) : (- 16) = 5
Konsep Operasi Hitung Campuran pada Bilangan Bulat
Pada operasi hitung campuran bilangan bulat ada sifat-sifat yang harus dipenuhi, yaitu:
- Tanda operasi hitung dan tanda kurung harus diperhatikan dengan seksama.
- Pengerjaan bilangan yang ada dalam tanda kurung harus didahulukan/ diprioritaskan.
Apabila dalam suatu operasi hitung campuran bilangan bulat tidak terdapat tanda kurung, maka cara pengerjaannya sebagai berikut:
- Operasi hitung penjumlahan dan pengurangan sama-sama kuat sehingga pengerjaan yang sebelah kiri harus didahulukan.
- Operasi hitung perkalian dan pembagian sama-sama kuat sehingga pengerjaan yang sebelah kiri harus didahulukan.
- Operasi hitung perkalian dan pembagian sifatnya lebih kuat daripada penjumlahan dan pengurangan sehingga perkalian dan pembagian harus dikerjakan lebih dahulu daripada penjumlahan dan pengurangan.
Contohnya:
- 9 x 42 : 6 – 23
Penyelesaian:
9 x 42 : 6 – 23 = 9 x (42 : 6) – 23
= 9 x 7 – 23
= 40
- 450 : 9 – 10 + 4 x 6
Penyelesaian:
450 : 9 – 10 + 4 x 6 = (450 : 9) – 10 + (4 x 6)
= 50 – 10 +24
= 64
KPK dan FPB
KPK (kelipatan persekutuan terkecil)
Cara menentukan nilai KPK dari suatu bilangan adalah:
- Uraikan faktor pembentuk bilangan dari bilangan yang kita cari
- Pilih bilangan yang terkecil tapi bukan nol dari anggota himpunan kelipatan persekutuan
- Kemudian kalikan faktor-faktor prima yang berbeda dengan pangkat terbesar
Contohnya:
Tentukan KPK dari 8 dan 6
Penyelesaian cara I:
Bilangan dari kelipatan 8 : 0, 8, 16, 24, 32, 40, …
Bilangan dari kelipatan 6 : 0, 6, 12, 18, 24, 30, …
KPK dari 8 dan 6 adalah 24
Penyelesaian cara II:
Faktorisasi prima dari 8 = 23
Faktorisasi prima dari 6 = 21 x 3
Diperoleh 23 x 3 = 24
Maka, KPK dari 8 dan 6 adalah 24
FPB (faktor persekutuan terbesar)
Untuk menentukan FPB dari suatu bilangan dapat diperoleh dengan cara:
- Tentukan anggota bilangan himpunan faktor-faktor yang terbesar
- Kalikan faktor-faktor prima yang bernilai sama dengan pangkat terkecil
Contohnya:
Tentukan FPB dari 24 dan 36
Penyelesaian cara I:
Himpunan faktor-faktor dari 24: 1, 2, 3, 4, 6, 8, 12, 24
Himpunan faktor-faktor dari 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Maka FPB dari 24 dan 36 adalah 12
Penyelesaian cara II:
Faktorisasi prima dari 24 = 23 x 3
Faktorisasi prima dari 36 = 22 x 32
Diperoleh 22 x 3 = 12
Maka, FPB dari 24 dan 36 adalah 12
Pecahan
Bentuk pecahan adalah ![]() dengan n ≠ 0
dengan n ≠ 0
m = pembilang
n = penyebut
m dan n adalah ∈ himpunan bilangan bulat
Macam-macam pecahan
Persen
Contoh:
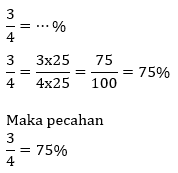
Pecahan sederhana
Contoh:

Maka bentuk paling sederhana dari pecahan ![]() adalah
adalah ![]()
Pecahan senilai
Contoh:
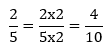
Maka pecahan ![]() senilai dengan pecahan
senilai dengan pecahan ![]()
Pecahan decimal
Contoh:
![]()
Maka bentuk desimal dari ![]() adalah 0,12
adalah 0,12
Pecahan campuran
Bentuk dari pecahan campuran dapat ditulis sebagai berikut:
![]() , o ≠ 0
, o ≠ 0
Contoh:
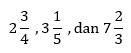
Operasi Hitung pada Pecahan
Perkalian pecahan
Sifat-sifat perkalian pecahan, yaitu:
- Komutatif

Dengan b ≠ 0 dan d ≠ 0
- Asosiatif

Dengan b, d, dan f ≠ 0
- Distributif

Dengan b, d, dan f ≠ 0
Pembagian pecahan
![]()
Catatan:
- a < b maka,

- a > b maka,

- 0 < a < b < c maka

Contoh:
![]()
Penjumlahan dan pengurangan
Penjumlahan dan pengurangan dapat langsung dilakukan jika penyebutnya bernilai sama (mencari KPK). Sifat-sifat untuk melakukan operasi hitung sebagai berikut:
- Komutatif
Berlaku:

b dan d ≠ 0
- Asosiatif
Berlaku:

b, d, dan f ≠ 0
Contoh:
Contoh Soal & Pembahasan Bilangan Bulat & Pecahan Kelas 7 SMP
- -2
- -1
- 0
- 1
PEMBAHASAN :
-25 – (- 24) = -25 + 24 = 24 – 25 = -1
Maka -25 – (- 24) = -1
Jawaban B
- -12
- -6
- 0
- 6
- 120
- -129
- -219
- 320
PEMBAHASAN :
525 : (-5) + 6 – 8 x 15
⇒ [525 : (-5)] + 6 – [8 x 15]
⇒ -105 + 6 – 120 = -219
Jawaban C
Urutan pecahan terkecil ke pecahan terbesar dari 0,45; 0,85;
PEMBAHASAN :
Ubah bentuk pecahan menjadi desimal, sehingga :
![]()
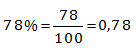
0,45; 0,85; ![]() ; dan 78% = 0,45 ; 0,85; 0,875; 0,78
; dan 78% = 0,45 ; 0,85; 0,875; 0,78
maka jika diurutkan dari yang terkecil ke yang terbesar
0,45; 0,78; 0,85; 0,875 atau
0,45; 78%; 0,85; ![]()
Jawaban B
- Rp. 60.000
- Rp. 100.000
- Rp. 120.000
- Rp. 150.000
PEMBAHASAN :
Menentukan sisa uang Andi pada hari ke-11
Sisa Uang Andi = (Uang awal) – (Uang yang di belanjakan tiap hari x jumlah hari)
= (Rp. 450.000) – (Rp. 30.000 x 11 hari)
=Rp. 450.000 – Rp. 330.000
= Rp. 120.000
Maka sisa uang Andi setelah 11 hari adalah Rp. 120.000
Jawaban C
PEMBAHASAN :
Perkalian dan pembagian dalam pecahan memiliki kedudukan yang sama kuat, sehingga pengoperasiannya dapat dimulai dari kiri ke kanan
![]()
![]()
Jawaban D
- 37,5%
- 25 %
- 15%
- 10%
PEMBAHASAN :
Jumlah murid dalam satu kelas = 25 + 15 = 40 orang
Maka persentase jumlah murid perempuan di dalam satu kelas adalah:
![]()
Jawaban A
- -1
- -3
- -2
- -4
PEMBAHASAN :
8 x (4x – 2) = 48
maka 4x – 2 = 6, karena 8 x 6 = 48
Sehingga:
4x – 2 = 6
4x = 6 + 2 = 8
x = 2
Invers dari 2 adalah -2
Jawaban C
- 6
- 8
- 10
- 12
PEMBAHASAN :
Faktorisasi prima dari 72 adalah 32 x 8
Faktorisasi prima dari 64 adalah 23 x 8
Faktorisasi prima dari 48 adalah 2 x 3 x 8
Maka FPB dari 72, 64 dan 48 adalah 8
Jawaban B
- 55
- 60
- 65
- 70
PEMBAHASAN :
Jumlah Soal = 35 soal
Soal yang dijawab = 20 soal
Soal yang tidak diisi = 15 soal
Jawaban benar = 20 – 5 = 15
Jawaban salah = 5
Maka nilai siswa tersebut adalah
nilai = (jawaban benar x 4) + (jawaban salah x 5) = (15 x 4) + (5 x (-1)) = 60 – 5 = 55
Jawaban A
- 0
- – 5
- – 10
- 3
PEMBAHASAN :
Perhatikan garis bilangan di bawah ini!

Pada garis bilangan berlaku semakin ke kanan, nilai bilangan semakin besar sedangkan semakin ke kiri, nilai bilangan semakin kecil.
Maka nilai yang paling rendah adalah – 10
Jawaban C
- – 5
- – 25
- 25
- 5
PEMBAHASAN :
-15 – 10 = -25
Jawaban B
- 300 C
- 200 C
- 320 C
- 400 C
PEMBAHASAN :
Menghitung perubahan suhu pada permukaan laut:
![]()
Maka suhu pada ketinggian 3.200 m di atas permukaan laut:
380 C – 80 C = 300 C
Jawaban A
Hasil perhitungan dari 16 x ( – 5) x 12 adalah …
- 560
- – 480
- 740
- -960
PEMBAHASAN :
16 x ( – 5) x 12 = – 80 x 12 = – 960
Jawaban D
- 4
- 5
- 6
- 7
PEMBAHASAN :
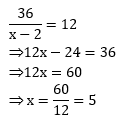
Jawaban B

I thank the teacher,who has summarized this math material, it really helps me in learning
TERIMAKASIH SUDAH SANGAT MEMBANTU
Terimakasih🙏