Contoh Soal & Pembahasan Bangun Ruang Tingkat SMP

1. 3.200 cm³
2. 3.375 cm³
3. 4.324 cm³
4. 5.432 cm³

PEMBAHASAN :
Diketahui luas permukaan = 1350 cm²
Menentukan rusuk kubus
Luas permukaan = 6s² = 1350 cm²
⇔ s² = 225 cm²
⇔ s = 15 cm²
Maka volume kubusnya adalah
volume kubus = sisi x sisi x sisi = 15 x 15 x 15 = 3.375 cm³
Jawaban B

Limas memiliki alas persegi dengan panjang diagonal . Jika tinggi limas 12 cm, maka volume limas tersebut adalah….

1. 400 cm³
2. 425 cm³
3. 450 cm³
4. 500 cm³

PEMBAHASAN :
Diketahui:
panjang diagonal =
Panjang diagonal persegi memiliki rumus =
maka panjang sisi perseginya (s) adalah 10
Maka volume limasnya adalah
V = x s x s x t = x 10 x 10 x 12 = 400 cm³
Jawaban A

1. 15 cm
2. 20 cm
3. 22 cm
4. 25 cm

PEMBAHASAN :
Diketahui:
Volume kerucut (V) = 6.541 cm³
tinggi (t) = 10 cm
Maka jari-jari kerucut tersebut adalah
V = x π x r² x t
6.541 = x 3,14 x r² x 10

Jawaban D

1. 650 cm³
2. 700 cm³
3. 735,8 cm³
4. 753,6 cm³

PEMBAHASAN :
Menentukan tinggi kerucut (t)

Maka volume bangun ruang tersebut adalah
V = volume kerucut + volum setengah bola


Jawaban D

1. 165,23 cm²
2. 170,12 cm²
3. 175,53 cm²
4. 182,32 cm²

PEMBAHASAN :
Diketahui:
Volume kerucut (V) = 250 cm³
diameter kerucut (d) = 10 cm, maka jari-jarinya (r) = 5 cm
Menentukan tinggi kerucut (t)
V = x π x r² x t
261,7 = x 3,14 x 5² x t
785 = 78,5t
t = 10 cm
Menentukan panjang garis pelukis (s)

Maka luas selimut kerucut adalah
Luas selimut = πrs = 3,14 x 5 x 11,18 = 175,53 cm²
Jawaban C

1. 8.531 cm²
2. 9.420 cm²
3. 9.630 cm²
4. 9.7450 cm²

PEMBAHASAN :
Diketahui:
Keliling (K) = 157 cm
tinggi (t) = 35 cm
Menentukan jari-jari (r) dari keliling
K = 2πr
157 = 2. 3,14. r
6,28r = 157
r = 25
Maka luas permukaan tabung tersebut adalah
Luas tabung = 2πr(r+t) = 2. 3,14. 25 (25+35) = 9.420 cm²
Jawaban B

1. Rp. 3.232.500
2. Rp. 3.421.000
3. Rp. 3.632.500
4. Rp. 3.846.500

PEMBAHASAN :
Diketahui:
Diameter drum (d) = 70 cm, maka jari-jari (r) = 35 cm
tinggi drum = 1 meter = 100 cm
Maka volume minyak kelapa dalam drum tersebut adalah
V = πr²t = 3,14 x 35² x 100 = 384.650 cm³ = 384,650 dm³ = 384,650 liter
Maka uang yang harus dikeluarkan pa Arman adalah
384,650 liter x Rp. 10.000/liter = Rp. 3.846.500
Jawaban D

PEMBAHASAN :
Diketahui:
jari-jari (r) = 15 cm
tinggi (t) = 20 cm
Menentukan luas permukaan tabung tanpa tutup
luas permukaan tabung tanpa tutup = luas alas + luas selimut
L = πr² + 2πrt
L = (3,14 x 15 x 15) + (2 x 3,14 x 15 x 20)
L = 706,5 + 1884
L = 2590,5 cm²
Jawaban A

PEMBAHASAN 
Diketahui:
panjang (p) = 10 cm
lebar (l) = 6 cm
tinggi (t) = 4 cm
maka panjang diagonal ruang balok tersebut adalah


Jawaban C

1. 25 cm
2. 30 cm
3. 35 cm
4. 40 cm

PEMBAHASAN :
Diketahui:
Volume air dalam tangki (V) = 100 liter = 100.000 cm³
tinggi tangki (t) = 80 cm
Menentukan diameter tangki dari volume
V = πr²t
100.000 = 3,14.r² . 79,62 cm
250r² = 100.000
r² = 400
r = 20 cm
maka diameternya adalah 2r = 2.20 = 40 cm
Jawaban D

1. 21.500 cm³
2. 23.775 cm³
3. 25.645 cm³
4. 26.895 cm³

PEMBAHASAN :
Diketahui:
p = 30 cm
t = 25 cm
panjang semua rusuk = 260 cm

menghitung lebar kotak, sebagai berikut:
3(p + l + t) = 260 cm
3(30 cm + l + 25 cm) = 260 cm
165 cm + 3l = 260 cm
3l = 95 cm
l = 31,7 cm

maka volume kotak dapat dihitung sebagai berikut:
v = p x l x t
v = 30 cm x 31,7 cm x 25 cm = 23.775 cm³
Jawaban B

1. 3.552 cm²
2. 3.225 cm²
3. 4.456 cm²
4. 4.327 cm²

PEMBAHASAN :
Diketahui:
p : l : t = 10 : 7 : 3
Panjang semua rusuk = 240 cm

Menentukan panjang, lebar, dan tinggi balok, sebagai berikut:
3(p + l + t) = 240 cm
p + l + t = 80 cm

Maka:

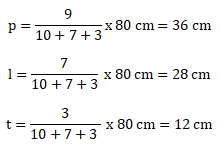
Sehingga luas permukaan balok dapat dihitung sebagai berikut:
Luas permukaan balok = 2(pl + pt + lt) = 2 {(36 x 28) + (36 x 12) + (28 x 12)}
.                                          = 2 (1008 + 432 + 336)
.                                          = 3.552 cm²
Jawaban A

1. 245
2. 298
3. 324
4. 357

PEMBAHASAN :
Diketahui:
Panjang sisi miring = 15 cm
Panjang alas = 9 cm
Tinggi prisma = 18 cm

Menentukan tinggi segitiga siku-siku, sebagai berikut:

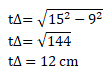
Maka volume prisma dapat dihitung sebagai berikut:

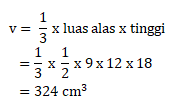
Jawaban C

1. 4.987
2. 5.184
3. 5.356
4. 6.122

PEMBAHASAN :
Diketahui:
Panjang diagonal = 36 cm
Panjang diagonal ruang = , maka:

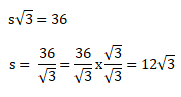
Maka volume kubus dapat dihitung sebagai berikut:
v = s³ = ()³ = 5.184 cm³
Jawaban B

1. 2.456 cm³
2. 2.987 cm³
3. 3.235 cm³
4. 3.672 cm³

PEMBAHASAN :
Perhatikan gambar alas prisma di bawah ini!

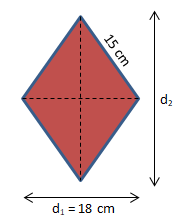
Diketahui:
Panjang sisi alas = 15 cm
d₁ = 18 cm
t prisma = 17 cm

Menentukan diagonal yang ke-2 (d₂ ) sebagai berikut:

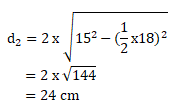
Maka, volume prisma dapat dihitung sebagai berikut:

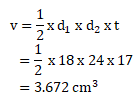
Jawaban D

1. 3.165 cm³
2. 3.564 cm³
3. 3.654 cm³
4. 3.666 cm³

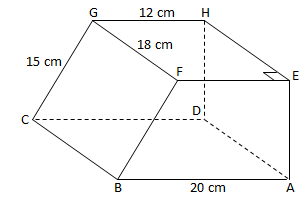
PEMBAHASAN :
Diketahui:
CG = 15 cm
FG = 18 cm
GH = 12 cm
AB = 20 cm

Menentukan tinggi prisma (AE), yaitu:
                `                                                                   `
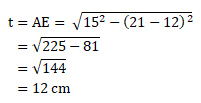Maka volume trapesium dapat dihitung sebagai berikut:
V = luas trapesium x tinggi trapesium
V =[ ½ x (12 + 21) x 12] x 18 = (198) x 18 = 3.564 cm³
Jawaban B

1. 1.890 cm³
2. 2.304 cm³
3. 3.678 cm³
4. 4.112 cm³

PEMBAHASAN :
Diketahui:
Luas alas = 192 cm²
Tinggi limas = 36 cm

Menentukan volume limas
v = 1/3 x luas alas x tinggi = 1/3 x 192 cm² x 36 cm = 2.304 cm³
Jawaban B

1. 1.134 cm³
2. 2.334 cm³
3. 3.250 cm³
4. 4.145 cm³

PEMBAHASAN :
Diketahui:
S = 30 cm
d = 24 cm, maka r = 12 cm
π = 3,14

Menentukan tinggi kerucut, sebagai berikut:

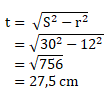
Maka volume kerucut tersebut dapat dihitung sebagai berikut:
v = 1/3 x π x r² x t
v = 1/3 x 3,14 x 12² x 27,5 = 4.145 cm³
Jawaban D

1. 1.248 cm²
2. 1.456 cm²
3. 1.578 cm²
4. 1.980 cm²

PEMBAHASAN :
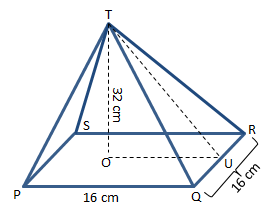
Diketahui:
PQ = QR = 16 cm
OT = 32 cm

Menentukan tinggi limas, sebagai berikut:

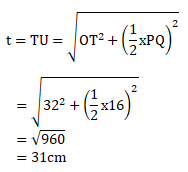
Maka luas permukaan limas dapat dihitung sebagai berikut:
L = L alas + (4 x L segitiga)
L = (16 x 16) + 4 x ( ½ x 16 x 31) = 256 + 992 = 1.248 cm²
Jawaban A

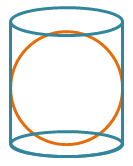
1. 3 : 2
2. 3 : 4
3. 1 : 2
4. 2 : 3

PEMBAHASAN :
Diketahui:
r tabung = r bola
tinggi tabung = diameter bola = 2r
V_tabung = πr² t
V_bola = 4/3 πr³

Maka perbandingan volume tabung dan bola dapat dihitung sebagai berikut:

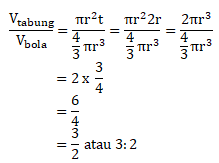
Jawaban A