Soal No.21 (SBMPTN 2014)
Diketahui a, a+b, a+5b merupakan 3 suku pertama suatu barisan geometri. Jika a, a+b, x, y dan z merupakan 5 suku pertama barisan aritmetika dan x + y + x = -15, maka suku ke 10 barisan aritmetika tersebut adalah…
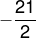
- -14
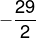
- -15
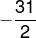
PEMBAHASAN :

Jawaban : B
Soal No.22 (UN 2014)
Jumlah konsumsi gula pasir oleh penduduk suatu kelurahan pada tahun 2013 sebesar 1.000 kg dan selalu meningkat dua kali lipat setiap tahun. Total konsumsi gula penduduk tersebut tersebut pada tahun 2013 sampai dengan tahun 2018 adalah …
- 62.000 kg
- 63.000 kg
- 64.000 kg
- 65.000 kg
- 66.000 kg
PEMBAHASAN :

Jawaban : B
Soal No.23 (SBMPTN 2014)
Jika S = 1 +

sin2x +

sin
22x +

sin
3 2x+…
 < S < 2
< S < 2 < S < 2
< S < 2 < S <
< S < 
 < S <
< S < 
 < S <
< S < 
PEMBAHASAN :

Jawaban : A
Soal No.24 (UN 2014)
Seutas tali dipotong menjadi 5 bagian sehingga panjang potongan-potongan tali tersebut membentuk barisan geometri. Jika panjang potongan tali terpendek 6 cm dan tali terpanjang 96 cm maka panjang tali semula adalah ..
- 96 cm
- 185 cm
- 186 cm
- 191 cm
- 192 cm
PEMBAHASAN :
Diketahui:
n = 5
a = 6
Menentukan rasio (r)
U5 = ar4
96 = 6r4
r4 = 16
r = 2
Menentukan panjang tali semula

Jawaban : C
Soal No.25 (UN 2010)
Tiga buah bilangan membentuk barisan aritmatika dengan beda tiga. Jika suku kedua dikurangi 1,maka terbentuklah barisan geometri dengan jumlah 14. Rasio barisan tersebut adalah …
- 4
- 2

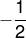
- -2
PEMBAHASAN :
Misal tiga buah bilangan tersebut adalah:
x – 3, x, x + 3
Diketahui jumlah barisan geometri = 14, jika suku kedua dikurangi 1, Maka:
(x – 3) + (x – 1) + (x + 3) = 14
x = 5
deret aritmatika : 2, 4, 8

Jawaban : B
Soal No.26 (UN 2007)
Bakteri jenis A berkembang biak menjadi dua kali lipat setiap lima menit. Pada waktu lima belas menit pertama banyaknya bakteri ada 400. Banyak bakteri pada waktu tiga puluh menit pertama adalah …
- 640 bakteri
- 3.200 bakteri
- 6.400 bakteri
- 12.800 bakteri
- 32.000 bakteri
PEMBAHASAN :
Diketahui U3 = 400 (lima belas menit pertama)
Menentukan jumlah bakteri awal (a)
U3 = 400
ar3 = 400
a.23 = 400
a = 50
Menentukan jumlah bakteri tiga puluh menit pertama (U7)
U7 = ar7= 50(2)6 = 64.000 bakteri
Jawaban : C
Soal No.27 (UN 2009)
Sebuah ayunan mencapai lintasan pertama sejauh 90 cm dan lintasan berikutnya hanya mencapai

dari lintasan sebelumnya. Panjang lintasan seluruhnya hingga ayunan berhenti adalah….
- 120 cm
- 144 cm
- 240 cm
- 250 cm
- 260 cm
PEMBAHASAN :

Jawaban : C
Soal No.28 (UN 2013)
Sebuah bola tenis di jatuhkan dari ketinggian 2 m dan memantul menjadi

tinggi sebelumnya. Panjang lintasan bola tenis tersebut sampai berhenti adalah…
- 8 m
- 16 m
- 18 m
- 24 m
- 32 m
PEMBAHASAN :

Jawaban : C
Soal No.29
Suku ke-3 dan 8 suatu barisan aritmetika berturut-turut adalah 120 dan 150. Suku ke-25 barisan tersebut adalah …
- 252
- 515
- 525
- 350
- 253
PEMBAHASAN :
Diketahui:
U3 = 120
U8 = 150
Berlaku: Un = a + ( n – 1) b
Jika Uk = p dan Um = q
Maka:




U3 = 120, n = 3
a + (n-1)b = 120
a + 2.6 = 120
a + 12 = 120
a = 108
Jadi suku ke-25 (n = 25) dapat dihitung sebagai berikut:
U25 = 108 + (25 – 1) 6
= 108 + 144
= 252
Jawaban : A
Soal No.30
Suku ke-3 dan 8 suatu barisan aritmetika berturut-turut adalah 120 dan 150. Suku ke-25 barisan tersebut adalah …
- 5520
- 5150
- 5250
- 5500
- 5110
PEMBAHASAN :





= 5050 + 100
= 5150
Jawaban : B
< S < 2
< S < 2
< S <
< S <
< S <

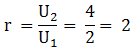
![]()
![]()
![]()
![]()




![]()




