Contoh Soal Fungsi & Komposisi Jawaban dan Pembahasannya Kelas 10
- -27
- -9
- 0
- 3
- 9
PEMBAHASAN :
h(x) = (fog)(x) = f(g(x))
h'(x) = g'(x).f'(g(x))
h'(2) = g'(2).f'(g(2))
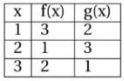
Dengan melihat tabel fungsi f(x), g(x) serta kurva f'(x), g'(x), didapat:
g(2) = 3, g'(2) = 3, f'(3) = -3
Maka:
h'(2) = 3. f'(3) = 3. (-3) = -9
Jawaban B
- x2 + 3x + 3
- x2 + 3x + 2
- x2 – 3x + 3
- x2 + 3x – 1
- x2 + 3x + 1
PEMBAHASAN :
Menentukan (f ◦ g)(x)
(f ◦ g)(x)= f (g (x)) = f (x + 1) = (x + 1)2 + (x + 1)- 1
(f ◦ g)(x)= x2 + 2x + 1 + x = x2 + 3x + 1
Jawaban : E
- -3
- -2


- 3
- -6
- -3
- 3
- 3 atau -3
- 6 atau -6
PEMBAHASAN :
Menentukan nilai x
(f ◦ g)(x) = -4
f(g (x)) = -4
f(2x – 6) = -4
(2x – 6)2 – 4 = -4
2x – 6 = 0
x = 3
Jawaban : C
- -4
- -2
- -1
- 1
- 4
PEMBAHASAN :
f (x) = y ↔ f -1 (y) = x
f (5) = y
f –1 (4x-5) = 3x-1
sehingga 3x-1 = 5
x = 2 dan y = 4x-5 = 3
x = 2
Menentukan nilai p
(f– -1 ◦ f)(5) = p2 + 2p-10
f -1 (f(5)) = p2 + 2p – 10
f—1(3) = p2 + 2p – 10
3(2)-1 = p2 + 2p – 10
p2 + 2p – 1 = 0
(p + 5)(p – 3) = 0
p = -5 dan p = 3
Jadi, rata-rata nilai p adalah ![]() = -1
= -1
Jawaban : C
- 30
- 60
- 90
- 120
- 150
PEMBAHASAN :
Menentukan nilai p
g (f (x)) = f (g (x))
g (2x + p) = f (3x + 120)
3 (2x + p) + 120 = 2 (3x + 120) + p
6x + 3p + 120 = 6x + 240 + p
2p = 120
p = 60
Jawaban : B
- -∞ < x < ∞
- 1 ≤ x ≤ 2
- x ≥ 0
- x ≥ 1
- x ≥ 2
- x2 – 3x + 3
- x2 – 3x + 11
- x2 – 11x + 15
- x2 – 11x + 27
- x2 – 11x + 35
PEMBAHASAN :
Menentukan (g ◦ f)(x)
(g ◦ f)(x)= g (f (x)) = g (x – 4) = (x – 4)2 – 3(x – 4) + 7 = x2 – 8x + 16 – 3x + 12 + 7
(g ◦ f)(x) = x2 – 11x + 35
Jawaban : E
- 0
- 1
- 3
- 4
- 5
PEMBAHASAN :
Menentukan g(x)
(g ◦ f)(x) = 2x2 + 4x – 6
g(f(x)) = 2x2 + 4x – 6
g(x+2) = 2x2 + 4x -6
g(x) = 2(x – 2)2 + 4(x – 2) – 6 = 2x2 – 8x + 8 + 4x – 8 – 6 = 2x2 – 4x – 6
menentukan x1 + 2x2
g(x) = 0
2x2 – 4x – 6 = 0
x2 – 2x – 3 = 0
(x-3)(x+1) = 0
x1=3 →x2 = -1, jadi 3
x1 = 2x2 = 3+2 (-1) = 1
atau
x1 = -1 → x2 = 3, jadi
x1 + 2x2 = (-1) + 2(3) = 5
Jawaban : E
- x2 + 2x + 1
- x2 + 2x + 2
- 2x2 + x + 2
- 2x2 + 4x + 2
- 2x2 + 4x + 1
PEMBAHASAN :
Menentukan f(x)
(g ◦ f)(x) = 2x2 + 4x + 5
g(f(x)) = 2x2 + 4x + 5
2(f(x)) + 3 = 2x2 + 4x + 5
f(x) = x2 + 2x + 1
Jawaban : A

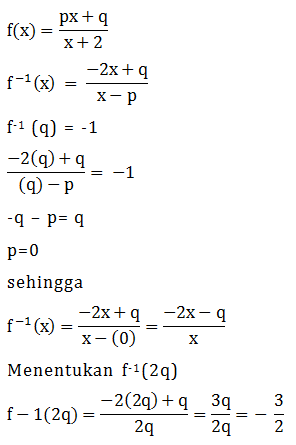
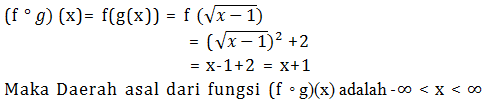
Terimakasih banyak. Jadi terbantu sekali. Contoh soal juga lengkap