DAFTAR ISI
Rangkuman Materi Teori Kinetik Gas Kelas 11
GAS IDEAL
Sifat-Sifat Gas Ideal
- Berlaku hukum Newton tentang gerak
- Partikel gas selalu bergerak secara acak atau sembarangan.
- Tidak ada gaya tarik menarik/interaksi antarmolekul.
- Ukuran molekul gas dapat diabaikan terhadap ukuran ukuran ruangan tempat gas berada.
- partikel gas terdistribusi merata dalam ruangan.
- Tumbukan antar partikel bersifat lenting sempurna.
Hukum-hukum tentang Gas
Hukum Boyle
“pada suhu yang dibuat tetap, perkalian tekanan dan volume selalu konstan/tetap”.
Sehingga berlaku persamaan berikut :
PV = konstan
P1V1 = P2V2
Hukum Charles
“pada tekanan yang dibuat tetap, hasil bagi volume terhadap suhu akan selalu bernilai konstan/tetap”.
atau :
“pada volume yang dibuat tetap, hasil bagi tekanan terhadap suhu akan selalu bernilai konstan/tetap “.
atau:
Hukum boyle-gay lussac
merupakan gabungan dari hukum boyle ,hokum charles , dan hokum gay lussac .di dapat persamaan berikut:
Keterangan :
P1= Tekanan awal (N/m2)
P2=Tekanan akhir (N/m2)
V1=Volume awal(m3)
V2=Volume akhir (m3)
T1=Suhu awal (K)
T2=suhu akhir (K)
Persamaan umum gas ideal
Dirumuskan sebagai berikut:
PV = NkT atau PV = nRT
Keterangan:
P = tekanan gas ideal (N/m2)
V = volume gas ideal(m3)
N = jumlah molekul zat
n = jumlah mol
k = konstanta Boltzmann(dimana k = 1,38 x 10-23J/K)
R = konsanta gas umum (dimana R=8,31J/Mol K)
T = suhu gas ideal (K)
mol zat (n) dapat ditentukan dengan persamaan.
Keterangan:
N = jumlah molekul zat
NA=bilangan Avogadro (6,02 x 1023 partikel)
m= massa partikel gas (gram)
Mr=massa relatif molekul gas
Hubungan Kecepatan Partikel Gas, Energi Kinetik Dan Tekanan
Dalam gas ideal tekanan , suhu, dan kecepatan dapat ditentukan dengan persamaan berikut.
Energi kinetik
Tekanan gas
Suhu gas
Keterangan:
N = jumlah partikel zat
EK = energi kinetik rata-rata(J)
M0 = massa partikel gas (kg)
Mr = massa molekul relatif (kg/mol)
ρ = massa jenis gas ideal(kg/m3)
k = konstanta Boltzmann(dimana k = 1,38 x 10-23J/K)
R = konsanta gas umum (dimana R=8,31J/Mol K)
T = suhu (kelvin)
Energi Dalam
yaitu energi kinetik partikel gas yang terdapat di dalam suatu ruang tertutup
U = N.Ek = Nf(½ KT)
Keterangan:
N =jumlah partikel
Ek = energi kinetik
f = derajat kebebasan
- Gas monoatomic(f=3 seperti He , Ne, dan Ar)
- Gas diatomi seperti H2,O2,N2
Suhu rendah (T = ±250k ), f=3
Suhu rendah (T = ±500k), f=5
Suhu tinggi (T= ± 1000 k ), f=7
Contoh Soal Teori Kinetik Gas Pembahasan & Jawaban Kelas 11
PEMBAHASAN :
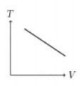
Perhatikan grafik berikut.
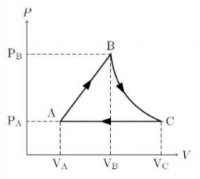
Jika gas argon dianggap sebagai gas ideal, maka berlaku PV = nRT dari persamaan ini diperoleh hubungan V dan T sebagai berikut.
![]()
Jika perubahan diaggap kuasistatik (n = tetap) maka persamaan tersebut menjadi ![]() (k = Konstanta, anggap nilainya 1), jika dimisalkan VA = 1 m3; VB = 2 m3 ; PA = 1 Pa; PB = 2 Pa maka diperoleh TA = 1 dan TB = 4 Berdasarkan pemisalan inilah grafik T terhadap V untuk proses AB adalah grafik linear ke atas.
(k = Konstanta, anggap nilainya 1), jika dimisalkan VA = 1 m3; VB = 2 m3 ; PA = 1 Pa; PB = 2 Pa maka diperoleh TA = 1 dan TB = 4 Berdasarkan pemisalan inilah grafik T terhadap V untuk proses AB adalah grafik linear ke atas.
Jawaban A
- Temperatur gas bertambah meskipun energi dalamnya tetap
- Temperatur gas bertambah tanpa gas melakukan usaha
- Energi dalam gas berkurang karena sebagian berubah mejadi kalor
- Gas melakukan usaha sebesar penambahan energi dalamnya
- Temperatur gas bertambah sebanding dengan penambahan kelajuan molekul gas
PEMBAHASAN :
Dari rumusan kecepatan efektif gas ideal kita dapat melihat hubungan temperatur dan kelajuan molekul gas
![]()
Dari rumusan tersebut terlihat bahwa temperatur (T) dengan kelajuan molekul gas (vrms) sebanding. Maka jika temperatur dinaikan maka terjadi penambahan kelajuan molekul gas
Jawaban : E
Gas Argon dianggap sebagai gas ideal. Gas itu mula- mula mempunyai energi dalam Ei dan temperatur Ti. Gas tersebut mengalami proses dengan melakukan usaha W, melepaskan energi senilai Q, dan keadaan akhir energi dalam Ef serta temperatur Tf. Besarnya perubahan energi tersebut digambarkan seperti gambar berikut.
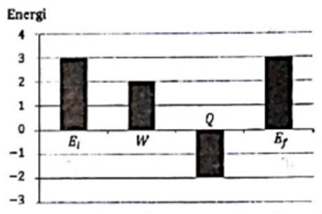
Apa simpulan proses tersebut.
- Gas mengalami proses isobarik dan Tf < Ti
- Gas mengalami proses adiabatik dan Tf < Ti
- Gas mengalami proses isokhorik dan Tf < Ti
- Gas mengalami proses isotermal dan Tf = Ti
- Gas mengalami proses isokhorik dan Tf = Ti
PEMBAHASAN :
Diketahui dari grafik
Ei = Ui = 3 J
Ef = Uf = 3 J
Menentukan energi dalam (ΔU)
ΔU = UF – Ui
ΔU = 3 – 3
ΔU = 0
ΔU = 3/2 n. R. ΔT
0 = 3/2 n. R. ΔT
Maka ΔT = 0, karena n ≠ 0
Karena ΔT = 0, maka tidak terjadi perubahan suhu atau disebut isotermis
Tf = Ti
Jawaban : D
- 1:3
- 1:2
- 2:3
- 3:4
- 4:3
PEMBAHASAN :
- 600 oC
- 450 oC
- 327 oC
- 300 oC
- 54 oC
- 4
- 2
- 1/√2
- √2
- 1/2
PEMBAHASAN :
Jawaban : C
- Makin tinggi suhu gas, energi kinetiknya makin kecil
- Makin tinggi suhu gas, gerak partikel gas makin lambat
- Makin tinggi suhu gas, gerak partikel makin cepat
- Suhu gas berbanding terbalik dengan energi kinetik gas
- Suhu gas tidak mempengaruhi gerak partikel gas
PEMBAHASAN :
Dari rumus Ek = 3/2 kT, suhu berbanding lurus dengan energi kinetik. Jika suhu dinaikkan maka energi kinetiknya makin besar. Semakin besar energi kinetik gerak partikel gas akan bergerak semakin cepat
Jawaban : C
suhu gas nitrogen pada saat kelajuan rms-nya (root mean square) sama dengan v1 adalah 300 K jika kelajuan rms gas nitrogen diperbersar menjadi dua kali dari v1 maka suhu gas nitrogen tersebut berubah menjadi ……….
- 425 K
- 600 K
- 1.146 K
- 1.200 K
- 2. 292 K
PEMBAHASAN :
Jawaban : D
- ¼ kali semula
- ½ kali semula
- Sama dengan semula
- 2 kali semula
- 4 kali semula
- 1 : 4
- 1 : 2
- 2 : 1
- 4 : 1
- 5 : 1
- 2.983,1 liter
- 1.964,2 liter
- 298,3 liter
- 196,4 liter
- 94,2 liter
- 75,25 x 105 N/m2
- 75,25 x 103 N/m2
- 75,25 x 102 N/m2
- 75,25 x 10-3 N/m2
- 75,25 x 10-5 N/m2
PEMBAHASAN :
Diketahui:
V = 2 m3
n = 15 mol
Ek = 2,5 x 10-20 J
NA = 6,02 x 1023 molekul/mol
Menghitung jumlah molekul dalam bejana sebagai berikut:
N = n x NA
= 15 mol x 6,02 x 1023 molekul/mol
= 90,3 x 1023 molekul
Maka tekanan gas dalam bejana dapat dihitung sebagai berikut:

Jawaban : B
- 0,01 kg
- 0,04 kg
- 0,1 kg
- 0,6 kg
- 0,08 kg
PEMBAHASAN :
Diketahui:
V = 2.500 cm3 = 2,5 x 10-3 m3
T = 220C = (22 + 273)K = 2950K
pr = 20 atm
M = 34 kg/kmol
P0 = 2 atm
R = 8,314 J/molK
Menghitung total tekanan pada sistem sebagai berikut:
p = p0 + pr
= 2 atm + 20 atm
= 22 atm
= 22 x 105 Pa
Maka massa oksigen dapat dihitung sebagai berikut:
pV = nRT

Jawaban : E
- 12367,051 J
- 21213,012 J
- 11149,074 J
- 14562,022 J
- 21167,033 J
PEMBAHASAN :
Diketahui:
V = 0,5 m3
n = 3 mol
T = 250C = (25 + 273) = 2980K
Maka energi kinetik Helium dapat dihitung sebagai berikut:

Jawaban : C
- 533 m/s
- 431 m/s
- 389 m/s
- 465 m/s
- 587 m/s
PEMBAHASAN :
Diketahui:
M = 40 kg/kmol
T = 250C = kg/kmol = (25 + 273)K = 2980K
NA = 6,02 x 1026 partikel/kmol
k = 1,38 x 10-23 J/K
Menghitung massa satu partikel oksigen sebagai berikut:

Maka laju efektif gas oksigen dapat dihitung sebagai berikut:

Jawaban : B
- 9353,25 J
- 2899,56 J
- 8432,21 J
- 4999,30 J
- 8946,87 J
PEMBAHASAN :
m = 10 g
Mr = 4 g/mol
T = 270C = (27 + 273)K = 300 K
R = 8,314 J/molK
Suhu gas Helium 300 k, bersuhu rendah. Maka berlaku:

Jawaban : A
- 1ρ
- 2ρ
- 3ρ
- 4ρ
- 5ρ
PEMBAHASAN :
Diketahui:
T1 = T
p1 = p
ρ1 = ρ
T2 = 0,5 T
p2 = 2p
Berlaku persamaan gas ideal sebagai berikut:

Maka rapat massa gas akhir dapat dihitung sebagai berikut:

ρ2 = 4ρ1
ρ2 = 4ρ
Jawaban : D
- 10.125 gr
- 8.130 gr
- 9.753 gr
- 8.150 gr
- 11.100 gr
PEMBAHASAN :
Diketahui:
V1 = 20.000 liter
p1 = 15 atm
T1 = 270 C = (27 + 273) K = 300 K
p2 = 10 atm
R = 0,082 liter.atm/mol.K
Mr = 2 gr/mol
Untuk menghitung banyaknya mol gas hydrogen dalam tangki mula-mula dan akhir berlaku rumus sebagai berikut:

Banyak mol gas hidrogen yang keluar sebagai berikut:
n = n1 – n2
= 12,195 x 103 mol – 8,130 x 103 mol
= 4,065 x 103 mol
= 4.065 mol
Maka massa gas hidrogen yang keluar dapat dihitung sebagai berikut:
m = n x Mr
= 4.065 mol x 2 gr/mol
= 8.130 gram
Jawaban : B
- 900 liter
- 1.200 liter
- 750 liter
- 1.000 liter
- 800 liter
PEMBAHASAN :
Diketahui:
V1 = 30 liter = 3 x 10-2 m3
P1 = 1,5 x 106 Pa
P2 = 1,2 x 106 Pa
P0 = 104 Pa
Menghitung volume gas dalam silinder pada suhu tetap yaitu:

Sedangkan volume gas yang keluar dari kran pada tekanan P2 yaitu:
ΔV = 37,5 liter – 30 liter = 7,5 liter
Maka volume gas yang keluar pada tekanan atmosfer dapat dihitung sebagai berikut:

Jawaban : A
- 256,8 m/s
- 561,2 m/s
- 8 m/s
- 467,5 m/s
- 458,3 m/s
PEMBAHASAN :
Diketahui:
p = 2,8 x 105 N/m2
ρ = 4 kg/m3
Maka kecepatan efektif gas dapat dihitung sebagai berikut:

Jawaban : E
- 9,76 x 10-10 Pa
- 9,76 x 10-15 Pa
- 9,76 x 10-20 Pa
- 9,76 x 10-19 Pa
- 9,76 x 10-2 Pa
PEMBAHASAN :
N = 2 atom
V = 4 cm3 = 4 x 10-6 m3
T = 5 K
Ar hidrogen = 1 gr/mol = 1 kg/kmol
R = 8,31 x 103 J/kmol K
NA = 6,02 x 1023 partikel/mol = 6,02 x 1026 partikel/kmol
Menghitung laju efektif atom sebagai berikut:

Maka tekanan udara pada tempat tersebut dapat dihitung sebagai berikut:

Jawaban : C
- 25 x 104 N/m2
- 27 x 104 N/m2
- 29 x 106 N/m2
- 33 x 103 N/m2
- 55 x 107 N/m2
PEMBAHASAN :
n = 1 mol
V = 10 m3
R = 8,31 x 103 J/mol.K
T = 270 C → 27 + 273 = 300 K
Maka besar tekanan gas dapat dihitung sebagai berikut:
PV = nRT

Jawaban : A
- 100 m/s
- 180 m/s
- 240 m/s
- 320 m/s
- 420 m/s
PEMBAHASAN :
Diketahui:
T1 = T
T2 = 16T
v1 = 60 m/s
Maka untuk menentukan kecepatan dapat dihitung sebagai berikut:

Jawaban : C
- 12,8 x 104 N/m2
- 10,5 x 106 N/m2
- 18,8 x 105 N/m2
- 20,6 x 103 N/m2
- 10,8 x 105 N/m2
PEMBAHASAN :
Diketahui:
s = 20
cm = 0,2 m
V = s3 = (0,2)3 = 8 x 10-3 m3
N = 1020
m = 8 μg = 8 x 10-19 kg
v = 18 m/s
Maka tekanan gas dapat dihitung sebagai berikut:

Jawaban : E
- 3P
- 6P
- 9P
- ½ P
- ½ P2
PEMBAHASAN :
Diketahui:
v1 = v
v2 = 3v
P1 = P
![]()
dengan P ~ v2
P1 : P2 = v12 : v22
P : P2 = v2 : (3v)2
P : P2 = 1 : 9
P2 = 9P
Jawaban : C
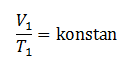
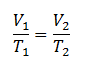

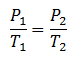

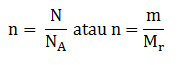
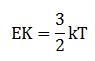
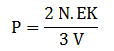
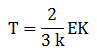
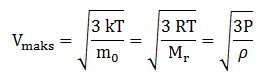

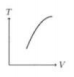
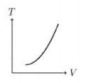
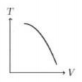




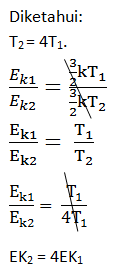


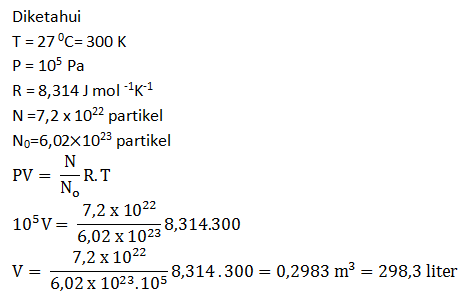
sarangheo 🙂 alhamdulillah terimakasih banyak. jazakumulah khairon katsir
mbak kalo ngucap salam harusnya kan pake assalam bukan sarangheo…orang islam lagi…
Mantap bang😂
Makasih sangat ilmunya gan.. Btw, itu yang nomer 1 perbandingannya bukan 4:3 kah? 😄