Rangkuman Materi Bangun Ruang Tingkat SD

Jaring-Jaring, Sifat-Sifat, Luas Permukaan, dan Volume Bangun Ruang

Bangun ruang terdiri atas tiga unsur sebagai berikut:

1. Sisi, adalah suatu bidang yang membatasi bagian dalam dan bagian luar bangun ruang. Sisi dapat berbentuk bidang datar ataupun bidang lengkung.
2. Rusuk, adalah pertemuan dua buah sisi yang berupa ruas garis pada bangun ruang.
3. Titik sudut, adalah titik pertemuan atau perpotongan tiga buah rusuk atau lebih pada bangun ruang.

Perhatikan contoh bangun ruang di bawah ini!

Keterangan:

• Sisi balok terdiri dari 6 sisi yaitu: PQRS, PQUT, QRUV, SRVW, PSTW, TUVW.
• Rusuk balok terdiri dari 12 rusuk yaitu: PQ, QR, RS, PS, PT, UQ, RV, WS, TU, UV, VW, TW.
• Titik sudut terdiri dari 8 titik sudut yaitu: P, Q, R, S, T, U, V, W.

Jenis-jenis bangun ruang sebagai berikut:

Balok

Gambar balok dan jaring-jaring balok

Sifat-sifat balok, sebagai berikut:

• Terdiri dari 6 sisi, 12 rusuk, dan 8 titik sudut.
• Memiliki 12 diagonal sisi atau diagonal bidang
• Memiliki 4 diagonal ruang
• Memiliki 6 bidang diagonal
• Memiliki 3 pasang bidang sama besar, berhadapan, dan sejajar
• Segiempatnya berupa persegi dan persegi panjang

Rumus yang berlaku pada bangun ruang balok:

Luas permukaan:
L = 2 {(p x l) + (p x t) + (l x t)}

Volume:
V = p x l x t

Keterangan:
p = panjang
l = lebar
t = tinggi

Bola

Gambar bola dan jaring-jaringnya

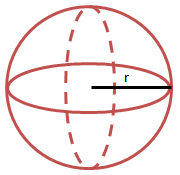
Sifat-sifat bola, sebagai berikut:

• Hanya memiliki satu buah sisi lengkung yang tertutup
• Tidak memiliki titik sudut

Rumus yang berlaku pada bangun ruang bola:

Luas permukaan:
L = 4πr²

Volume:
V = 4/3 πr³

Keterangan:
r = jari-jari
π =  = 3,14

Kerucut

Gambar dan jaring-jaring kerucut

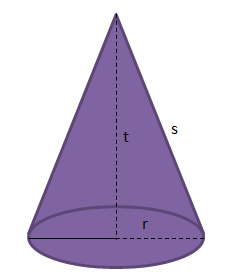
Sifat-sifat kerucut, sebagai berikut:

• Memiliki 2 sisi yang terdiri atas: sisi alas berbentuk lingkaran dan selimut (bidang lengkung) yang mengerucut ke titik puncak
• Selimut merupakan sisi tegak kerucut
• Memiliki 1 rusuk
• Tidak memiliki titik sudut, hanya memiliki titik puncak
• Tinggi kerucut yaitu jarak antara alas kerucut dan titik puncak

Rumus yang berlaku pada bangun ruang kerucut:

Luas permukaan:
L = πr(r + s)

Volume:
V = 1/3 x πr²t

Keterangan:
r = jari-jari
s = sisi apotema
π =  = 3,14

Kubus

Gambar kubus dan jaring-jaring kubus

Sifat-sifat kubus sebagai berikut:
Memiliki:

• 12 rusuk yang sama panjang
• 6 sisi yang berbentuk persegi
• 8 titik sudut
• 12 diagonal sisi/bidang
• 4 diagonal ruang
• 3 pasang bidang yang sama, sejajar, dan sebangun

Rumus yang berlaku pada bangun ruang  kubus:

Luas permukaan:
L = 6 s²

Volume:
V = s³

Keterangan:
s = sisi

Limas

Sifat-sifat limas:

• Memiliki alas berbentuk segi-n
• Penamaan sesuai dengan alasnya. Limas segi-n adalah limas yang alasnya berbentuk segi-n
• Sisi tegaknya berbentuk segitiga yang bertemu pada satu titik di puncak

Jenis-jenis limas:

Limas segitiga

Gambar dan jaring-jaring limas segitiga

Sifat-sifat limas segitiga:

• Memiliki 6 rusuk
• Memiliki 4 sisi berbentuk segitiga, 1 sisi alas dan 3 sisi tegak
• Memiliki 4 titik sudut, 1 titik sudut puncak dan 3 titik sudut pada alasnya

Limas segiempat

Gambar dan jaring-jaring limas segiempat

Sifat-sifat limas segiempat:

• Memiliki 8 rusuk
• Memiliki 5 sisi yaitu 4 sisi berbentuk segitiga dan satu sisi berbentuk persegi panjang pada alasnya
• Memiliki 5 titik sudut, 1 titik sudut puncak dan 4 titik sudut pada alasnya
• Memiliki 2 diagonal sisi/ bidang
• Tidak memiliki diagonal ruang

Limas segilima

Gambar dan jaring-jaring limas segilima

Sifat-sifat limas segilima sebagai berikut:

• Memiliki 6 sisi, 1 sisi alas dan 5 sisi tegak
• Memiliki 6 titik sudut, 1 titik sudut puncak dan 5 titik sudut pada alasnya
• Memiliki 10 rusuk

Limas segienam

Gambar dan jaring-jaring limas segienam

Sifat-sifat limas segienam sebagai berikut:

• Memiliki 7 sisi, 1 sisi alas dan 6 sisi tegak
• Memiliki 12 rusuk
• Memiliki 7 titik sudut, 1 titik sudut puncak dan 6 titik sudut pada alasnya

Rumus yang berlaku pada bangun ruang limas:

Luas permukaan:
L = L_a + jumlah luas sisi-sisi tegak

Volume:
V = 1/3 x (L_a x t)

Keterangan:
L_a = luas alas
t = tinggi

Prisma

Sifat-sifat prisma:

• Dibatasi oleh bidang-bidang tegak
• Bidang alas dan atap sejajar, memiliki ukuran dan bentuk yang sama
• Penamaan sesuai dengan alasnya. Prisma segi-n adalah prisma dengan alas dan atap berbentuk segi-n

Jenis-jenis prisma:

Prisma segitiga

Gambar dan jaring-jaring prisma segitiga

Sifat-sifat prisma segitiga sebagai berikut:

• Memiliki 6 titik sudut
• Memiliki 9 rusuk
• Memiliki 3 buah rusuk tegak berbentuk persegi panjang
• Bidang alas dan atap berbentuk segitiga
• Memiliki 5 sisi

Prisma segiempat

Prisma segiempat adalah kubus dan balok.

Prisma segilima

Gambar dan jaring-jaring segilima

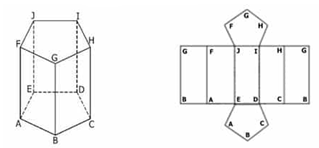
Sifat-sifat segilima sebagai berikut:

• Memiliki 10 titik sudut
• Memiliki 7 sisi yaitu 5 sisi samping, 2 sisi pada alas dan atap
• Memiliki 15 rusuk
• Memiliki 5 rusuk tegak
• Prisma segienam

Gambar dan jaring-jaring segienam

Sifat-sifat prisma segienam sebagai berikut:

• Memiliki 12 titik sudut
• Memiliki 8 sisi yaitu 6 sisi samping, 2 sisi alas dan atap
• Memiliki 18 rusuk dengan 6 rusuk tegak

Rumus yang berlaku pada bangun ruang prisma:

Luas permukaan:
L = (2 x L_a ) + (K + t)

Volume:
V = L_a  x t

Keterangan:
L_a = luas alas
K = keliling alas
t = tinggi

Tabung

Gambar dan jaring-jaring tabung

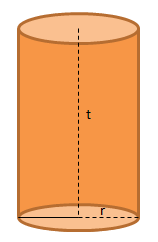
Sifat-sifat tabung sebagai berikut:

• Memiliki 3 sisi yaitu sisi alas, sisi atap, dan sisi selimut
• Bidang alas dan atap berbentuk lingkaran
• Tidak memiliki titik sudut
• Tinggi tabung adalah jarak antara lingkaran alas dan lingkaran atap tabung

Rumus yang berlaku pada bangun ruang tabung:

Luas permukaan:
L = 2πr(r + t)

Volume:
V = πr² t

Keterangan:
r = jari-jari alas
t = tinggi
π =  = 3,14

Contoh Soal & Pembahasan Bangun Ruang Tingkat SD

1. 6
2. 8
3. 10
4. 12

PEMBAHASAN :
Sifat-sifat kubus yaitu memiliki:

• 12 rusuk yang sama panjang
• 6 sisi yang berbentuk persegi
• 8 titik sudut
• 12 diagonal sisi/bidang
• 4 diagonal ruang
• 3 pasang bidang yang sama, sejajar, dan sebangun

Jawaban D

1. 1
2. 2
3. 3
4. 4

PEMBAHASAN :
Salah satu sifat dari kerucut adalah memiliki 2 sisi yang terdiri atas: 1 sisi alas berbentuk lingkaran dan 1 selimut (bidang lengkung) yang mengerucut ke titik puncak.
Jawaban B

1. 5
2. 8
3. 10
4. 15

PEMBAHASAN :
Gambar bangun ruang di atas adalah limas segilima. Sifat-sifat limas segilima sebagai berikut:

• Memiliki 6 sisi, 1 sisi alas dan 5 sisi tegak
• Memiliki 6 titik sudut, 1 titik sudut puncak dan 5 titik sudut pada alasnya
• Memiliki 10 rusuk

Jawaban C

1. Balok dan kubus
2. Tabung dan kerucut
3. Tabung dan bola
4. Limas segiempat

PEMBAHASAN :
Yang termasuk jenis prisma segiempat adalah kubus dan balok, karena memiliki bentuk yang serupa dengan balok dan kubus. Prisma segiempat memiliki alas berbentuk persegi dengan empat sisi dan memiliki selimut yang berbentuk segiempat.
Jawaban A

1. 11 cm
2. 12 cm
3. 13 cm
4. 14 cm

PEMBAHASAN :
V kotak = 1.728 cm³
Volume kubus = s³

Maka panjang rusuk kubus dapat dihitung sebagai berikut:
V = s³
s =
=
= 12 cm
Jawaban B

1. Kubus dan balok
2. Prisma segiempat
3. Bola dan tabung
4. Kerucut dan limas

PEMBAHASAN :
Titik sudut merupakan perpotongan tiga buah rusuk sedangkan rusuk merupakan  perpotongan dua buah bidang yang berbentuk garis. Bangun ruang yang tidak memiliki rusuk adalah tabung dan bola karena sisinya berbentuk lengkungan. Sehingga tabung dan bola tidak memiliki sudut.
Jawaban C

1. 3.123
2. 2.197
3. 3.287
4. 2.413

PEMBAHASAN :
Panjang rusuk (s) = 13 cm
Maka volume kubus dapat dihitung sebagai berikut:
V = s³ = s x s x s
= 13 cm x 13 cm x 13 cm
= 2.197 cm³
Jawaban B

PEMBAHASAN :
AB = 18 cm
BC = 12 cm
BF = 10 cm

Maka volume bangun ruang tersebut dapat dihitung sebagai berikut:
Bangun ruang tersebut adalah balok, maka rumus yang berlaku adalah v = p x l x t
V = 18 cm x 12 cm x 10 cm
= 2.160 cm³
Jawaban B

PEMBAHASAN 
Panjang (p) = 24 cm
Lebar (l) = 18 cm
Tinggi (t) = 14 cm

Maka luas permukaan balok dapat dihitung sebagai berikut:
L = 2 {(p x l) + (p x t) + (l x t)}
= 2{(24 cm x 18 cm) + (24 cm x 14 cm) + (18 cm x 14 cm)
= 2(432 cm² + 336 cm² + 252 cm² )
= 2 x 1.020 cm²
= 2.040 cm²
Jawaban A

Sebuah galon berbentuk tabung dengan tinggi = 50 cm dan jari-jari = 21 cm (π =  ). Galon tersebut hanya diisi  bagian saja. Maka volume isi tabung tersebut adalah …

1. 905 cm³
2. 950 cm³
3. 975 cm³
4. 61.075 cm³

PEMBAHASAN :
Diketahui:
t = 50 cm
r = 21 cm
π =
Isi galon =  bagian

Menentukan volume galon sebagai berikut:
Volume tabung = v = πr² t
V =  x (21 cm)² x 50 cm
=  x 22.050 cm³
= 69.300 cm³
Maka volume isi galon =  x 69.300 cm³ = 51.975 cm³
Jawaban C

1. 500 cm³
2. 600 cm³
3. 700 cm³
4. 800 cm³

PEMBAHASAN :
Diketahui:
AD = tinggi prisma = 20 cm
AC = tinggi segitiga (alas prisma) = 10 cm
BC = alas segitiga (alas prisma) =  8 cm

Bangun ruang di atas adalah prisma segitiga, maka volume prisma segitiga dapat dihitung sebagai berikut:
V = L_a  x t
L_a = luas alas , alas prisma adalah segitiga siku-siku
L_a = ½ x  alas segitiga x tinggi segitiga
= ½ x 8 cm x 10 cm
= ½ x 80 cm²
= 40 cm²

Maka volume prisma adalah:
V = 40 cm² x 20 cm
= 800 cm³
Jawaban D

1. 14.130 dm³
2. 12.100 dm³
3. 13.230 dm³
4. 15.160 dm³

PEMBAHASAN :
Diketahui:
r = 15 dm
π = 3,14

Bangun ruang tersebut adalah bola, maka rumus yang berlaku adalah:
V =  πr³
=  x 3,14 x 15 dm x 15 dm x 15 dm
=  x 10.597,5 dm³
= 14.130 dm³
Jawaban A

1. 320
2. 480
3. 520
4. 560

PEMBAHASAN :
Diketahui:
AB = p = 14 cm
BC = l = 10 cm
OP = t = 12 cm

Bangun ruang tersebut adalah limas segiempat maka volumenya dapat dihitung sebagai berikut:
V =  x (L_a x t)
L_a = luas alas = p x l
V = x (p x l) x t
=  x 14 cm 10 cm x 12 cm
=  x 1.680 cm³
= 560 cm³
Jawaban D

1. 876,2 cm²
2. 816,4 cm²
3. 516,5 cm²
4. 798,4 cm²

PEMBAHASAN :
Diketahui:
r = 10 cm
s = 16 cm
t = 14 cm
π = 3,14

Luas permukaan kerucut dapat dihitung sebagai berikut:
L = πr(r + s)
= 3,14 x 10 cm x ( 10 + 16) cm
= 31,4 cm x 26 cm
= 816,4 cm²
Jawaban B

1. 1.123 cm³
2. 1.432 cm³
3. 1.575 cm³
4. 1.625 cm³

PEMBAHASAN :
Bangun ruang di atas terdiri dari kubus dan balok
Kubus:
s = 7 cm
v = s³ = s x s x s
= 7 cm x 7 cm x 7 cm
= 343 cm³

Balok:
p = 8 cm
l = 7 cm
t = 22cm
v = p x l x t
= 8 cm x 7 cm x 22 cm
= 1.232 cm³

Maka volume gabungan = volume kubus + volume balok
= 343 cm³ + 1.232 cm³
= 1.575 cm³
Jawaban C

1. 350
2. 450
3. 550
4. 650

PEMBAHASAN :
Diketahui:
p = 15 m
l = 10 m
t = 3 m

Kolam ikan tersebut berbentuk balok, sehingga volumenya dapat dihitung sebagai berikut:
V  = p x l x t
= 15 m x 10 m x 3 m
= 450 m³
Jawaban B

1. 654
2. 785
3. 815
4. 765

PEMBAHASAN :
Diketahui:
r = 5 cm
t = 10 cm
π = 3,14

Volume tabung dapat dihitung sebagai berikut:
V = πr² t
= 3,14 x 5 cm x 5 cm x 10 cm
= 3,14 x 250 cm³
= 785 cm³
Jawaban B

PEMBAHASAN :
Diketahui:
r = 7 cm
t = 18 cm
π =

Maka volume kerucut dapat dihitung sebagai berikut:
V = x πr²t
=  x  x 7 cm x 7 cm x 18 cm
=  x  x 882 cm³
= 924 cm³
Jawaban C

PEMBAHASAN 
Diketahui:
Ukuran balok
Panjang (p) = 24 cm
Lebar (l) = 14 cm
Tinggi (t) = 16 cm
V = p x l x t
= 24 cm x 14 cm x 16 cm
= 5.376 cm³

Ukuran setengah tabung
r = ½ x 14 cm = 7 cm
t = 24 cm
V = πr² t
V = ½(πr² t)
= ½ x ( x 7 cm x 7 cm x 24 cm)
= ½ x ( x 1.176 cm³ )
= 1.848 cm³

Maka volume bangun ruang gabungan adalah:
V = volume balok + volume setengah tabung
= 5.376 cm³  + 1.848 cm³
= 7.224 cm³
Jawaban A

Sebuah prisma segitiga memiliki volume 480 dan tinggi prisma 16 cm. Maka luas alas prisma adalah … .

PEMBAHASAN :
Diketahui:
Volume (V) = 480
Tinggi (t) = 16 cm
Berlaku rumus: V = La x t

Maka luas alas prisma dapat dihitung sebagai berikut:


= 30 cm
Jawaban A

PEMBAHASAN :
Diketahui:
Diameter alas = 28 dm
Jari-jari alas (r) = x 28 dm = 14 dm
Tinggi (t) = 32 dm
Berlaku rumus:
Dengan

Maka volume penampungan air dapat dihitung sebagai berikut:



= 22 x 2 x 14 x 32
= 19.712
= 19.712 liter
Jawaban C

PEMBAHASAN :
Diketahui:
Secara umum, bangun ruang memiliki tiga unsur yang terdiri atas sisi, rusuk, dan titik sudut.
Jawaban B

PEMBAHASAN :
Prisma segienam: 8 sisi dan 18 rusuk
Kubus dan balok: 6 sisi dan 12 rusuk
Limas segienam: 7 sisi dan 12 rusuk
Limas segitiga: 4 sisi dan 6 rusuk
Jawaban A

Sebuah kardus berbentuk kubus memiliki panjang sisi 9 cm. Maka volume kardus tersebut adalah … .

PEMBAHASAN :
Diketahui:
Panjang sisi (s) = 9 cm
Berlaku rumus:

Maka volume kardus dapat dihitung sebagai berikut:

= s x s x s
= 9 cm x 9 cm x 9 cm
= 729
Jawaban D

PEMBAHASAN :
Bangun ruang adalah sebuah benda berbentuk tiga dimensi dan memiliki isi (volume). Contohnya adalah benda-benda berbentuk kubus, balok, prisma, limas, tabung, kerucut, dan bola.
Jawaban C