DAFTAR ISI
Rangkuman Materi Statistika Kelas 12
Perumusan Ukuran Statistika
Perumusan ukuran statistika dibedakan menjadi 2 jenis data, yaitu:
Data tunggal
Data yang diruliskan dengan mendaftar satu per satu
Data kelompok
Data yang dituliskan dengan bentuk interval kelas.
Ukuran Pemusatan
Ukuran statistik yang dapat menjadi pusat dari rangkaian data dan memberi gambaran singkat tentang data, terdiri dari tiga bagian yaitu mean, median dan modus
Mean (Rataan Hitung)
Merupakan ukuran pemusatan atau rata-rata hitung
Mean data tunggal
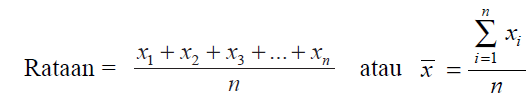
Keterangan:
∑x = jumlah data
n = banyaknya data
xi = data ke-i
Mean data distribusi frekuensi
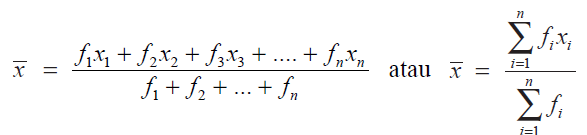
Keterangan:
fi = frekuensi untuk nilai xi
xi = data ke-i
Mean data kelompok
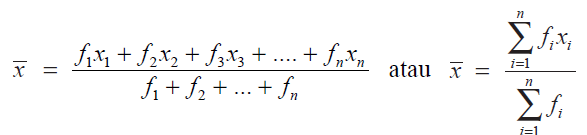
Keterangan:
fi = frekuensi untuk nilai xi
xi = titik tengah rentang tertentu
Cara lain:
- Menentukan rataan sementaranya.
- Menentukan simpangan (d) dari rataan sementara.
- Menghitung simpangan rataan baru dengan rumus berikut ini.
- Menghitung rataan sesungguhnya.
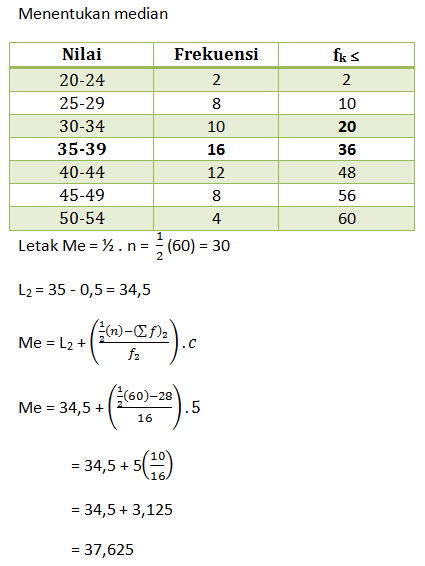
Median (Me)
Merupakan suatu nilai tengah yang telah diurutkan
Median data tunggal
Data ganjil: ambil nilai yang berada di tengah
Data genap: ambil rata rata dua data yang berada di tengah
Median data kelompok

Ket:
L2 = tepi bawah kelas median
n = banyak data
(∑f)2 = jumlah frekuensi sebelum kelas median
f2 = frekuensi kelas median
c = panjang interval kelas
Modus (Mo)
Merupakan nilai yang paling sering muncul atau nilai yang mempunyai frekuensi tertinggi
Modus data tunggal
Ambil data yang jumlahnya paling banyak
Modus data kelompok
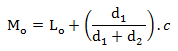
Ket :
L0= Tepi bawah kelas modus
d1= selisih frekuensi kelas modus dengan frekuensi kelas sebelum modus
d2= selisih frekuensi kelas modus dengan frekuensi kelas sesudah modus
c = panjang interval kelas
Ukuran Letak
Ukuran letak meliputi kuartil (Q), desil (D), dan Persentil (P).
Kuartil (Q)
Membagi data yang telah menjadi empat bagian yang sama banyak
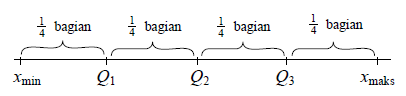
Keterangan:
xmin = data terkecil
xmaks = data terbesar
Q1 = kuartil ke-1
Q2 = kuartil ke-2
Q3 = kuartil ke-3
Kuartil data tunggal
![]()
Keterangan:
Qi = kuartil ke-i
n = banyak data
Kuartil data kelompok
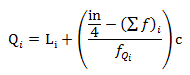
Keterangan:
Qi = kuartil ke-i (1, 2, atau 3)
Li = tepi bawah kelas kuartil ke-i
n = banyaknya data
(∑f)i = frekuensi kumulatif kelas sebelum kelas kuartil
c = lebar kelas
f = frekuensi kelas kuartil
Desil dan persentil
Desil membagi data menjadi sepuluh bagian yang sama besar. Sedangkan persentil membagi data menjadi 100 bagian yang sama.
Desil dan persentil data tunggal
Desil
![]()
Keterangan:
Di = desil ke-i
i = 1, 2, 3, . . ., 9
n = banyaknya data
Persentil
![]()
Keterangan:
Pi = persentil ke-i
i = 1, 2, 3, . . ., 99
n = banyaknya data
Ukuran Penyebaran
menggambarkan penyebaran data tersebut dan dapat dikaitkan dengan simpangan (lebar data) dari suatu nilai tertentu. Contoh : jangkauan, hamparan, simpangan, quartil, dan simpangan rata-rata
Jangkauan (J)
Selisih antara data terbesar dengan data terkecil
Jangkauan data tunggal
J = xmaks – xmin
Jangkauan data kelompok
J = nilai tengah kelas tertinggi – nilai tengah kelas terendah
Hamparan (Jangkauan antar kuartil) (R)
Selisih antara kuartil atas dengan kuartil bawah
Hamparan untuk data tunggal dan kelompok:
R = Q2 – Q1
Keterangan:
Q2 = kuartil atas
Q1 = kuartil bawah
Simpangan kuartil (Qd)
Simpangan antar kuartil
Simpangan antar kuartil untuk data tunggal dan kelompok:
Qd = (Q3 – Q1 )
Simpangan rata rata
Simpangan terhadap rata rata
Simpangan rata-rata data tunggal
![]()
Keterangan:
SR = simpangan rata-rata
n = ukuran data
xi = data ke-i dari data x1, x2, x3, …, xn
x = rataan hitung
Simpangan rata-rata data kelompok
Simpangan baku
akar dari jumlah kuadrat deviasi dibagi banyaknya data
Simpangan baku data tunggal
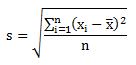
Keterangan: n = banyaknya data
Simpangan baku data kelompok
Ragam/Variasi
Ragam data tunggal

Keterangan: n = banyaknya data
Ragam data kelompok
![]()
Keterangan: n = banyaknya data
Contoh Soal Statistika, Pembahasan & Jawaban Kelas 12
Diberikan 7 data, setelah diurutkan, sebagai berikut: a, a+1, a+1, 7, b, b, 9. Jika rata-rata data tersebut 7 dan simpangan rata-ratanya
- 12
- 13
- 14
- 15
- 16
- 75
- 78
- 80
- 82
- 85
- 64,5
- 65
- 65,5
- 66
- 66,5
- 30
- 35
- 40
- 45
- 50
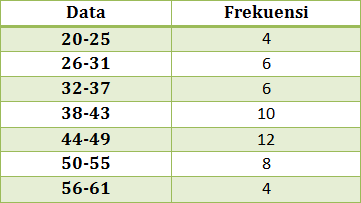
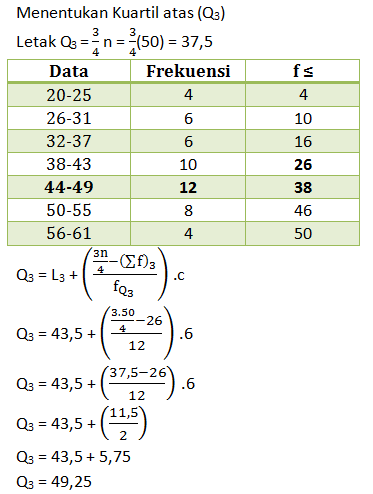
- 49,25
- 48,75
- 48,25
- 47,75
- 47,25
- 1/5
- 7/30
- 4/15
- 3/10
- 1/3
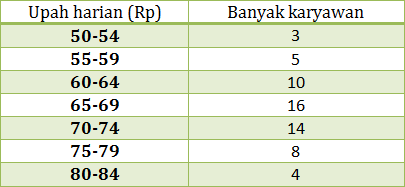
- 59,5
- 60,7
- 62,5
- 63,0
- 64,5
- 12%
- 15%
- 20%
- 22%
- 80%
PEMBAHASAN :
Jumlah Siswa dengan nilai 8 yaitu 22-19=3 siswa
Jumlah siswa = 25
Maka persentasinya = 3/25 x 100% =12%
Jawaban : A
- 32
- 37,625
- 38,25
- 43,25
- 44,50
- 24
- 27
- 30
- 33
- 36
- 3
- 4
- 5
- 6
- 7
- 6,33
- 6,50
- 6,75
- 7,00
- 7,25
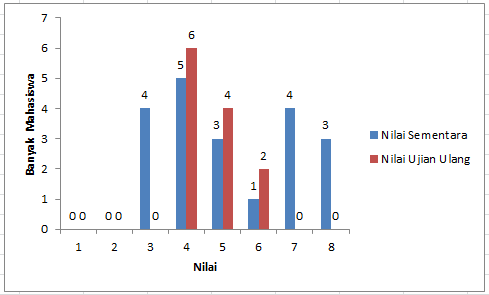
PEMBAHASAN :
Diketahui:
Jumlah mahasiswa yang lulus tanpa ujian ulang
Nilai 6 = 1 orang
Nilai 7 = 4 orang
Nilai 8 = 3 orang
Sedangkan mahasiswa yang lulus dengan ujian ulang
Nilai 6 = 2 orang
Jumlah mahasiswa yang lulus totalnya = 10 orang
Maka nilai rata-rata mahasiswa yang lulus baik tanpa ujian ulang atau dengan ujian ulang adalah:
![]()
Jawaban : D
- 5
- 7
- 9
- 11
- 14
PEMBAHASAN :
Diketahui:
p = banyak siswa yang memperoleh nilai < 7 atau mendapat nilai 6.
5 orang mendapat nilai = 7
Menentukan jumlah nilai untuk 30 siswa (∑ x30)
![]()
![]()
Maka ∑ x30 = 30 x 8 = 240
∑ x30 = 6p + 5.7 + (30-5-p)10
240 = 6p + 35 +(25-p)10
240 = 6p + 35 + 250 – 10p
240 – 285 = -4p
p = 45/4 = 11,25
Maka nilai yang mungkin paling besar adalah 11
Jawaban : D
PEMBAHASAN :
Menentukan rataan hitung
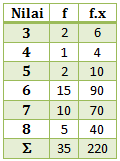
![]()
Menentukan median
Jumlah data/siswanya (n) = 35 (ganjil),
![]()
Mediannya nilai ke 18 jika diurut berdasarkan frekuensi maka nilai ke 18 adalah 5
Menentukan modus
Modus adalah nilai yang paling sering muncul atau frekuensinya paling banyak muncul. Maka modusnya yaitu nilai 6 sebanyak 15 kali
4, 2, 2, 5, 4, 5, 3, 3, 6
Tentukan jangkauan semi interkuartil
PEMBAHASAN :
Jangkauan semi interkuartil atau simpangan kuartil adalah setengah dari jangkauan kuartil
![]()
Menentukan Q1 dan Q3
dari data 4, 2, 2, 5, 4, 5, 3, 3, 6
![]()
Maka Q1 = 2
![]()
Maka Q3 = 3
Menentukan SQ
SQ = ½(Q3 – Q1) = ½ (3 -2) = ½
4,5, 6, 7, 3, 4, 5, 6, 3, 7, 3, 4, 5, 6, 7, 7, 5, 4, 6
PEMBAHASAN :
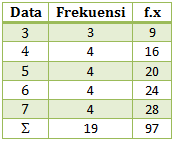
Menentukan rataan
![]()
Menentukan varians
![]()
![]()
![]()
varians = 1,88
Dalam satu sekolah jika diambil 3 kelas dan dihitung rata-rata nilai matematikanya. Kelas IPA 1, IPA 2 dan IPA 3 memiliki jumlah siswa 35, 32, 34 dan diketahui rata-rata gabungan nilai matematikanya adalah 54,3. Jika rata-rata nilai kelas IPA 1 adalah 45 dan rata-rata kelas IPA 2 adalah 65. Tentukan rata-rata nilai kelas IPA 3!
PEMBAHASAN :
Menentukan rata-rata nilai matematika kelas IPA 3 dari rata-rata gabungan
![]()
![]()
![]()
![]()
![]()
PEMBAHASAN :
Menentukan median
Median adalah nilai tengah, jika diurut berdasarkan frekuensi maka mediannya berada pada interval 33-35.
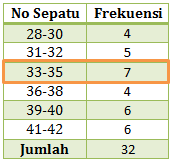
Diketahui:
tepi bawah (tb) = 32,5
panjang interval kelas (c) = 3
Jumlah data (n) = 32
Jumlah frekuensi sebelum kelas median (Σ fi) = 4 + 5 = 9
frekuensi median (fq) = 7
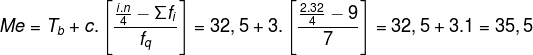
PEMBAHASAN :
Modus adalah data yang sering muncul. Jika dilihat dari frekuensi yang paling banyak. Maka modus ada pada interval: (33-35)
Diketahui:
tepi bawah (tb) = 32,5
panjang interval kelas (c) = 3
frek kelas modus – frek kelas sebelum = d1 = 7 – 5 = 2
frek kelas modus – frek kelas sesudah = d2 = 7 – 4 = 3
Menentukan Modus dengan rumusan
![]()
Mo = 33,7
PEMBAHASAN :
Karena titik tengah memiliki selisih = 3, maka panjang interval kelasnya (c) = 3. Kuartil atas berada pada titik tengah 49,1 berada pada interval 48-50.
Diketahui:
Q3 = 49,1
tepi bawah (tb) = 48,5
panjang interval kelas (c) = 3
banyaknya data (n) = 23 + x
Jumlah frekuensi sebelum kelas kuartil (Σ fi) = 20
Untuk menentukan nilai x ditentukan dari rumusan kuartil atas:

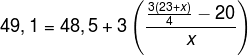
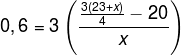
![]()
0,8x = 69 + 3x – 80
2,2x = 11
x = 5
PEMBAHASAN :
Diketahui:
Rata-rata awal ![]() = 42
= 42
jangkauan awal (J) = 9
Maka sesudah dikali x dan ditambah y maka nilainya menjadi
![]()
J = 9x + y = 19 ……pers (2)
Jika di eliminasi y, maka nilai x
33x = 66
x = 2
maka nilai y
9x + y = 19
9(2) + y = 19
18 + y = 19
y = 19 – 18 = 1
maka nilai 6x + y
6(2) + 1 = 13
- 15
- 25
- 35
- 45
- 55
PEMBAHASAN :
p + ½ (q + r) = 40 → kalikan dengan dua
2p + q + r = 80
q + ½ (p + r) = 50 → kalikan dengan dua
2q + p + r = 100
r + ½ (p + q) = 60 → kalikan dengan dua
2r + p + q = 120
4p + 4q + 4r = 300
4(p + q + r) = 300
p + q + r = 75
Maka rata-rata dari bilangan p, q, dan r = ![]() = 25
= 25
Jawaban : B
- a0 + 10
- a0 + 5
- a0 + 11
- a0 + 5,5
- a0 + 1
PEMBAHASAN :

Jawaban : D
- n(n + p + 4)
- n(n – p + 2)
- ½ n(n + p)
- n(n + p – 3)
- ½ n(n – p – 4)
PEMBAHASAN :

Jawaban : A
- 1 : 4
- 2 : 3
- 4 : 5
- 1 : 3
- 1 : 2
PEMBAHASAN :

Jawaban : E
- 9
- 7,9
- 9,5
- 8,25
- 7,5
PEMBAHASAN :
![]()
56 + 2x = 68
2x = 12
x = 6 → rata-rata nilai dua orang dengan nilai terbesar dan terkecil
xmax + xmin = 12
Selisih nilai terbesar dan terkecil = xmax – xmin = 4,5
2 . xmax = (12 + 4,5)
2 . xmax = 16,5
xmax = 8,25
Jawaban : D
Nilai | Frekuensi |
11-20 | 2 |
21-30 | 5 |
31-40 | 15 |
41-50 | 17 |
51-60 | 8 |
61-70 | 30 |
71-80 | 10 |
81-90 | 9 |
91-100 | 4 |
Jumlah | 100 |
Siswa yang lulus mendapatkan nilai 65,5. Maka banyak siswa yang lulus adalah …
- 27
- 32
- 38
- 41
- 45
PEMBAHASAN :
Misalkan a = jumlah siswa yang tidak lulus
Jumlah siswa = 100 orang
Tepi bawah (TB) = 61-0,5 = 60,5
Panjang kelas = c = 10
Frekuensi siswa yang lulus = f = 30
Nilai siswa yang lulus = 65,5

Maka banyak siswa yang lulus = 100 – 62 = 38
Jawaban : C
- Rata-rata dan jangkauan
- Rata-rata dan median
- Median dan simpangan kuartil
- Simpangan kuartil dan jangkauan
- Rata-rata dan simpangan kuartil
PEMBAHASAN :
Perhatikan tabel berikut ini!
| Data | Nilai data bertambah 5 | Perubahan |
| Rata-rata | Nilai data bertambah | |
| Median (Me) | M’e = Me + 5 | Nilai data bertambah |
| Simpangan kuartil (Sq) | S’q = Sq | Nilai data tetap |
| Jangkauan (J0) | J’ = J0 | Nilai data tetap |
Maka jika setiap nilai data ditambah 5, yang mengalami perubahan adalah rata-rata dan median.
Jawaban : B
- 8
- 2
- 10
- 4
- 5
PEMBAHASAN :
Rata-rata (![]() ) = 30
) = 30
Dikalikan a → ![]() ‘ = 30a
‘ = 30a
Dikurangi b → ![]() ” = 30a – b
” = 30a – b
Jangkauan (J) = 6
Dikalikan a → J’ = 6a
Dikurangi b → J” = 6a
Maka diperoleh persamaan sebagai berikut:
6a = 8 … (1)
30a – b = 40 … (2)
Substitusikan kedua persamaan di atas, yaitu:
6a = 8
![]()
30![]() a – b = 40
a – b = 40
40 – b = 40
b = 0
Maka nilai 6a + b = 6![]() – 0 = 8
– 0 = 8
Jawaban : A
- Rata-rata = 1000
- Jangkauan = simpangan kuartil
- Simpangan kuartil = 1012
- Modus = 1018
- Tidak ada yang berubah
PEMBAHASAN :
Data | Nilai data dikurangi 1000 |
| Jangkauan (J) | J’ = J |
| Rata-rata |
|
| Simpangan kuartil (Sq) | Sq’ = Sq |
| Modus (Mo) | Mo’ = Mo – 1000 |
Berdasarkan tabel di atas dapat disimpulkan sebagai berikut:
J’ = J = 30
Sq’ = Sq = 14
Mo’ = Mo – 1000
18 = Mo – 1000
Mo = 1018
![]() ‘ =
‘ = ![]() – 1000
– 1000
12 = ![]() – 1000
– 1000
![]() = 1012
= 1012
Jawaban : D
Ukuran | Frekuensi |
1 – 5 | 5 |
6 – 10 | 12 |
11 – 15 | 20 |
16 – 20 | 25 |
21 – 25 | 15 |
26 – 30 | 10 |
PEMBAHASAN :
Modus (Mo) adalah data yang paling sering muncul pada suatu data statistik.
Berlaku rumus sebagai berikut:

keterangan:
tb = tepi bawah kelas modus
d1 = selisih frekuensi kelas modus dengan kelas sebelumnya
d2 = selisih frekuensi kelas modus dengan kelas sesudahnya
c = panjang kelas
Ukuran | Frekuensi |
1 – 5 | 5 |
6 – 10 | 12 |
11 – 15 | 20 |
16 – 20 | 25 (Kelas Modus) |
21 – 25 | 15 |
26 – 30 | 10 |
d1 = 25 – 20 = 5
d2 = 25 – 15 = 10
c = 5
tb = 16 – 0,5 = 15,5

Jawaban : B
PEMBAHASAN :
Data = 5, 7, 5, 6, 7, 6
n = 6
Mencari rata-rata hitung sebagai berikut:

Rumus simpangan baku sebagai berikut:

Jawaban : A
Interval kelas | Frekuensi |
10 – 19 | 8 |
20 – 29 | 10 |
30 – 39 | 20 |
40 – 49 | 10 |
50 – 59 | 6 |
- 32,2
- 35,5
- 34,5
- 33,3
- 31,2
PEMBAHASAN :
Interval kelas | Frekuensi |
10 – 19 | 8 |
20 – 29 | 10 |
30 – 39 | 20 (kelas modus) |
40 – 49 | 10 |
50 – 59 | 6 |
![]()
d1 = 20 – 10 = 10
d2 = 20 – 10 = 10
c = 10
tb = 30 – 0,5 = 29,5

Jawaban : C
Nilai | Frekuensi |
45 – 49 | 5 |
50 – 54 | 8 |
55 – 59 | 10 |
60 – 64 | 6 |
65 – 69 | 12 |
Median dari data di atas adalah …
PEMBAHASAN :
Median adalah nilai tengah dari suatu data statistik. Rumus untuk median sebagai berikut:

Tb = tepi bawah kelas median = 49,5
n = banyak data = 40
f sebelum Me = frekuensi sebelum median = 5
f Me = frekuensi median = 8
I = jarak interval = 5
Nilai | Frekuensi | Frekuensi Kumulatif |
45 – 49 | 5 | 5 |
50 – 54 | 8 | 13 |
55 – 59 | 10 | 23 |
60 – 64 | 6 | 29 |
65 – 69 | 11 | 40 |
Total | 40 |

Jawaban : E
PEMBAHASAN :
Data: 3, 5, 7, 9, 11
n = 5
Menghitung rata-rata sebagai berikut:

Menghitung simpangan baku (S) sebagai berikut:

Jawaban : D
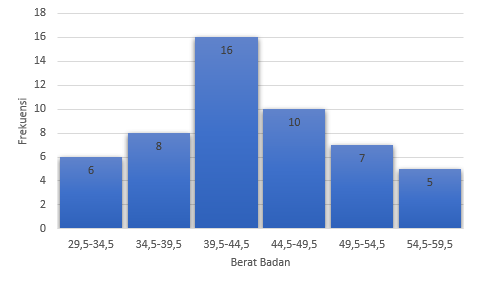
- 198,867
- 37,552
- 43,827
- 45,622
- 50,621
PEMBAHASAN :
Berat Badan | fi | Nilai (xi) tengah | fixi |
30 – 34 | 6 | 32 | 192 |
35 – 39 | 8 | 37 | 296 |
40 – 44 | 16 | 42 | 672 |
45 – 49 | 10 | 47 | 470 |
50 – 54 | 7 | 52 | 364 |
55 – 59 | 5 | 57 | 285 |
Total | 2279 | ||
Maka rata-rata hitung pada suatu daftar frekuensi sebagai berikut:
![]()
Keterangan:
fi = banyaknya data xi
xi = data pada kelompok ke-i
n = f1 , f2 , f3 , … , fn

Jawaban : C

- 11,9
- 21,8
- 23,5
- 40,2
- 35,6
PEMBAHASAN :
Tb | fi | xi | fixi |
4 – 14 | 5 | 9 | 45 |
14 – 24 | 10 | 19 | 190 |
24 – 34 | 8 | 29 | 232 |
34 – 44 | 2 | 39 | 78 |
Total | 25 | 545 |
Maka rata-rata dapat dihitung sebagai berikut:

Jawaban : B
Tinggi Badan (cm) | Frekuensi |
156 – 160 | 8 |
161 – 165 | 12 |
166 – 170 | P |
171 – 175 | 18 |
176 – 180 | 6 |
Total |
Jika median data di atas adalah 168,5 cm maka nilai P adalah …
- 20
- 32
- 28
- 40
- 50
PEMBAHASAN :
Diketahui:
Me = 168,5 cm
Tb = tepi bawah kelas median = 165,5
n = banyak data = 44 + P
∑f sebelum Me = frekuensi sebelum median = 20
f Me = frekuensi median = P
I = jarak interval = 5
Tinggi Badan (cm) | Frekuensi | Frekuensi Kumulatif |
156 – 160 | 8 | 8 |
161 – 165 | 12 | 20 |
166 – 170 | P | 20 + P |
171 – 175 | 18 | 38 + P |
176 – 180 | 6 | 44 + P |
Total | 44 + P |

Jawaban : A
- 5,1
- 6,0
- 4,1
- 4,5
- 5,3
PEMBAHASAN :
Diketahui:
Nilai rata-rata 30 orang = 7 → nilai total = 30 x 7 = 210
Nilai rata-rata dari 29 (tanpa nilai paling rendah) = 7,1 → 29 x 7,1 = 205,9
Maka nilai terendah = 210 – 205,9 = 4,1
Jawaban : C
Nilai Ujian | Frekuensi |
5 | 4 |
6 | 6 |
7 | 10 |
8 | 20 |
9 | 8 |
10 | 2 |
Siswa akan dinyatakan lulus jika nilainya sama dengan atau di atas rata-rata. Maka banyaknya calon yang lulus adalah … orang.
- 10
- 30
- 25
- 40
- 20
PEMBAHASAN :
Perhatikan tabel berikut ini:
Nilai Ujian (xi) | Frekuensi (f) | Xi .f |
5 | 4 | 20 |
6 | 6 | 36 |
7 | 10 | 70 |
8 | 20 | 160 |
9 | 8 | 72 |
10 | 2 | 20 |
Total | 50 | 378 |
Menghitung nilai rata-rata sebagai berikut:
![]()
Maka banyaknya yang lulus memiliki nilai >7,56 = 20 + 8 + 2 = 30 orang
Jawaban : B
PEMBAHASAN :
Data: 5, 7, 8, 5, 6, 10, 8, 6, 8, 7
n = 10
Menghitung nilai rata-rata sebagai berikut:

Maka simpangan baku dapat dihitung sebagai berikut:

Jawaban : A

- 35,55
- 42,67
- 34,94
- 45,05
- 30,5
PEMBAHASAN :
Diketahui:
Tb = 30,5
d1 = 18 -10 = 8
d2 = 18 – 8 = 10
I = 10

Jawaban : C

- 110
- 90
- 50
- 80
- 75
PEMBAHASAN :
Jumlah karyawan yang menyukai nasi goreng dapat dihitung sebagai berikut:
3600 – (600 + 900 + 300 + 1000) = 3600 – 2800 = 800

Jawaban : D

- 32
- 26
- 30
- 42
- 45
PEMBAHASAN :
Diketahui:
Jumlah siswa = 30 orang
2 + n + 6 + 8 + 10 + 26 = 56
n + 52 = 56
n = 56 – 52
n = 4
Maka banyak siswi yang lulus = 12 + 8 + 4 +2 = 26 siswi
Jawaban : B

- 32
- 26
- 30
- 42
- 45
PEMBAHASAN :
Diketahui:
Jumlah siswa = 30 orang
2 + n + 6 + 8 + 10 + 26 = 56
n + 52 = 56
n = 56 – 52
n = 4
Maka banyak siswi yang lulus = 12 + 8 + 4 +2 = 26 siswi
Jawaban : B
Nilai | Frekuensi |
50 – 54 | 2 |
55 – 59 | 3 |
60 – 64 | 8 |
65 – 69 | 12 |
70 – 74 | 6 |
75 – 79 | 4 |
Maka nilai rata-rata ulangannya adalah …
- 75,69
- 72,02
- 70,12
- 64,44
- 66,14
PEMBAHASAN :
![]()
Catatan:
xi = nilai tengah interval
Nilai | f | xi | f.xi |
50 – 54 | 2 | 52 | 104 |
55 – 59 | 3 | 57 | 171 |
60 – 64 | 8 | 62 | 496 |
65 – 69 | 12 | 67 | 804 |
70 – 74 | 6 | 72 | 432 |
75 – 79 | 4 | 77 | 308 |
Jumlah | 35 | 2315 |
Sehingga rata-rata nilai ulangan dapat dihitung sebagai berikut:

Jawaban : E
- 7,2
- 8,0
- 6,3
- 7,5
- 5,9
PEMBAHASAN :
Data statistika: 6, 5, 8, 6, 7, 4, 8, 4, 5, 7, 10, 5
Urutkan data menjadi: 4, 4, 5, 5, 5, 6, 6, 7, 7, 8, 8, 10
. Q1 Q2 = Me Q3
Maka nilai kuartil ketiga dapat dihitung sebagai berikut:
![]()
Jawaban : D
- 15
- 20
- 10
- 40
- 30
PEMBAHASAN :
Diketahui:
Misalkan banyak bilangan = n
Rata-rata = 30
Rata-rata sebenarnya = 32
Jumlah total bilangan = 30 x n = 30n
Jumlah nilai sebenarnya = 30n + 20
Menghitung rata-rata sebenarnya:

32n = 30n + 20
2n = 20
n = 10 → banyak bilangan
Jawaban : C
PEMBAHASAN :
Data: 6, 5, 7, 6, 4, 8
Menghitung rata-rata sebagai berikut:

Maka varian data dapat dihitung sebagai berikut:

Jawaban : D
- 71
- 69,1
- 65,8
- 74
- 55
PEMBAHASAN :
Misalkan:
Banyak siswa kelas P = nP = 35
Banyak siswa kelas Q = nQ = 25
Rata-rata ulangan Bahasa Inggris kelas P = ![]()
Rata-rata ulangan Bahasa Inggris kelas Q = ![]()
Rata-rata ulangan Bahasa Inggris gabungan = ![]() = 72
= 72

Jawaban : B
PEMBAHASAN :
Data statistik: a1, a2, a3, … , a10
Banyak data (n): 10
Pola data: ![]()
![]()
Dengan data mengikuti pola:
![]()
Maka rata-ratanya dapat dihitung sebagai berikut:

Jawaban : B

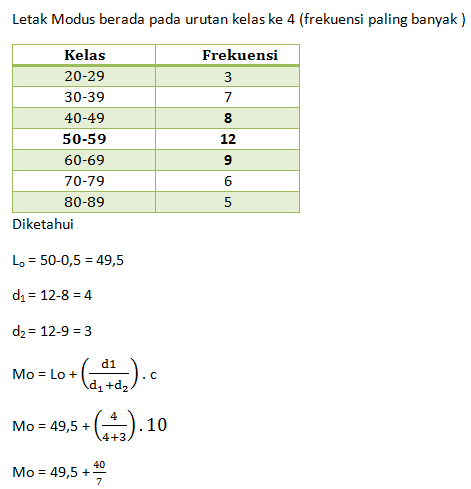
PEMBAHASAN :

tb = tepi bawah kelas modus = 40,5
i = panjang kelas = 10
Modus (Mo) adalah data yang paling sering/ banyak muncul pada suatu data statistika. Maka rumus yang dapat digunakan untuk menentukan modus sebagai berikut:

Jawaban : A
PEMBAHASAN :
Data = 8, 6, 8, 7, 5, 6, 7, 7
n = 8
Menentukan rata-rata hitung sebagai berikut:

Rumus simpangan baku sebagai berikut:

Jawaban : E

- 12,5
- 13,17
- 10,12
- 14,10
- 15,01
PEMBAHASAN :

Jawaban : B

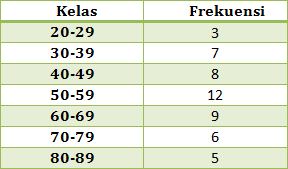
PEMBAHASAN :
Median adalah nilai tengah dari suatu data statistika.
Rumus untuk menentukan nilai median sebagai berikut:

Letak median = ½ x banyak data = ½ x 40 = 20
tb = tepi bawah kelas median = 39,5
n = banyak data = 40
Σf sebelum Me = frekuensi sebelum median = 10 + 5 = 15
f Me = frekuensi median = 12
i = jarak interval (panjang kelas) = 10

Jawaban : D
PEMBAHASAN :
Data statistika: 5, 7, 8, 6, 4
n = 5
Menentukan rata-rata hitung sebagai berikut:

Maka simpangan baku dapat dihitung sebagai berikut:

Jawaban : A
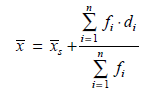

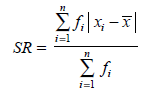
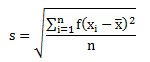
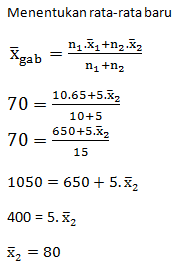
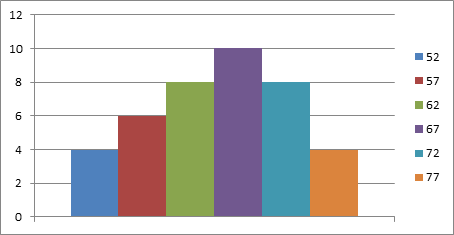
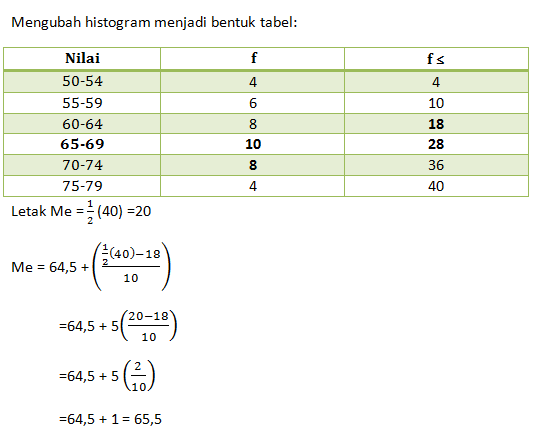

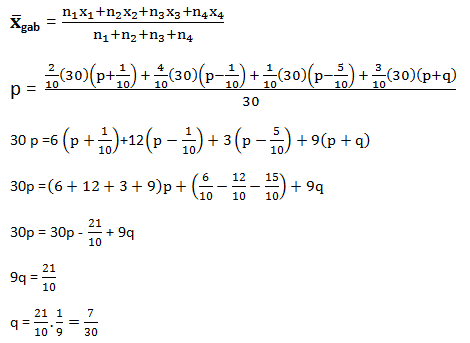
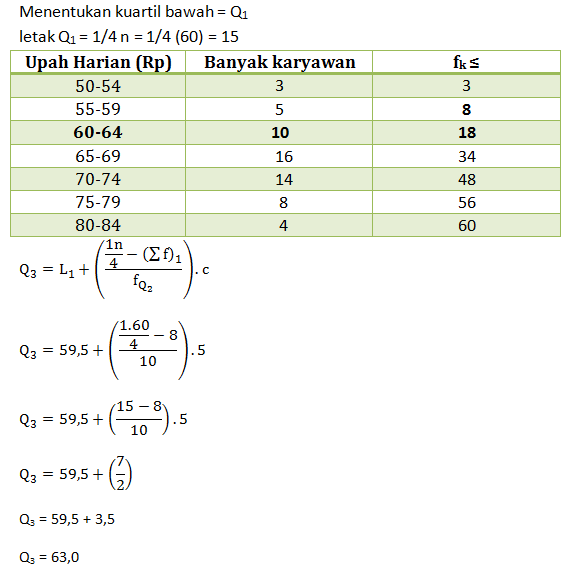



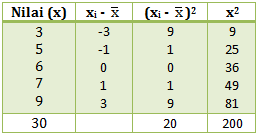
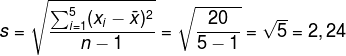
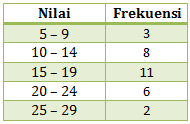

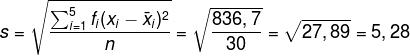
Permisi Izin Copas yang di atas yaa, buat tugas sekolah
Ada yg bisa bantu kah dg soal di bawah ini, trmksh
Diketahui dari sebuah penelitian terdapat jumlah populasi sebanyak 856, dan peneliti akan mengambil sampel sebanyak 150 orang. Peneliti akan menarik sampel secara sistematis, dan diketahui bahwa angka pertama yang terpilih sebagai sampel adalah responden nomer urut 10.
a. Tentukan nilai intervalnya
b. Tentukan 18 sampel berikutnya.
Terimakasih atas ilmunya